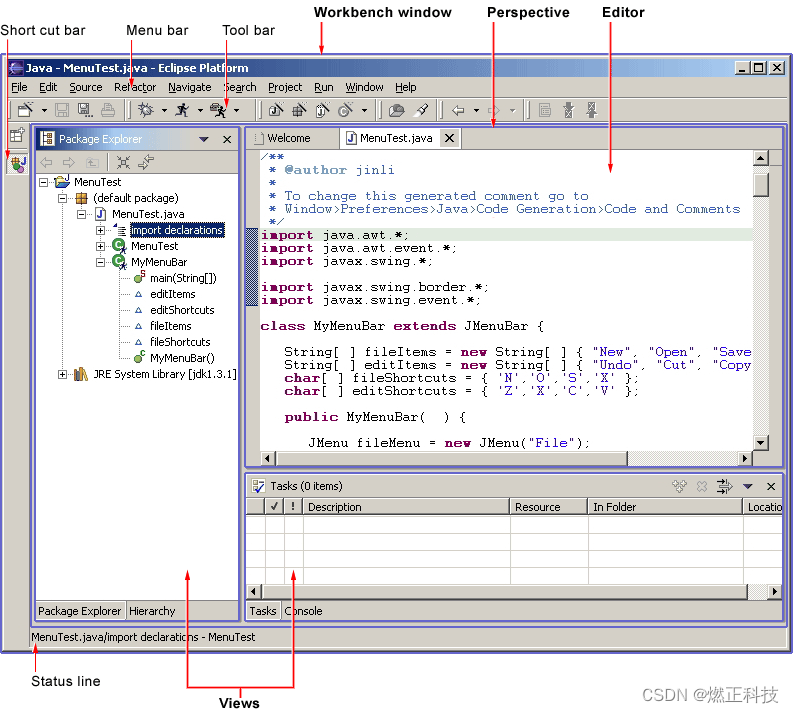
概念了解向，参考视频：

• 【小萌五分钟】机器学习 | 支持向量机 SVM

📚最大间隔分类器

• 如下图有两种不同颜色的点。我需要一个分类器告诉我，假设在下图中新加入一个点，应该将它分类至红点还是蓝点。
• 考虑加入一条决策边界，如果新加入的点落在它上方那就是红点，反之就是蓝点。问题就是这条边界怎么选？
  
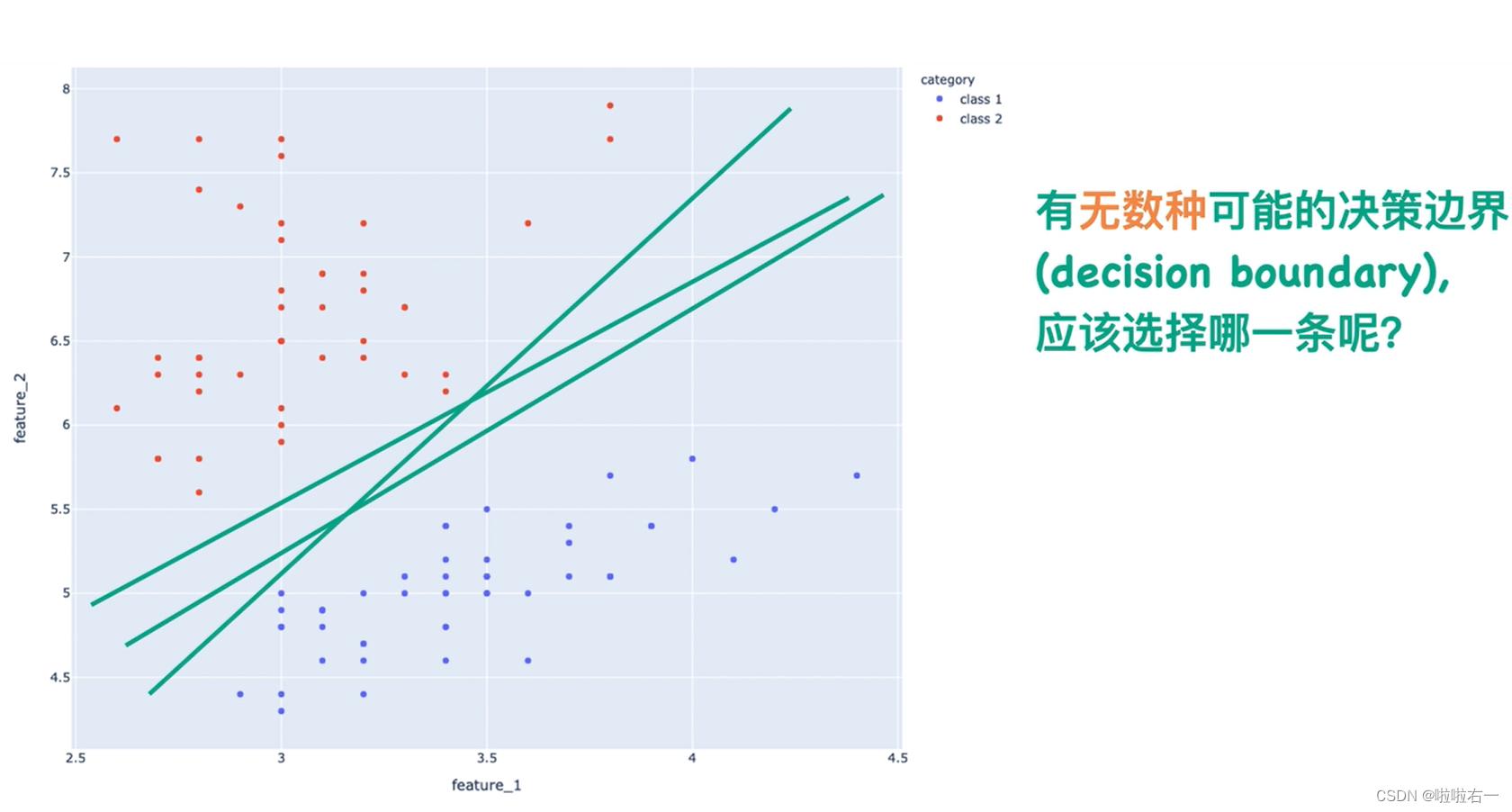
• 假设最终选定了一条，以下是相关补充概念：
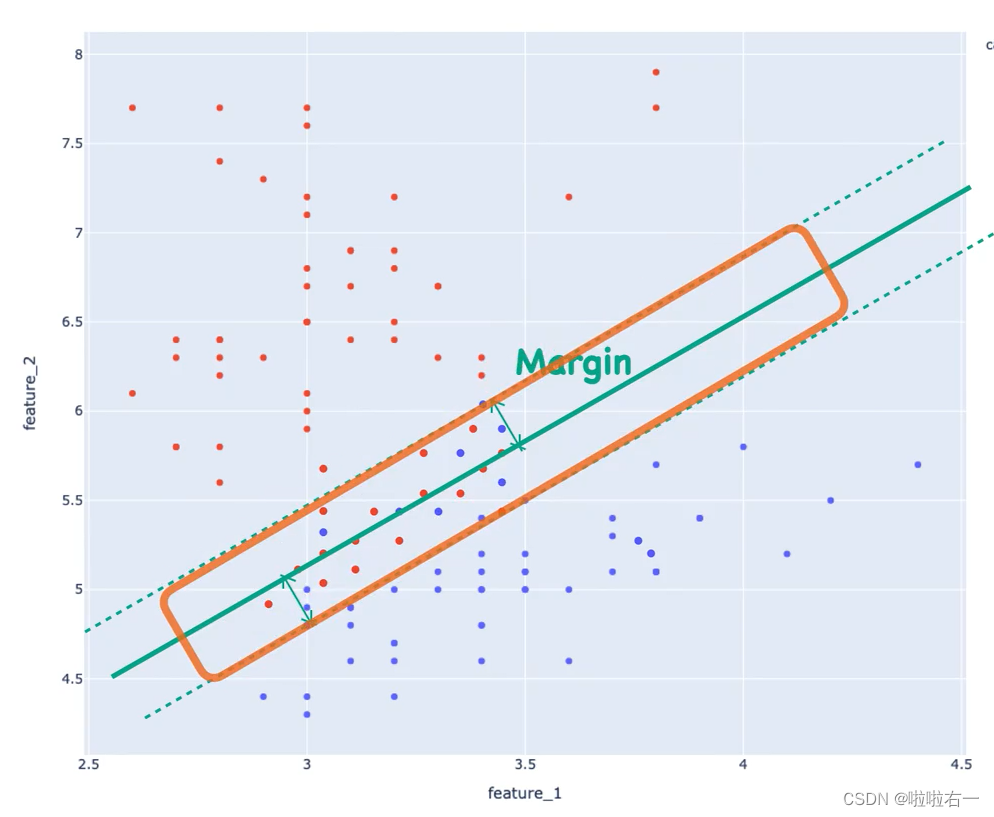
  • 支持向量：距离这条决策边界最近的点。
  • Margin：支持向量距离这条决策边界的距离。
• 假设这条决策边界的方程为：$y={\beta }_0+{\beta }_{1}x$，那么就可以知道任意点到这条决策边界的距离：
  
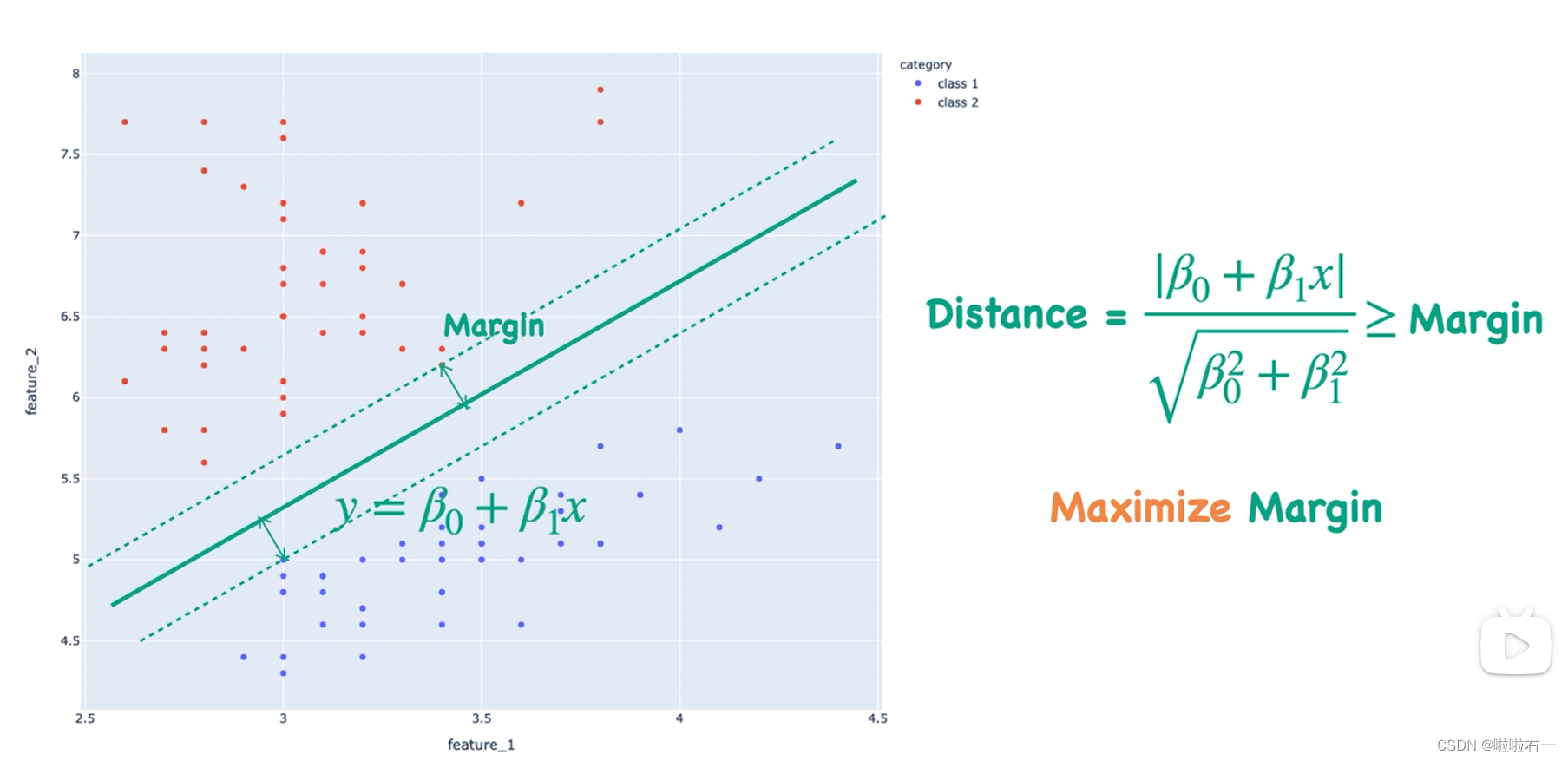
• 因为我们想要我们的模型尽量精确，所以现在要做的就是Maximize Margin，求得最大间隔分类器（Maximum Margin Classifier），这就是早期支持向量机的模型。
• 将上述公式扩展到多维并调整得到：
  
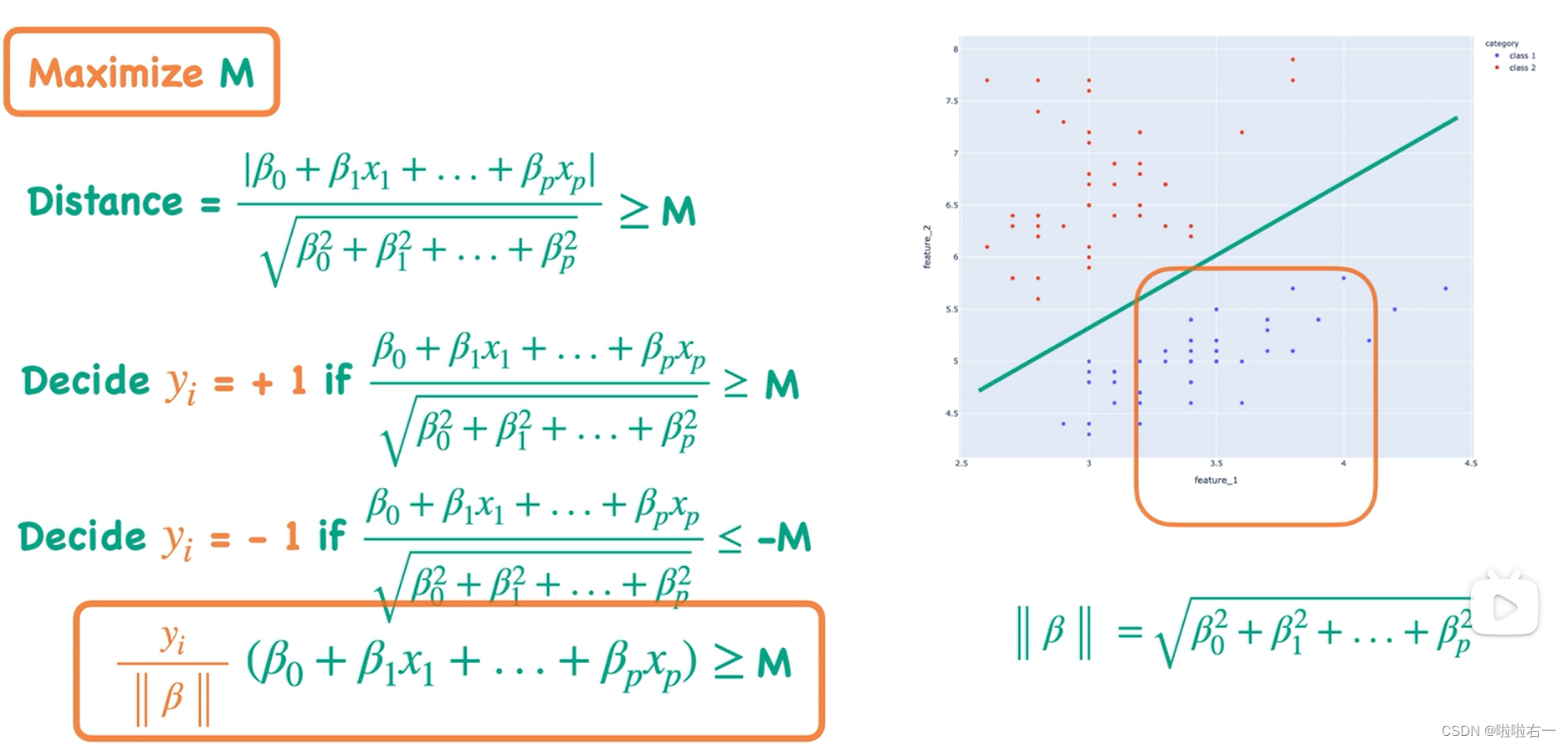
• 假令$M||\beta ||=1$，那就将问题转换为最小化$||\beta ||$。
  

---

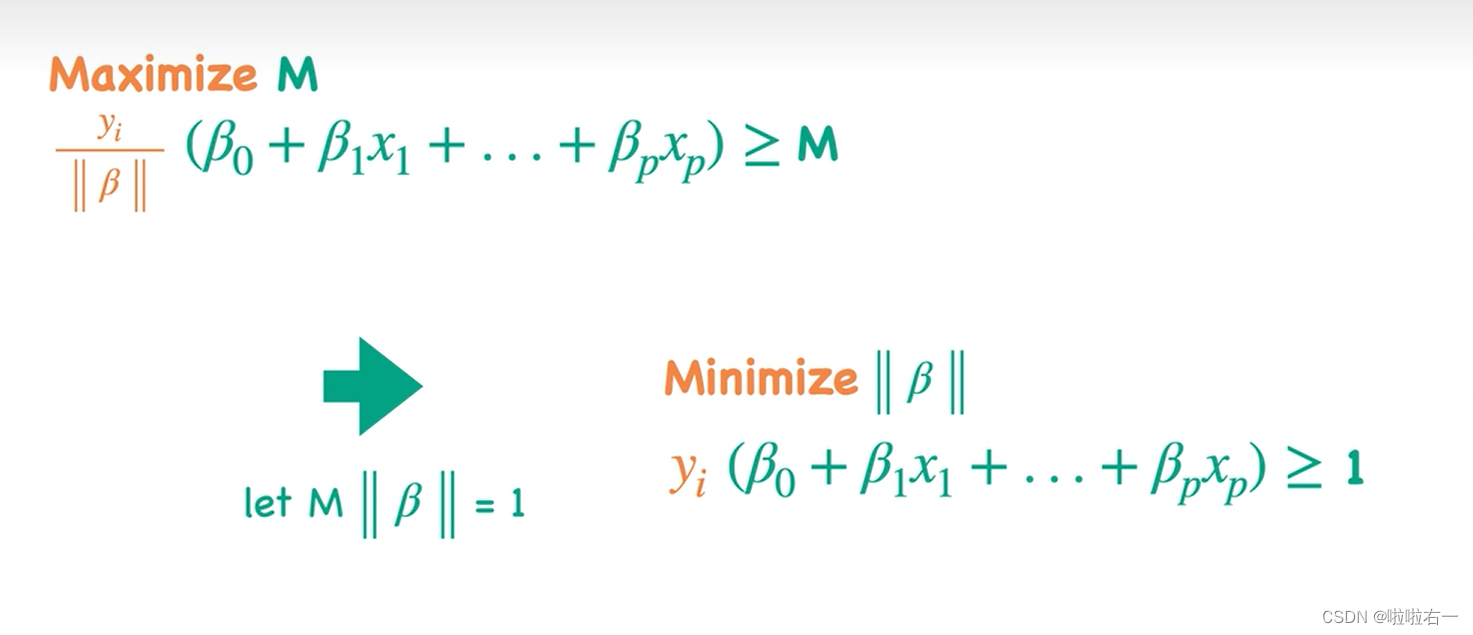
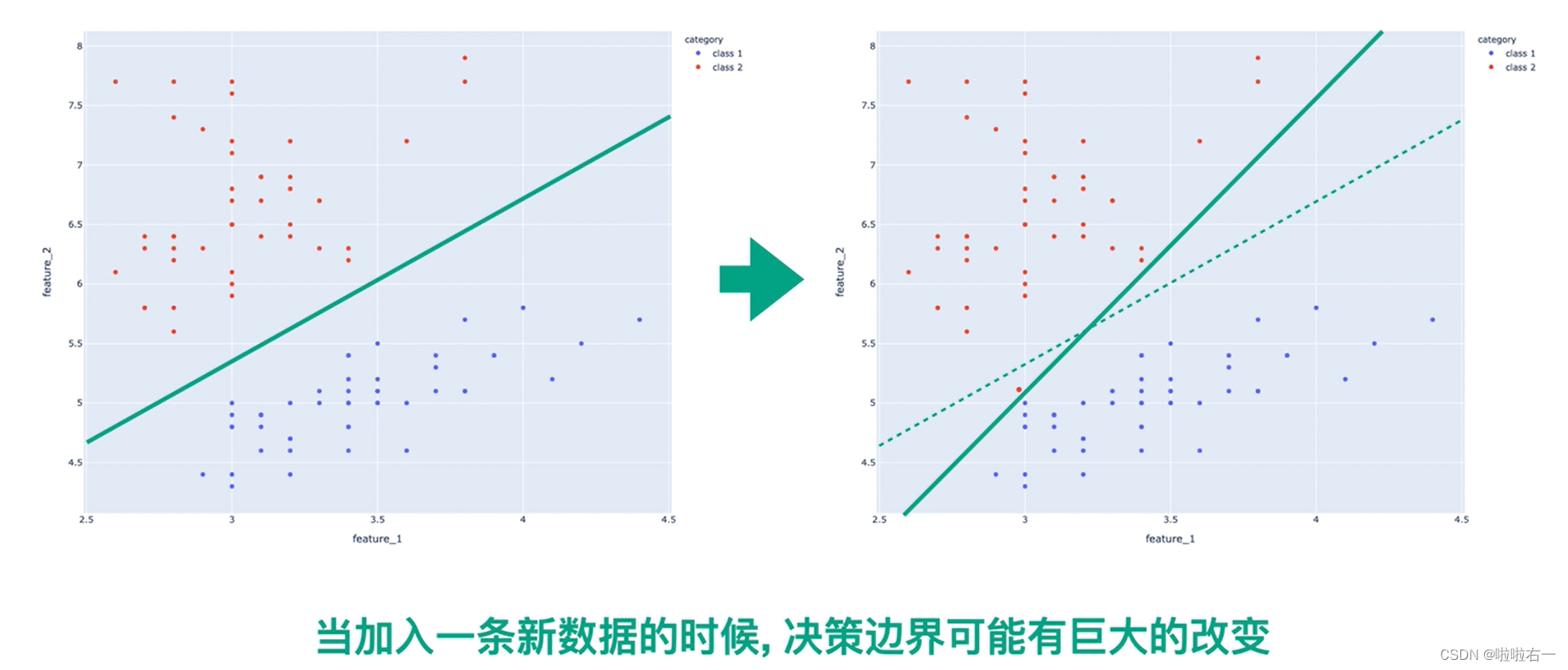
最大间隔分类器的缺陷：

• 当加入一条新数据的时候，决策边界可能有巨大的改变。
  
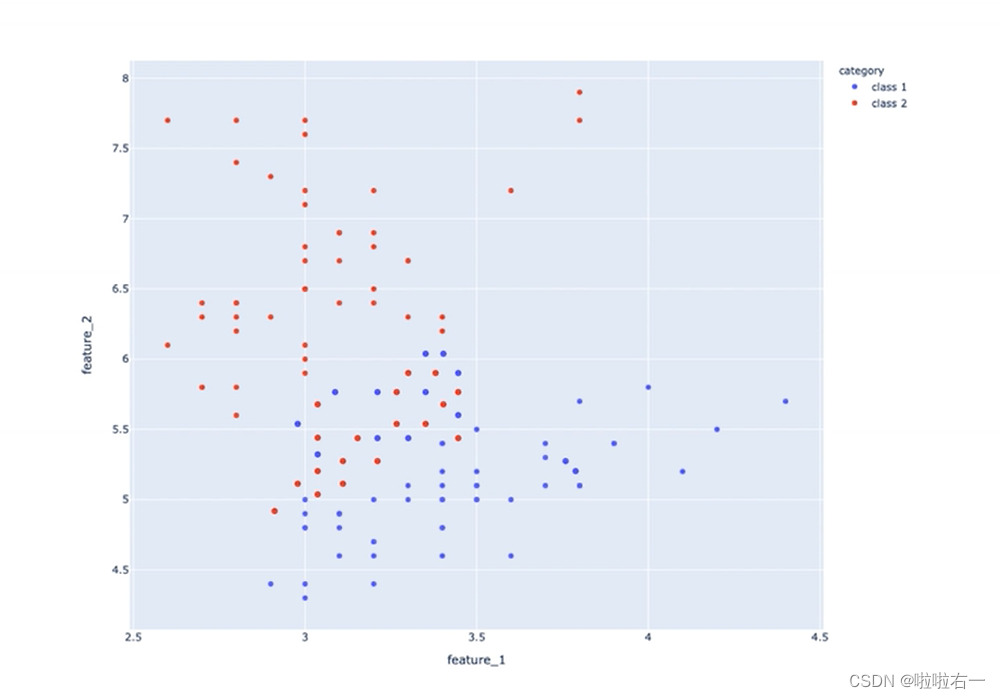
• 但数据线性不可分的时候，找不到决策边界。
  

📚软间隔分类器SVC

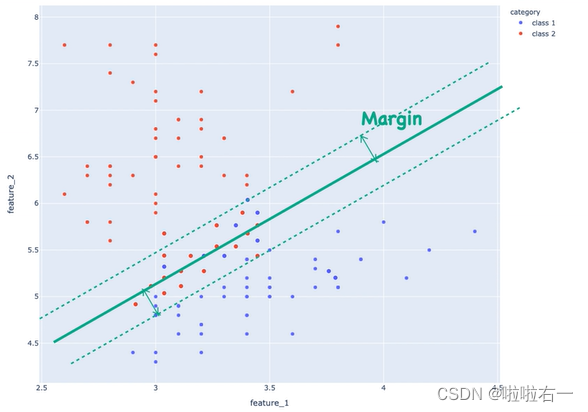
为了解决最大间隔分类器无法解决线性不可分的情况，我们考虑在原模型的基础上加一定的容忍度。从图像上看就是允许一部分点存在于虚线里面:

• 基于以上的想法，转化为公式即为设置一个松弛变量，该值取决于训练集中的第i个点。
  
• 针对这个C：当C特别大（margin越窄）的时候，容易出现过拟合；反之，当C特别小的时候，容易出现欠拟合。
  
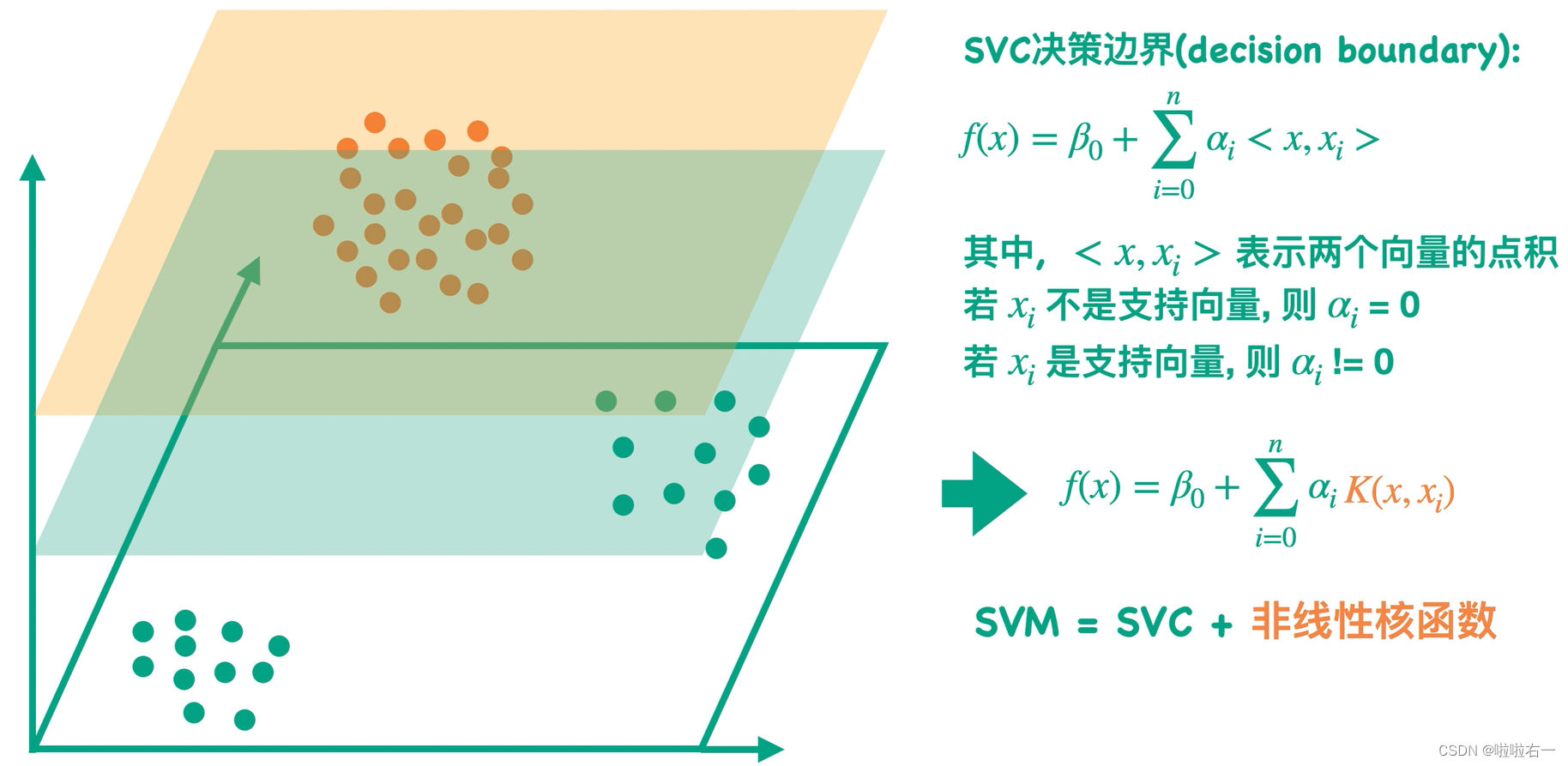
• 决策边界仅与支持向量有关

---

SVC决策边界

---

SVC模型的缺陷

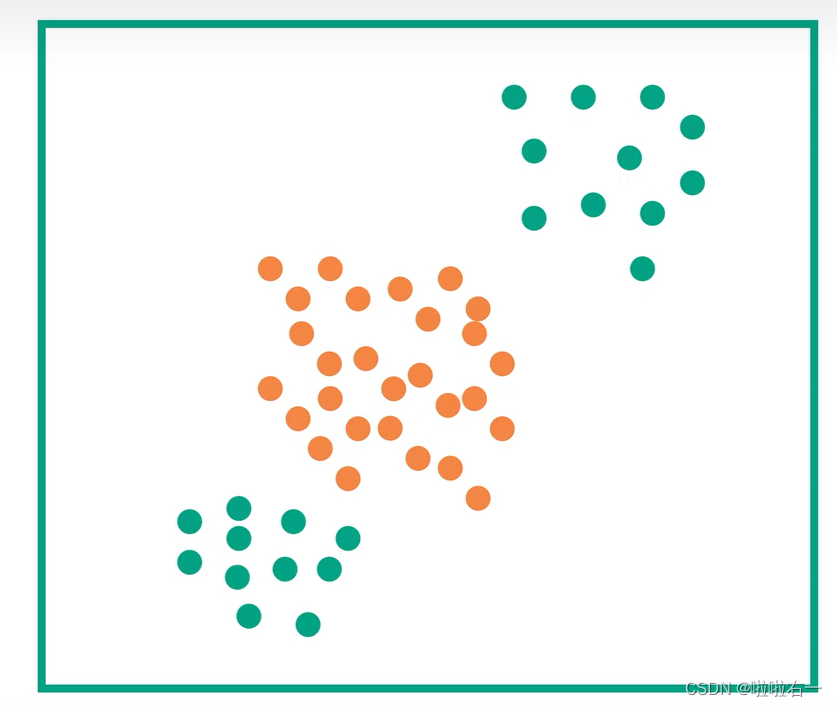
• 如下图实际上需要一条曲线作为决策边界，那SVC也无法解决
  

📚支持向量机SVM⭐️

🐇支持向量机是什么？

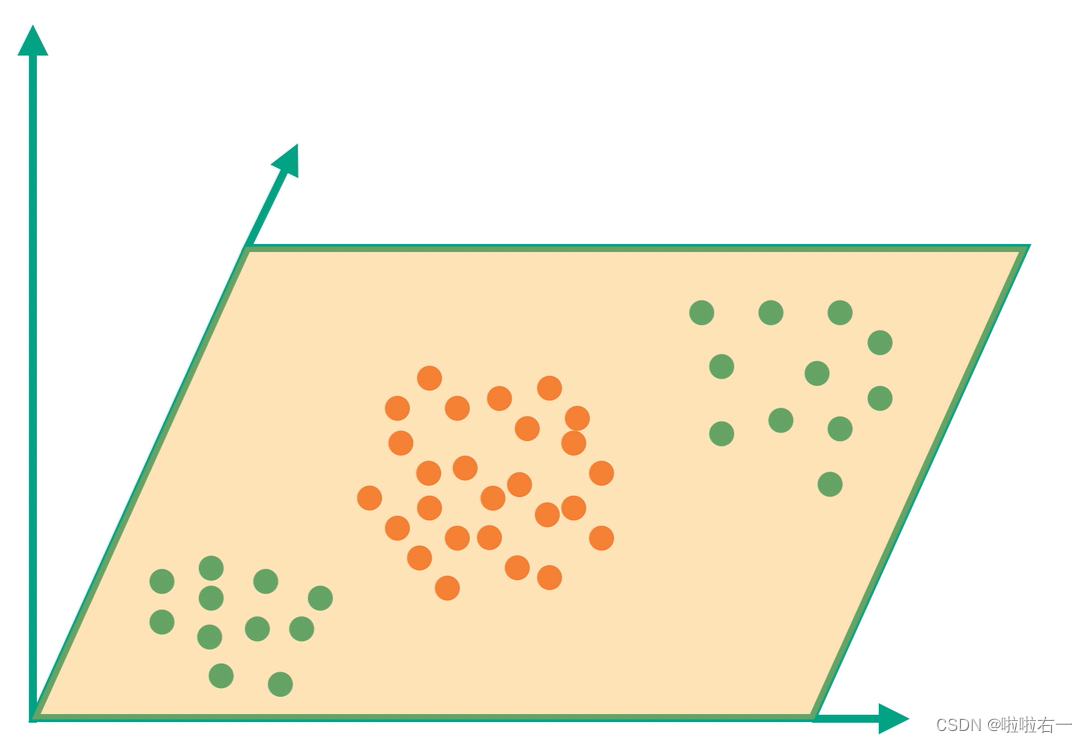
针对上边提到的SVC无法解决的情况，提出一种解决方法：增加一维
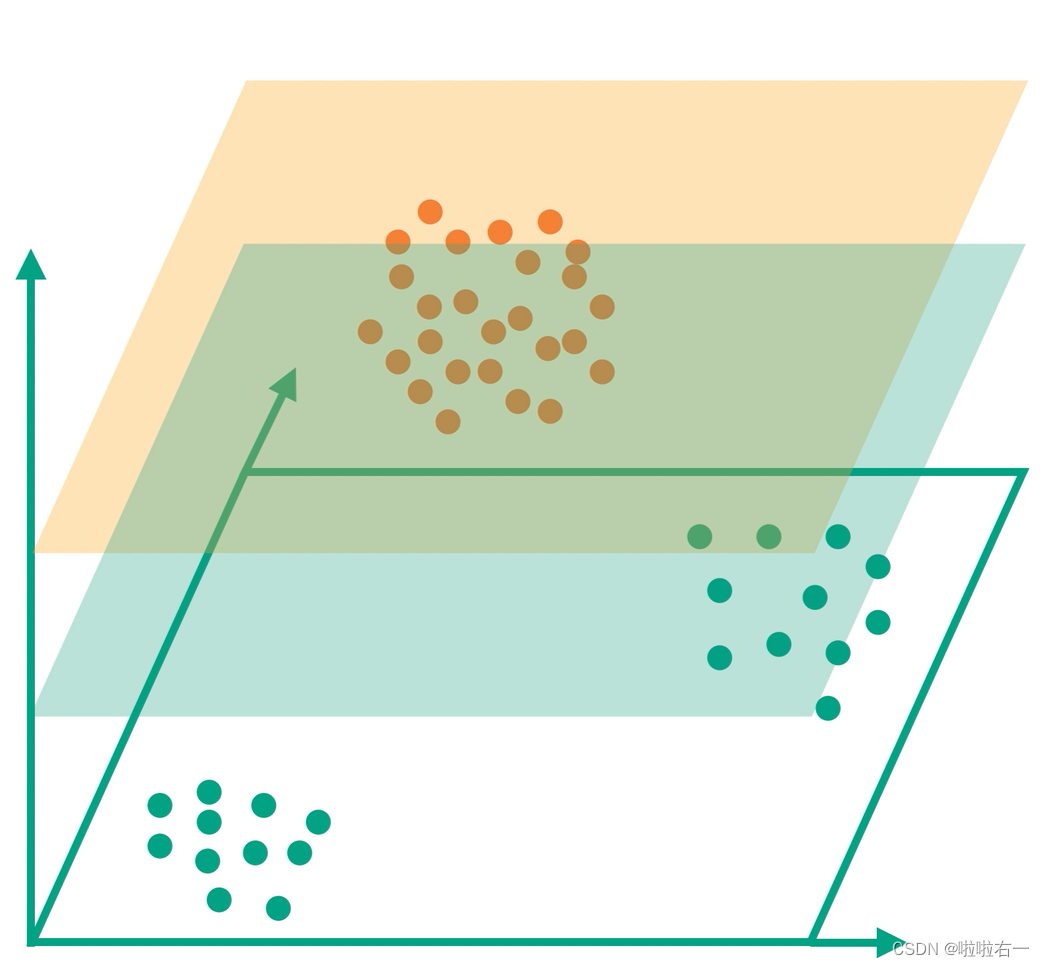
然后将橙色的那一堆点映射到另一个平面，然后找到一个中间平面实现分类：

---

• 引入Kernel Trick核技巧：SVM的本质是量化两类数据差异的方法，
  

---

AI创作助手：

• SVM（Support Vector Machine）是一种监督学习算法，用于分类和回归分析。
• SVM通过将训练数据映射到高维特征空间中，并寻找一个最优的超平面（即一个线性决策边界），将不同类别的数据进行分类。
• 该算法的目标是找到超平面，使得在该超平面上离它最近的样本点到该超平面的距离（即该点到超平面的“间隔”）最大化。
• SVM适用于二元分类和多元分类问题，也可以用于回归问题。
• 它的优点在于能够处理高维度的数据，具有较高的准确度，并且不容易受到噪音的影响。