前言
剑指offer专项突破版(力扣官网)——> 点击进入
本文所属专栏——>点击进入
一.字符串中的变位词
题目分析
- 总结
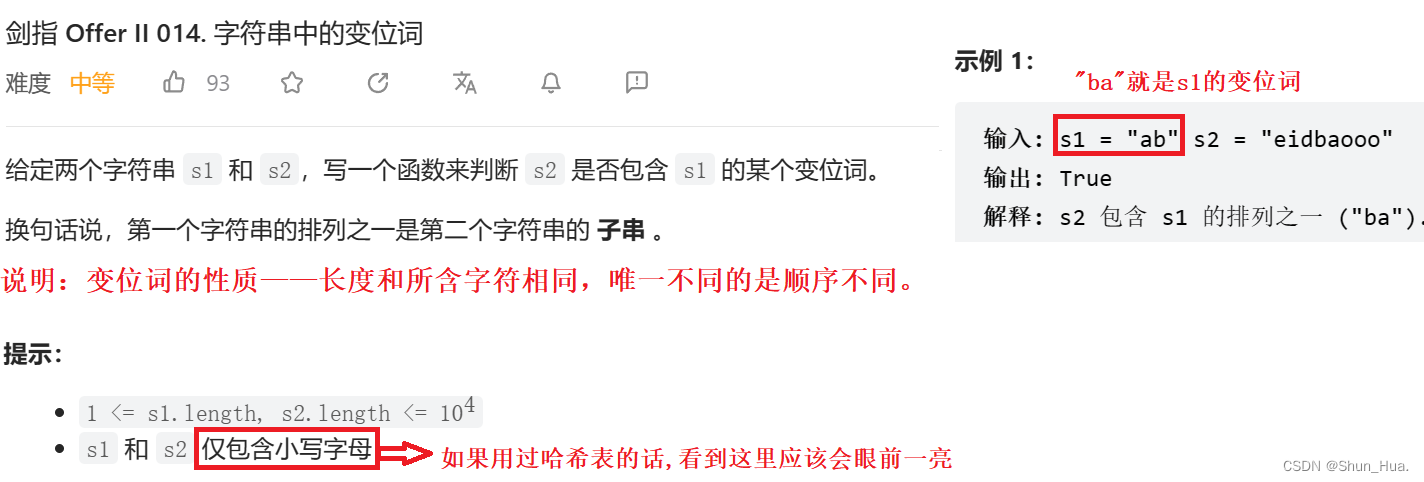
要求——在字符串2中找到字符串的1的排列顺序之一
数据格式——仅包含小写字母——哈希表!
返回值——bool值
思路分析
在分析这种情况的情况我们应该在脑中装上什么条件下s2的中包含s1的某个变位词!
当然是s2的长度大于等于s1的长度的情况下,那如果 s1的长度大于s2的长度就绝对不可能有这样的字符串 。
如果我们蛮力求解很容易放弃,因为s1排列组合为s1长度的阶乘,如果设s1的长度为n1的话,那么可能就会有n1! 种情况!这是一个很大的复杂度比2n次方还大!
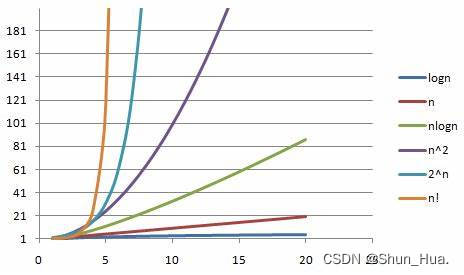
这主要是排列顺序提高了算法复杂度,如果我们消除这种排列顺序的影响,那么复杂度就会提升很多,那哈希表这种数据结构就派上了大用场,开辟一个数组arr(26个元素)用于存储26个字母出现的次数,那么在用上子串s1的长度不变,定义两个指针(确定查找的长度),先在让一个指针s2中移动s1个长度,并在s1中减上s2字符串中字符出现次数,此时如果能在s2中找到一种情况满足——arr中的元素全部为0,那么就找到了。如果还没有找到,那么就让左边的指针移动再把s1中的字符次数补上,右边的指针就再减上s1的字符出现的次数。这样直到找到或者右边的指针遇到s2的边界为止。
总结:这里的两个指针就好像一个在挣钱还债,一个在花钱负债,子串中的字符的出现次数就像是一个银行(存你原来有多少钱,其它位置没钱),那么当两个指针,达到这样的情况,刚好把你的原来的钱花完——arr中全部为0。
举个例子:

- 总结
第一步:判断是否s2的长度大于等于s1的长度(前提)
第二步: 开辟数组(26个元素),用于存储子串s1的字符出现次数。
第三步:固定长度——两个指针,一个右指针(欠钱)移动s1字符串的长度,一个左指针(还钱)。
第四步:第一次移动完之后,需要判断是否刚好没钱。
第五步: 如果判断还负债,则右指针继续欠钱,左指针继续挣钱。
第六步: 当找到时,或者右指针越界时,停止返回布尔值。
代码
bool is_zero(int *arr)
{
//当有不是0的情况就是有钱或者欠钱
for(int i = 0; i < 26; i++)
{
if(arr[i] != 0)
{
return false;
}
}
return true;
}
bool checkInclusion(char * s1, char * s2)
{
//前提s1的长度小于等于s2的长度
int len1 = strlen(s1);
int len2 = strlen(s2);
if(len1>len2)
{
return false;
}
//开辟并初始化一个数组,存储s1字符出现的次数
int *arr =(int*)malloc(sizeof(int)*26);
memset(arr,0,sizeof(int)*26);
for(int i = 0; i < len1; i++)
{
arr[s1[i]-'a']++;
}
//让右指针先花钱,花到s1的长度为止
for(int right = 0; right < len1; right++)
{
arr[s2[right]-'a']--;
}
//看这里是否刚好花完,没有负债。
if(is_zero(arr))
{
return true;
}
//如果还没有刚好花完,就继续移动
for(int right = len1,left = 0; right < len2;)
{
arr[s2[right++]-'a']--;
arr[s2[left++] -'a']++;
if(is_zero(arr))
{
return true;
}
}
//释放空间
free(arr);
arr = NULL;
return false;
}
二.字符串中的所有变位词
题目分析
- 总结
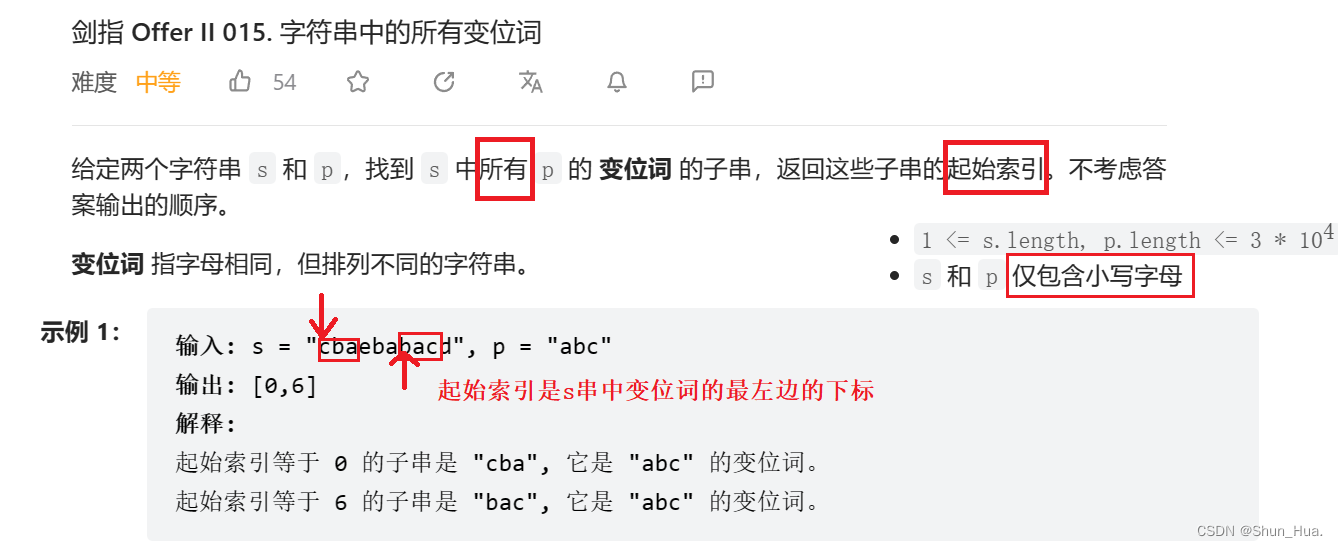
1.数据格式——26个小写字母组成的字符串——哈希
2.要求——找到所有变位词的子串,并记录起始的索引下标。
3.返回形式——数组——malloc
思路分析
跟上一题的思路基本一样,换汤不换药,不过我们需要自己开辟一个数组存起始位置的下标而已。
- 总结
第一步:判断是否s的长度大于等于p的长度(前提)
第二步: 开辟数组(26个元素),用于存储子串p的字符出现次数。
这里需要多一步的是,开辟一个数组——大小一次开够(s长度个元素)
第三步:固定长度——两个指针,一个右指针(欠钱)移动s字符串的长度,一个左指针(还钱)。
第四步:第一次移动完之后,需要判断是否刚好没钱,如果刚好没钱需要记录起始索引。
第五步: 如果判断还负债,则右指针继续欠钱,左指针继续挣钱。继续移动,有记录起始索引。
第六步: 右指针越界时,就停止循环。
代码
bool is_zero(int* arr)
{
for(int i = 0; i < 26; i++)
{
if(arr[i] != 0)
{
return false;
}
}
return true;
}
int* findAnagrams(char * s, char * p, int* returnSize)
{
int len_s = strlen(s);
int len_p = strlen(p);
//先开辟一个数组用于存储起始索引
int *apos = (int*)malloc(sizeof(int)*len_s);
*returnSize = 0;
//前提
if(len_p > len_s)
{
printf("hehe");
return apos;
}
//开辟数组存储子串信息
int *arr =(int*)malloc(sizeof(int)*26);
memset(arr,0,sizeof(int)*26);
for(int i = 0; i < len_p; i++)
{
arr[p[i]-'a']++;
}
//同时移动右指针,先花到len_p个长度
for(int right = 0; right < len_p; right++)
{
arr[s[right]-'a']--;
}
//判断一下是否刚好花完
if(is_zero(arr))
{
apos[(*returnSize)++] = 0;
}
//继续判断
for(int left = 0,right = len_p; right < len_s;)
{
arr[s[right++]-'a']--;
arr[s[left++]-'a']++;
if(is_zero(arr))
{
apos[(*returnSize)++] = left;
}
}
//记得释放空间
free(arr);
arr = NULL;
return apos;
}
三.不含重复字符的最长子字符串
题目分析
- 总结
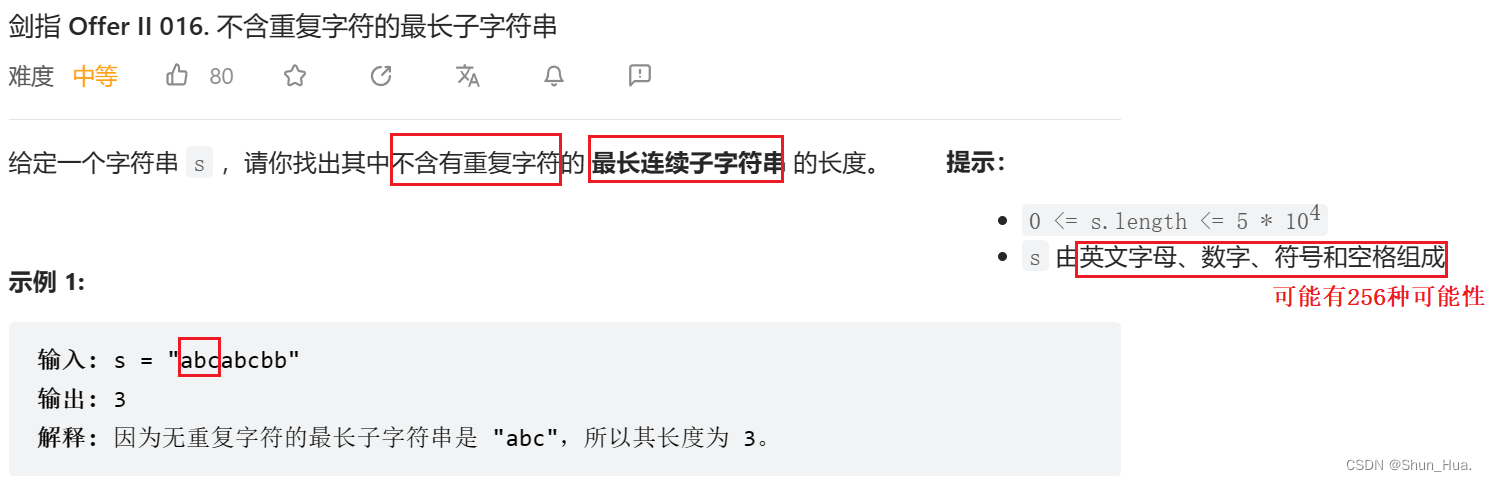
1.数据格式——最大可能有256个字符
2.要求找到——不含有重复字符的最长连续子字符串的长度
3.返回值——符合要求的长度
思路分析
既然是不含重复字符的长度,那么字符出现的次数就显得格外重要,那记录字符串出现的次数就还得用到哈希表,那么当字符在哈希表出现两次时,此时字符串中就含有相同字符。开始我们需要一个指针指向右边界,不断的在哈希表中加上字符出现的次数,这时指向左边界的指针不动,同时计算当前字符串的长度,直到某个字符在哈希表中出现两次,然后那么我们只需让左指针,调整到没有相同字符串为止。继续计算,直到右指针越界为止。
- 总结
第一步:开辟并初始化空间存储字符出现的信息
第二步: 让右指针,在数组中加到有重复字符为止,同时计算并比较得出当前最大长度。
第三步: 让左指针,在数组中不断去字符,直到去掉重复的字符为止。
代码
int lengthOfLongestSubstring(char * s)
{
//开辟空间,记录字符出现的次数
int *arr = (int*)malloc(sizeof(int)*256);
//初始化数组元素为0
memset(arr,0,sizeof(int)*256);
//所求最大长度
int max_len = 0;
//字符串长度
int len_s = strlen(s);
//计算思路
bool repeat = false;
for(int left = 0,right = 0; right < len_s;)
{
//先让数组中加到有重复元素为止。
while(right < len_s && !repeat)
{
arr[s[right++]]++;
//此时right已经加1了,因此我们要看的是上一个是否为2
if(arr[s[right-1]] == 2)
{
repeat = true;
break;
}
//此为不重复的字符串
//下标:左闭右开
int len = right - left;
if(len > max_len)
{
max_len = len;
}
}
//这里会出现重复数字,也可能是数组右指针越界
while(left < right && repeat)
{
if(arr[s[left]]==2)
{
repeat = 0;
}
arr[s[left++]]--;
}
}
return max_len;
}
四.含有所有字符的最短字符串
题目分析
- 总结
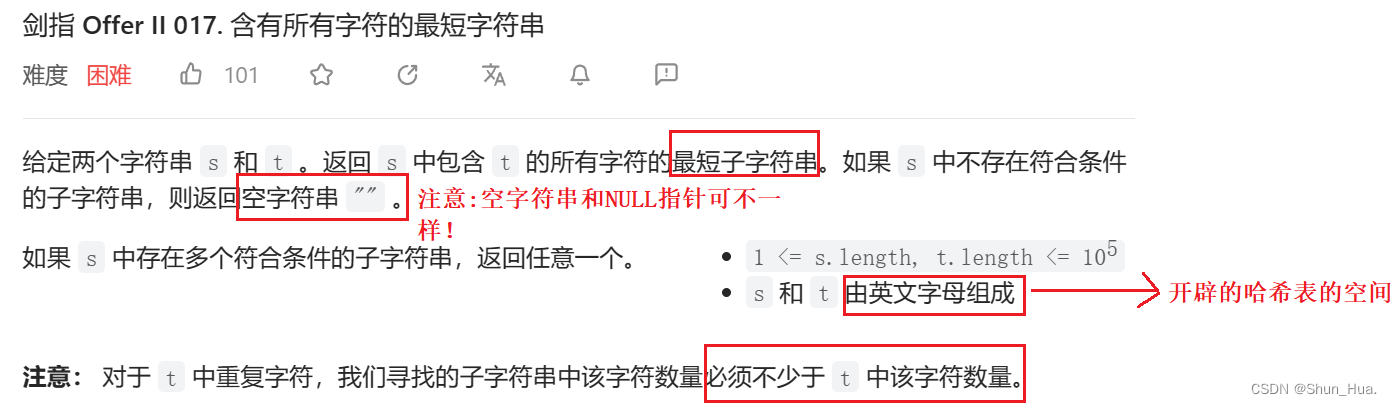
数据格式——英文字母
要求——包含子串的最小字符串
返回——符合要求的字符串
思路分析
思路大致与前几道相同,不过我们这里字符串的条件,最开始存的字符串都为0,即包含了子串的所有字符,其它的不用看,因此我们需要记住,这里的子串的字符的出现总次数就是子串的长度,如果访问到大于0的就是子串的字符,总次数就要减一,如果其它的则不用,直到总次数为0即可,总次数等于0,这时就要算长度比较,并且要让左边界进行调整,直到遇到有一个数,其次数哈希表中大于0,这是我们就跳过了一个子串的字符,使之又达到了不完整的状态,继续上面的动作,直到遇到右边界为止,这时又需要注意,当遇到右边界时,总次数也可能为0,还要进行判断!
- 总结
第一步:开辟空间存储字符串,记得也要给\0留位置。开辟空间存储字母出现的次数。
第二步:进行上述思路的计算。
第三步:拷贝字符串。
char * minWindow(char * s, char * t)
{
//求子符串长度
int len_s = strlen(s);
int len_t = strlen(t);
//为存储的字符串开空间
char* str = (char*)malloc(sizeof(char)*(len_s+1));//给\0留一个位置
memset(str,0,sizeof(char)*(len_s+1));
//为字符出现次数的信息开空间
int size = 'z'-'A' + 1;
int * arr = (int*)malloc(sizeof(int)*size);
memset(arr,0,sizeof(int)*size);
//算法思路
//存放字符的信息
for(int i = 0; i < len_t; i++)
{
arr[t[i]-'A']++;
}
//左边和右边的下标
int begin = 1;
int end = 0;//错开方便,判断最后没有的情况。
int min_len = len_s + 1;//跟它比永远小
int count = len_t;//子串字符出现的总次数
for(int right = 0,left = 0; right < len_s||(count==0&&right==len_s); )
{
if(count > 0)
{
arr[s[right]-'A']--;
if(arr[s[right]-'A'] >= 0)
{
count--;
}
right++;
}
else
{
int len = right - left;//左闭右开
printf("%d",len);
if(len < min_len)
{
begin = left;
end = right;//也是左闭右开
min_len = len;
}
arr[s[left]-'A']++;
if(arr[s[left]-'A'] > 0)
{
count++;
}
left++;
}
}
//拷贝字符串
for(int i = 0,left = begin; left < end; left++,i++)
{
str[i] = s[left];
}
free(arr);
arr = NULL;
return str;
}
五.有效的回文
题目分析
- 总结
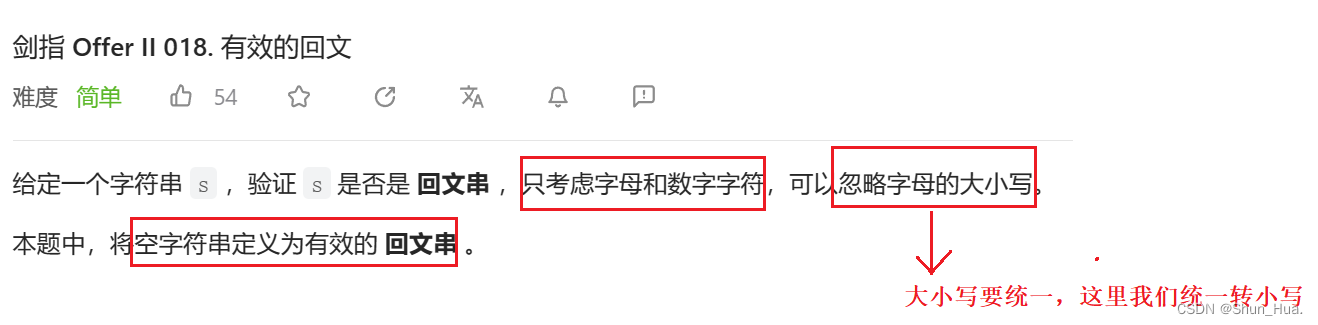
要求:只考虑字母和数字字符,大小写忽略
返回值:返回bool值
思路分析
这道题用双指针进行判断,是否是回文了,由于这道题难度不大,具体的思路就不说了,这里我们说几个细节,字符数组的开辟要留意给\0开辟空间,并且空字符串也是回文。
- 总结
第一步:将字符串的有效信息存储到为字符串开辟的空间中,并将大写字母转换成小写字母。
第二步:用双指针进行判断是否是回文。
代码
bool is_rsame(char* str1,int begin,int end)
{
while(begin <= end)
{
if(str1[begin]!=str1[end])
{
return false;
}
begin++;
end--;
}
return true;
}
bool isPalindrome(char * s)
{
int len = strlen(s);
//开辟空间存储字符串的信息
char* str = (char*)malloc(sizeof(char)*(len+1));
memset(str,0,sizeof(char)*(len+1));
int size = 0;
while((*s)!='\0')
{
char tmp = *s;
if(tmp>='A'&&tmp<='Z')
{
tmp+=32;
str[size++] = tmp;
}
else if(tmp>='a' && tmp<='z')
{
str[size++] = tmp;
}
else if(tmp>='0'&&tmp<='9')
{
str[size++] = tmp;
}
s++;
}
bool is_rsa = is_rsame(str,0,size-1);
free(str);
return is_rsa;
}
六.最多删除一个字符得到回文
题目分析

- 总结
数据格式——小写字母
要求——不删是回文或者删除一个是回文
返回——布尔值
思路分析
不删除我们很显然知道,删除一个是回文怎么删呢?如果左移删一个,不是回文,但是右移删一个,是回文,这可怎么办呢?答案——都走一遍不就知道了,只要有一边是回文的不就行了?这就是小孩子才做选择,我全都要!
- 总结
遇到不相等时,就左边走一次,右边再走一次,两个有一个为真,就返回真,否则就返回假。
代码
bool judge(char* s,int left,int right)
{
while(left<=right)
{
if(s[left]!=s[right])
{
return false;
}
left++;
right--;
}
return true;
}
bool is_rsame(char* s, int left, int right)
{
int count = 0;
while(left<=right)
{
if(s[left]!=s[right])
{
//有一边是回文就返回真
if(judge(s,left,right-1)||judge(s,left+1,right))
{
return true;
}
else
{
return false;
}
}
left++;
right--;
}
return true;
}
bool validPalindrome(char * s)
{
int len = strlen(s);
bool is_true = is_rsame(s,0,len-1);
if(is_true)
{
return true;
}
return false;
}
七.回文子字符串的个数
题目分析
- 总结
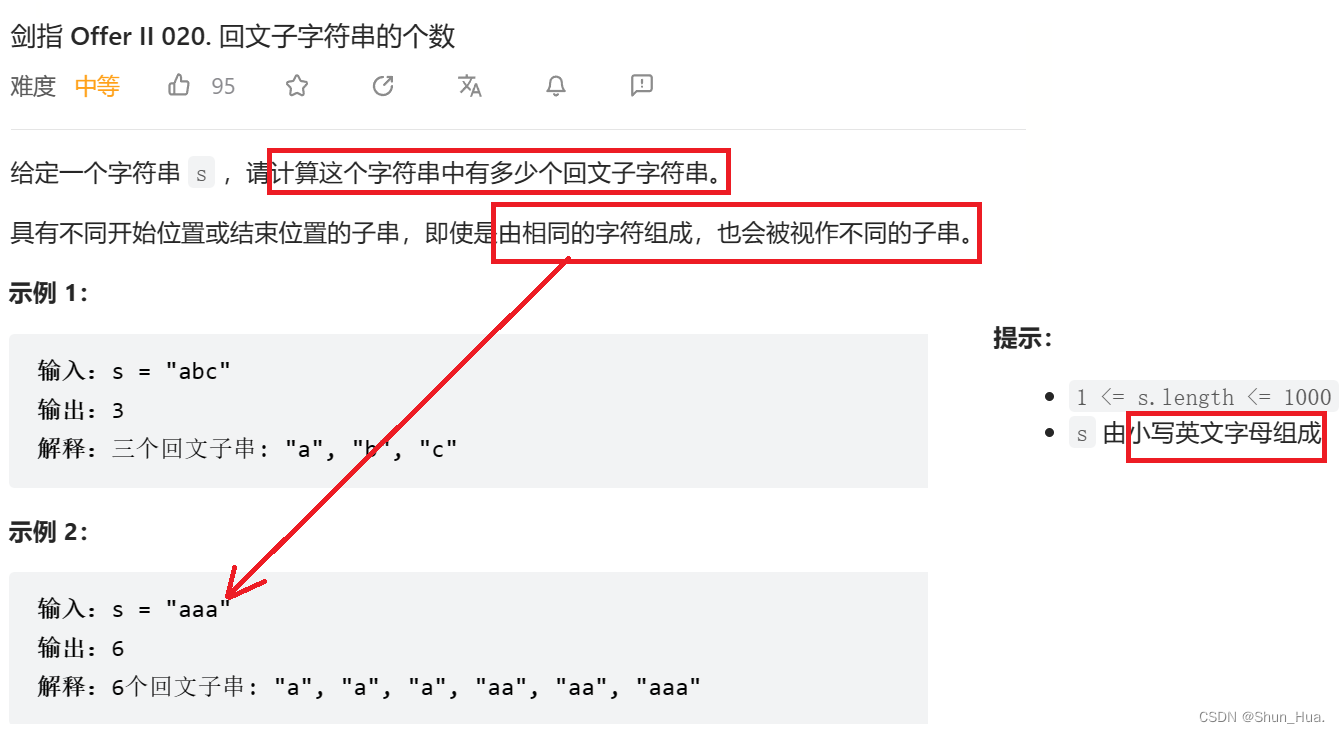
1.数据格式——小写英文字母
2.要求——求字符串有多少个回文字符串
3.返回值——回文字符串的个数
思路分析
Manacher 算法,俗称"马拉车算法",适合这类题。
这里就不多赘述了,得扯好大一会儿,详见——
1.最长回文子串问题
2.用心制作,来理解Manacher算法吧(力扣,最长回文子串)
代码——马拉车算法
int countSubstrings(char * s)
{
//第一步:处理字符串
//为了防止越界的问题发生,我们在开头和结尾放上两个不同的特殊字符,还要为\0留位置
//两个特殊的字符我们用$和!
//中间的字符串的分割符用#
//字符串的长度为n因此需要有n+1个间隔
//总计:需要开辟n + n+1 + 2 +1总共2*n+4个空间
int len = strlen(s);
char *str = (char*)malloc(sizeof(char)*(2*len + 4));
memset(str,0,sizeof(char)*(2*len+4));
//开头和结尾放上特殊字符
str[0] = '$';
str[2*len+2] = '!';
for(int i = 0; i < len; i++)
{
str[2*i + 1] = '#';
str[2*i + 2] = s[i];
}
str[2*len+1] = '#';
//处理好字符串后,我们要开辟一个空间存储,中心下标最长回文子串中子串的个数
//除去\0总共有2*len + 3个,因此要开这么大个数组
int *nums = (int*)malloc(sizeof(int)*(2*len+3));
memset(nums,0,sizeof(int)*(2*len+3));
//马拉车算法思路
//nums[i]是用于记录回文子串的个数
//i可以说就是中心下标
int r = 1;//回文半径
for(int i = 1; i < 2*len+2;)
{
//开始进行两边拓展
//根据中心下标可以得出对称位置的下标
int left = i - r + 1;
int right = i + r - 1;
int count = r-1;
while(str[left]==str[right])
{
left--;
right++;
count++;
}
left++;
right--;
//记录当前中心下标的半径
nums[i] = count;
//到这里right如果等于i或者i+1,就一个
if(i==right||i==right-1)
{
r = 1;
i++;
continue;
}
if(i < right)
{
//当前初始位置为中心元素的下一个位置
int k = i + 1;
int flag = 0;
while(k < right)
{
//求左边的对称点
int n = 2*i - k;
int n_left = n-nums[n]+1;
if(n_left<=left)
{
//更新半径
r = 1;
i = k;
break;
}
else
{
nums[k] = nums[n];
}
k++;
}
}
}
//计算求和
int sum = 0;
for(int i = 0; i < 2*len+3; i++)
{
sum+=(nums[i]/2);
}
return sum;
}
希望有所帮助!





![[网鼎杯 2018]Fakebook1](https://img-blog.csdnimg.cn/img_convert/82ae0efe46684611be77859d4830b5e1.png)