代码随想录刷题Day55 | 392. 判断子序列 | 115. 不同的子序列

392. 判断子序列

题目：

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true

思路：

这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

所以掌握本题也是对后面要讲解的编辑距离的题目打下基础。

动态规划五部曲分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。

有同学问了，为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？

用i来表示也可以！

但我统一以下标i-1为结尾的字符串来计算，这样在下面的递归公式中会容易理解一些，如果还有疑惑，可以继续往下看。

2. 确定递推公式

在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

• if (s[i - 1] == t[j - 1])
  • t中找到了一个字符在s中也出现了
• if (s[i - 1] != t[j - 1])
  • 相当于t要删除元素，继续匹配

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1（如果不理解，在回看一下dp[i][j]的定义）

if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

3. dp数组如何初始化

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：

如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。

dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。

其实这里只初始化dp[i][0]就够了，但一起初始化也方便，所以就一起操作了，代码如下：

vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));

4. 确定遍历顺序

同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

如图所示：

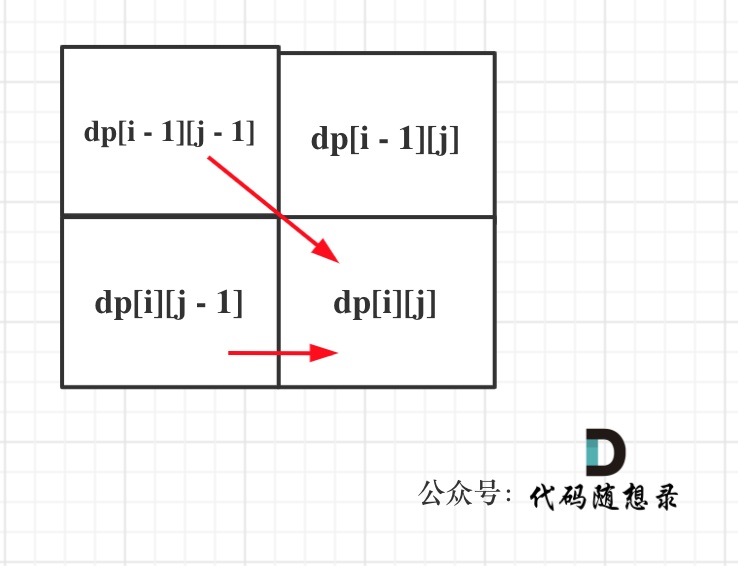
5. 举例推导dp数组

以示例一为例，输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下：

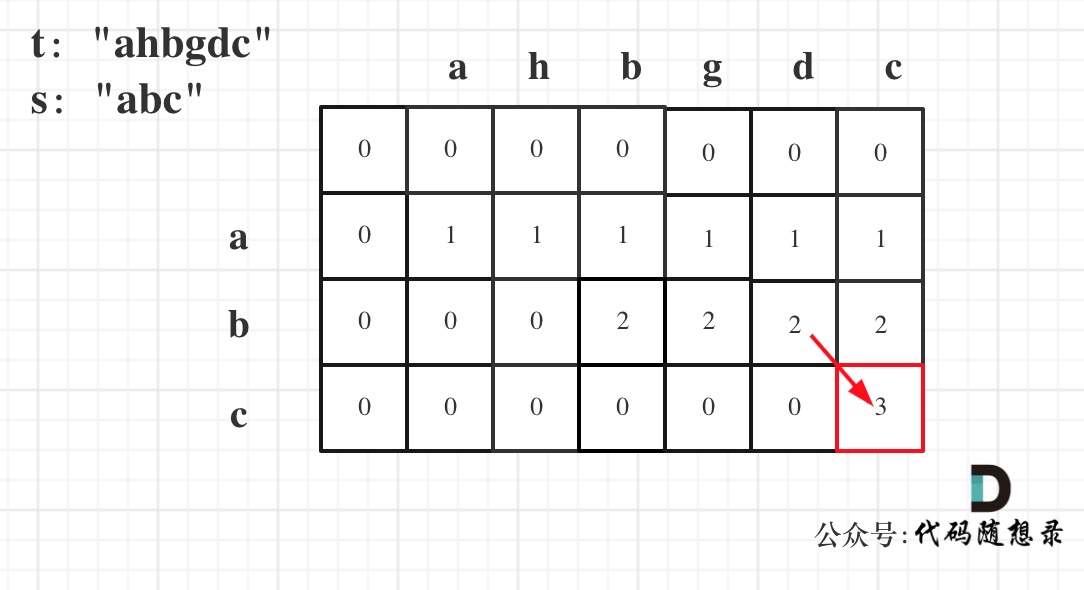
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。

图中dp[s.size()][t.size()] = 3， 而s.size() 也为3。所以s是t 的子序列，返回true。

代码：

class Solution {
    public boolean isSubsequence(String s, String t) {
        //动态规划
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for(int i = 1; i <= s.length(); i++){
            for(int j = 1; j <= t.length(); j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[s.length()][t.length()] == s.length();
    }
}

115. 不同的子序列

题目：

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

思路：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

2. 确定递推公式

这一类问题，基本是要分析两种情况

• s[i - 1] 与 t[j - 1]相等
• s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。

一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

这里可能有同学不明白了，为什么还要考虑 不用s[i - 1]来匹配，都相同了指定要匹配啊。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配，即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

3. dp数组如何初始化

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][0] 和dp[0][j]是一定要初始化的。

每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

初始化分析完毕，代码如下：

vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起，但我为了凸显初始化的逻辑，所以还是加上了。

4. 确定遍历顺序

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。

代码如下：

for (int i = 1; i <= s.size(); i++) {
    for (int j = 1; j <= t.size(); j++) {
        if (s[i - 1] == t[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        } else {
            dp[i][j] = dp[i - 1][j];
        }
    }
}

5. 举例推导dp数组

以s：“baegg”，t："bag"为例，推导dp数组状态如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NwNGYpFD-1670213145003)(https://dum1615.oss-cn-chengdu.aliyuncs.com/115.%E4%B8%8D%E5%90%8C%E7%9A%84%E5%AD%90%E5%BA%8F%E5%88%97.jpg)]

如果写出来的代码怎么改都通过不了，不妨把dp数组打印出来，看一看，是不是这样的。

代码：

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[t.length() + 1][s.length() + 1];
        for (int i = 0; i < s.length() + 1; i++) {
            dp[0][i] = 1;
        }
        for(int i = 1; i <= t.length(); i++){
            for(int j = 1; j <= s.length(); j++){
                if(s.charAt(j - 1) == t.charAt(i - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + dp[i][ j -1];
                }else{
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        // System.out.print(Arrays.deepToString(dp));
        return dp[t.length()][s.length()];
    }
}