概览

先上个图

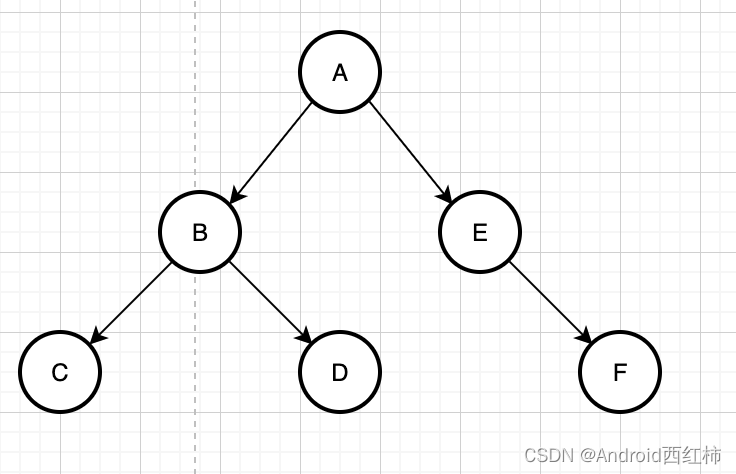
现在我们要访问图中的每个节点，即图的遍历。

图的遍历是指，从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。
我们根据访问节点的顺序与方式（根据搜索方法），可以分为广度优先（BFS）和深度优先（DFS），这是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等。

我们分别来介绍

一、深度优先（DFS）

深度优先搜索（Depth-First-Search），简称 DFS。
我们以上图为例，现在需要访问每个节点，且只访问一次，可以看到，图分成了很多之路，

主要思路是从图中一个未访问的顶点 V （比如A）开始，沿着一条路一直走到底，深入到不能再深入为止（够深），然后从这条路尽头的节点回退到上一个节点， 如果上一个节点存在没有探索的分支，便继续探索若没有则继续回退，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。

这就是暴力穷举，

1.1 图解过程

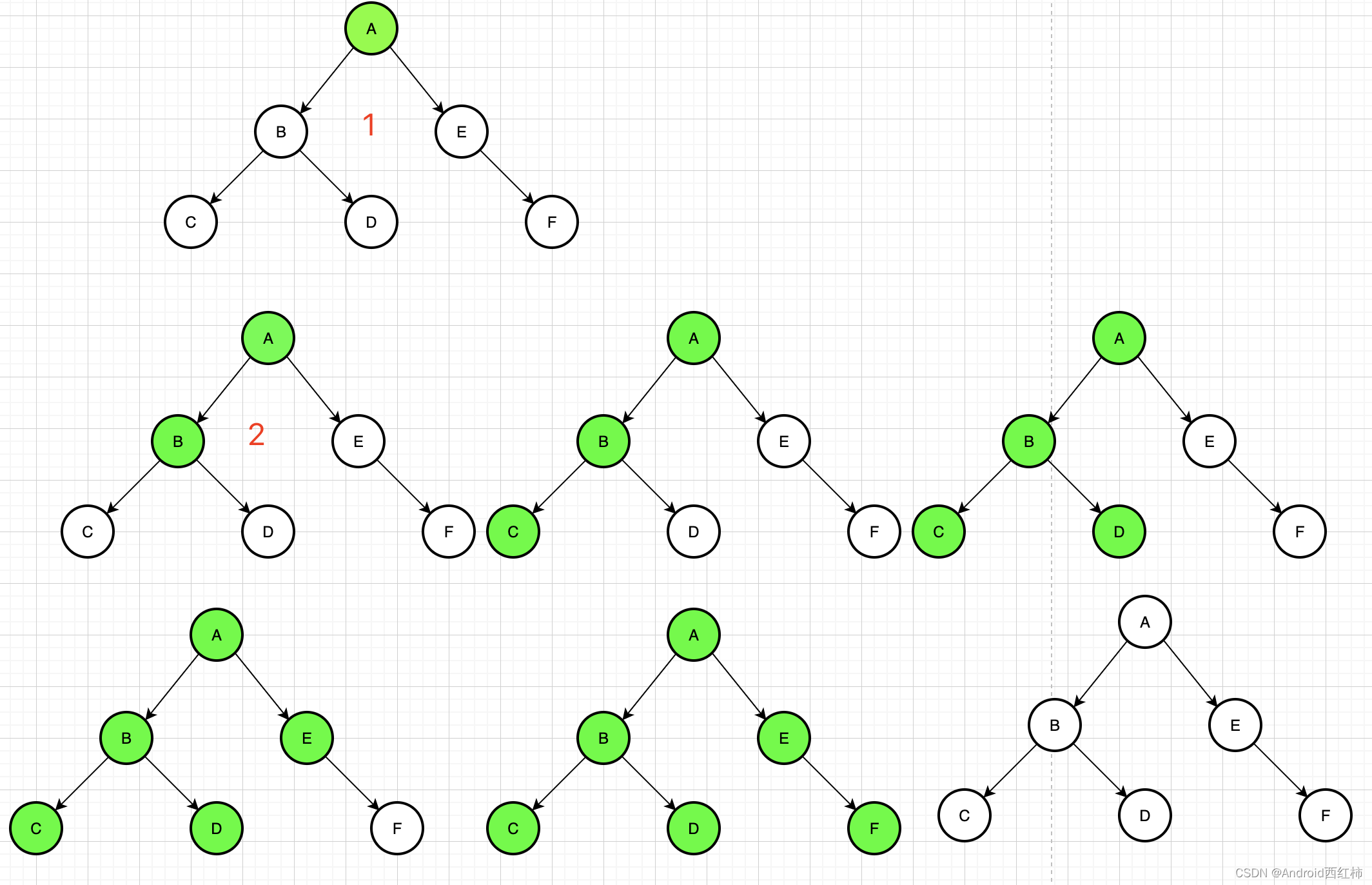
1、我们从根节点 A 开始遍历，它相邻的节点有 B，E，先遍历节点 B，再遍历 B 的子节点 C
2、上图中一条路已经走到底了(C是叶子节点，再无可遍历的节点)，此时就从 C 回退到上一个节点 B，看下节点 B 是否还有除 C 以外的节点，发现 B有 D节点，然后遍历D，
3、同理，上图中一条路已经走到底了(D是叶子节点，再无可遍历的节点)，此时就从 D 回退到上一个节点 B，B的节点都遍历过了，然后在回到A， 同样的逻辑，再到，E、F

1.2 java 实现

package com.test;

import java.util.ArrayList;
import java.util.List;

public class DepthFirstSearch {

    // 定义图结构
    private List<Integer>[] graph;

    // 构造函数，初始化图结构
    public DepthFirstSearch(int numVertices) {
        graph = new ArrayList[numVertices];
        for (int i = 0; i < numVertices; i++) {
            graph[i] = new ArrayList<>();
        }
    }

    // 添加边
    public void addEdge(int v1, int v2) {
        graph[v1].add(v2);
    }

    // 深度优先搜索算法实现
    public void dfs(int start) {
        boolean[] visited = new boolean[graph.length]; // 标记每个顶点是否被访问过
        dfsHelper(start, visited); // 递归实现深度优先搜索算法
    }

    // 递归实现深度优先搜索算法
    private void dfsHelper(int vertex, boolean[] visited) {
        visited[vertex] = true; // 标记当前顶点已被访问过
        System.out.print(geta(vertex)); // 输出当前顶点编号
        for (int neighbor : graph[vertex]) { // 遍历当前顶点的邻居顶点
            if (!visited[neighbor]) { // 如果邻居顶点未被访问过，则递归访问它
                dfsHelper(neighbor, visited);
            }
        }
    }

    private String geta(int index){
        switch (index) {
            case 0:
                return "A";
            case 1:
                return "B";
            case 2:
                return "C";
            case 3:
                return "D";
            case 4:
                return "E";
            case 5:
                return "F";
        }
        return "";
    }

    // 测试代码
    public static void main(String[] args) {
        DepthFirstSearch graph = new DepthFirstSearch(6); // 创建图结构，包含6个顶点
        graph.addEdge(0, 1); // 添加边，
        graph.addEdge(0, 4); // 添加边，
        graph.addEdge(1, 2); // 添加边，
        graph.addEdge(1, 3); // 添加边，
        graph.addEdge(4, 5); // 添加边，
        System.out.print("深度优先搜索结果："); // 输出深度优先搜索结果
        graph.dfs(0); // 从顶点0开始进行深度优先搜索
    }
}

在这个示例代码中，我们首先定义了一个DepthFirstSearch类，用于表示图结构。在构造函数中，我们初始化了图结构，并定义了一个addEdge方法，用于添加边。
然后，我们定义了一个dfs方法，用于执行深度优先搜索算法。在dfs方法中，我们首先创建了一个visited数组，用于标记每个顶点是否被访问过。然后，我们调用dfsHelper方法递归实现深度优先搜索算法。
在dfsHelper方法中，我们首先标记当前顶点已被访问过，并输出当前顶点编号。然后，我们遍历当前顶点的邻居顶点，如果邻居顶点未被访问过，则递归访问它。
最后，我们在测试代码中创建了一个包含6个顶点的图结构，并从顶点0开始进行深度优先搜索。运行测试代码后，输出深度优先搜索结果为：ABCDEF。

深度优先搜索结果：ABCDEF

二、广度优先（BFS）

广度优先遍历是首先把起点相邻的几个点探索完成，然后去探索距离起点稍远一些（隔一层）的点，然后再去玩探索距离起点更远一些（隔两层）的点… 是一层一层的向外探索。

遍历规则：
1）先访问完当前顶点的所有邻接点。(应该看得出广度的意思)
2）先访问顶点的邻接点先于后访问顶点的邻接点被访问。

2.1 图解过程

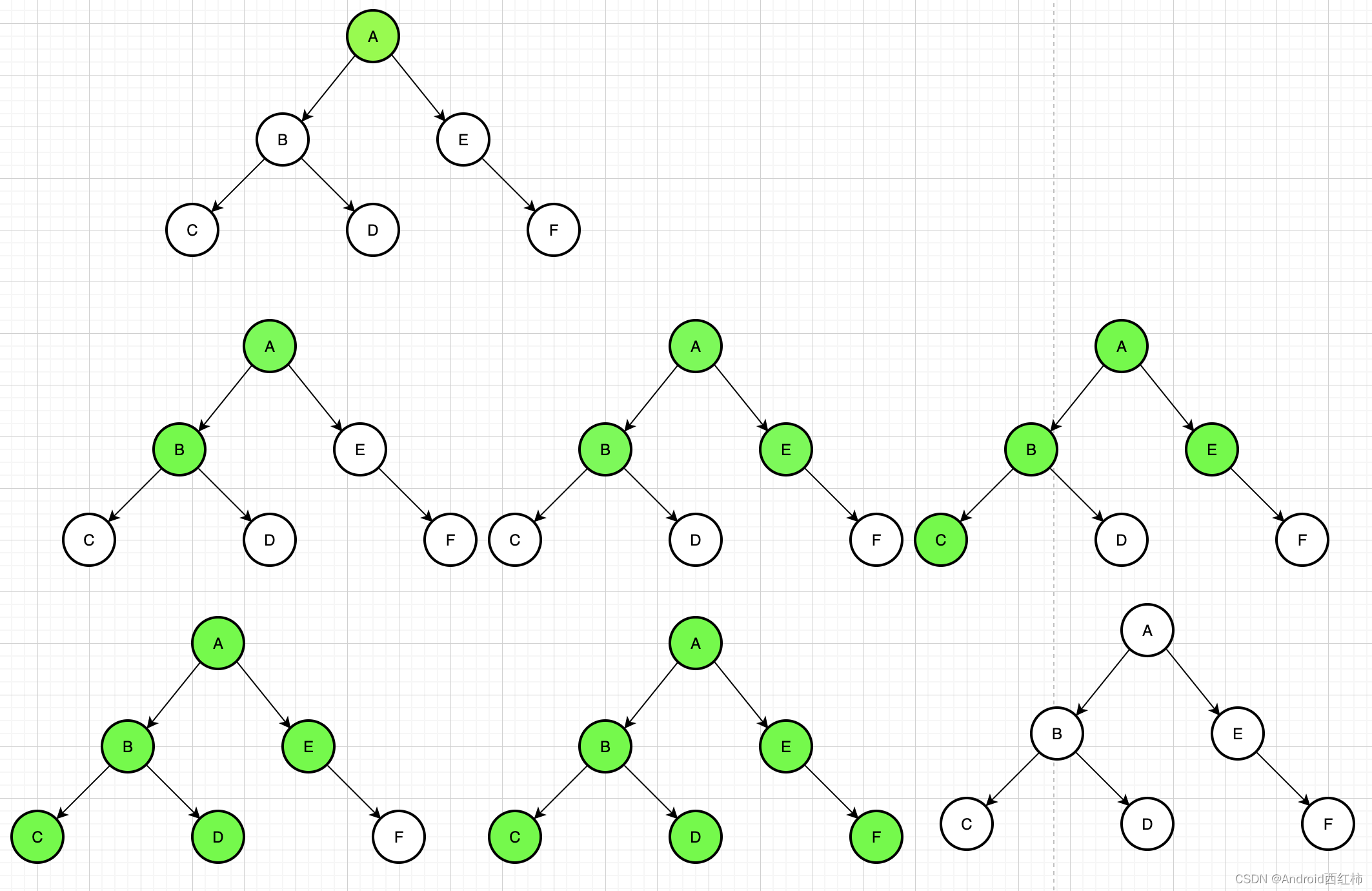
2.2 java代码实现

import java.util.*;  
  
public class BFS {  
    // 定义图结构  
    private List<List<Integer>> graph;  
  
    // 构造函数，初始化图结构  
    public BFS(int numVertices) {  
        graph = new ArrayList<>();  
        for (int i = 0; i < numVertices; i++) {  
            graph.add(new ArrayList<>());  
        }  
    }  
  
    // 添加边  
    public void addEdge(int v1, int v2) {  
        graph.get(v1).add(v2);  
        graph.get(v2).add(v1);  
    }  
  
    // 广度优先搜索算法实现  
    public void bfs(int start) {  
        boolean[] visited = new boolean[graph.size()]; // 标记每个顶点是否被访问过  
        Queue<Integer> queue = new LinkedList<>(); // 创建队列，用于存储待访问的顶点  
        visited[start] = true; // 标记起始顶点已访问过  
        queue.offer(start); // 将起始顶点加入队列中  
        while (!queue.isEmpty()) { // 当队列非空时，继续遍历队列中的顶点  
            int vertex = queue.poll(); // 取出队列头部顶点  
            System.out.print(vertex + " "); // 输出当前顶点编号  
            for (int neighbor : graph.get(vertex)) { // 遍历当前顶点的邻居顶点  
                if (!visited[neighbor]) { // 如果邻居顶点未被访问过，则标记为已访问过，并加入队列中  
                    visited[neighbor] = true;  
                    queue.offer(neighbor);  
                }  
            }  
        }  
    }  
  
    // 测试代码  
    public static void main(String[] args) {  
        BFS graph = new BFS(6); // 创建图结构，包含6个顶点  
        graph.addEdge(0, 1); // 
        graph.addEdge(0, 4); // 
        graph.addEdge(1, 2); //   
        graph.addEdge(1, 3); // 
        graph.addEdge(4, 5); // 
        System.out.print("广度优先搜索结果："); // 输出广度优先搜索结果  
        graph.bfs(0); // 从顶点0开始进行广度优先搜索  
    }  
}

在这个示例代码中，我们首先定义了一个BFS类，用于表示图结构。在构造函数中，我们初始化了图结构，并定义了一个addEdge方法，用于添加边。
然后，我们定义了一个bfs方法，用于执行广度优先搜索算法。在bfs方法中，我们首先创建了一个visited数组，用于标记每个顶点是否被访问过。
然后，我们创建了一个队列，用于存储待访问的顶点。我们将起始顶点加入队列中，并标记为已访问过。然后，我们开始遍历队列中的顶点。对于每个队列头部顶点，我们输出其编号，并遍历其邻居顶点。如果邻居顶点未被访问过，则将其标记为已访问过，并加入队列中。
最后，我们使用一个测试代码来测试我们的广度优先搜索算法实现。运行测试代码后，输出广度优先搜索结果为：0 1 2 3 4 5。

三、总结

3.1 深度优先遍历：

1、对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历（我们前面使用的是先序遍历）。
2、不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。
3、一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

3.2 广度优先遍历：

1、又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止
2、保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快。
3、一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题