一.
费诺曼(Fano)编码是一种前缀编码,其基本原理是将出现频率较高的符号用短的编码表示,而出现频率较低的符号则用长的编码表示。通过这种方式进行编码,可以达到更好的压缩效果。
费诺曼编码的具体过程如下:
- 将要编码的符号按照出现频率从高到低排序;
- 将所有符号分成两组,使得每组中包含的符号的出现频率之和相近(或者完全相等);
- 对每个组进行递归子编码,为每个符号添加一个0或1表示它属于哪个组;
- 合并所有的编码,并加上每个符号所对应的标记。
二.
霍夫曼(Huffman)编码是一种经典的前缀编码技术,通常用于数据压缩领域。它的基本思想是对不同符号的出现频率进行统计,然后根据不同符号出现的概率来构造不同长度的编码,以达到信息的最优压缩。
霍夫曼编码具体的过程如下:
- 给定一个要编码的消息,统计其中每个符号的出现频率;
- 将这些符号按照出现频率从低到高排序;
- 将出现频率最小的两个符号合并成一个新的节点,该节点的权值为两个符号的权值之和;
- 在剩下的符号中重新选择出现频率最小的两个相邻节点,并合并成一个新的节点,直到所有节点都被合并成一个根节点;
- 对于左子树,或者说选择编码时向左转的子节点,标志位设为0;而对于右子树,或者说选择编码时向右转的子节点,标志位设为1;
- 根据上述规则生成每个符号的霍夫曼编码,为了避免编码冲突,保证任意一个编码序列不是另一个编码序列的前缀;
- 将原始消息通过使用霍夫曼编码表进行编码并压缩,压缩后的数据通常比原数据短,从而实现有效的数据压缩。
三.
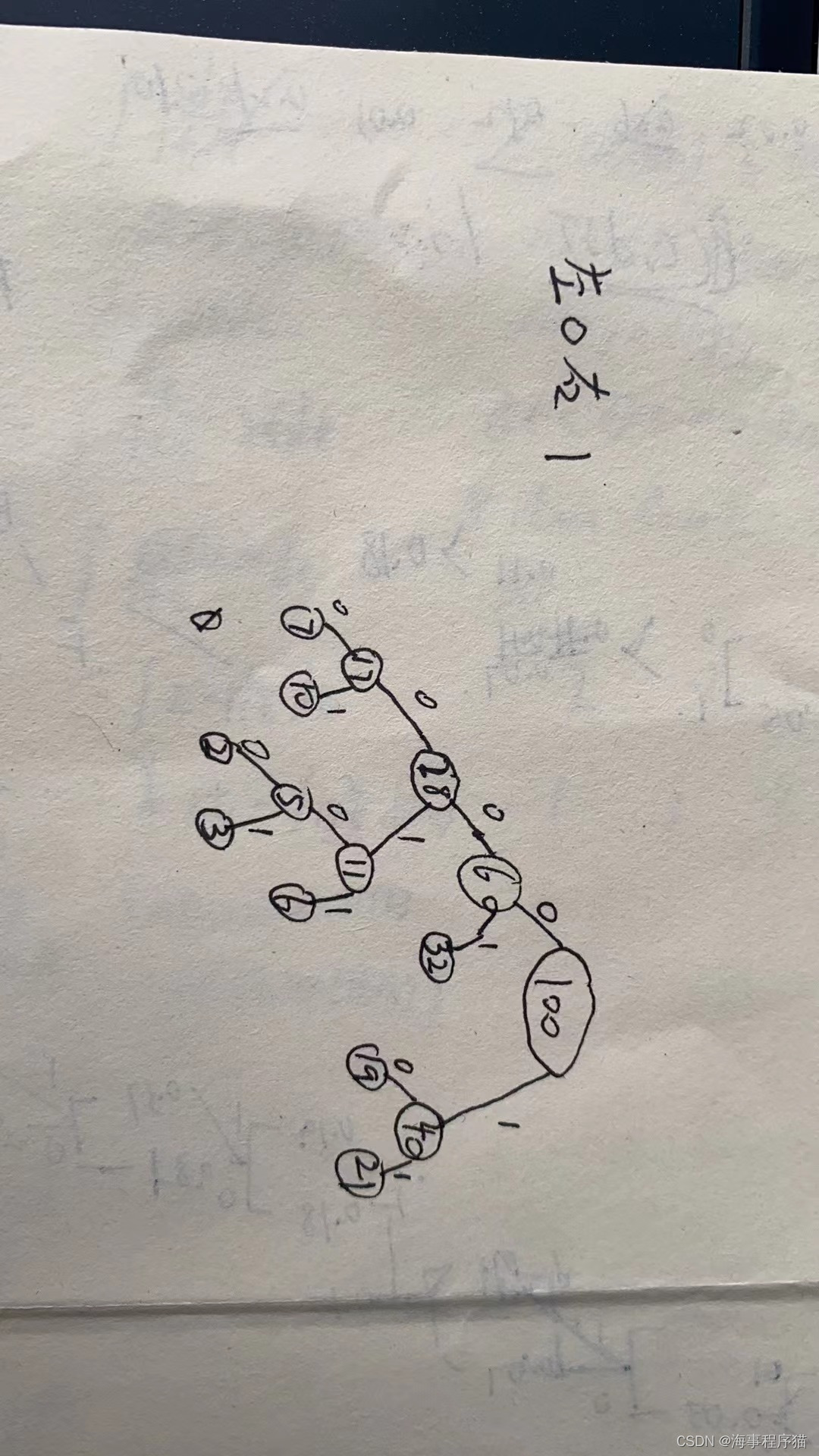
哈夫曼树是一种被压缩数据的编码方法,根据哈夫曼树的定义,当一条边向左分支走时,我们可以将其用二进制0表示;当一条边向右分支走时,我们可以将其用二进制1表示。因此,哈夫曼树的存储可以使用0表示左分支,使用1表示右分支。
哈夫曼树编码的具体过程如下:
- 统计字符集中每个字符出现的频率,并将它们作为叶子节点加入到一个森林中;
- 选取两个频率最小的节点合并成一个新的节点,该新节点的权值为两个节点的权值之和。此时这两个节点在森林中被移除,同时将新生成的节点插入到森林中;
- 重复第二步操作,直到森林中只剩下一个节点,即为哈夫曼树的根节点;
- 对于哈夫曼树中的每个叶子节点,定义其编码为从根节点到该叶子节点所经过的路径上所有左转弯所组成的二进制数字(或者所有右转弯组成的数字)。例如:从根节点到叶子节点A依次经过了3个左转弯,则叶子节点A的编码为"000"。
费诺曼编码

霍夫曼编码

哈夫曼树编码