参考资料：leetCode评论区大佬, 《程序员代码面试指南》

思路1：使用单调栈

维持一个从栈底到栈顶中的元素——下标，对应到数组是从大到小排序。
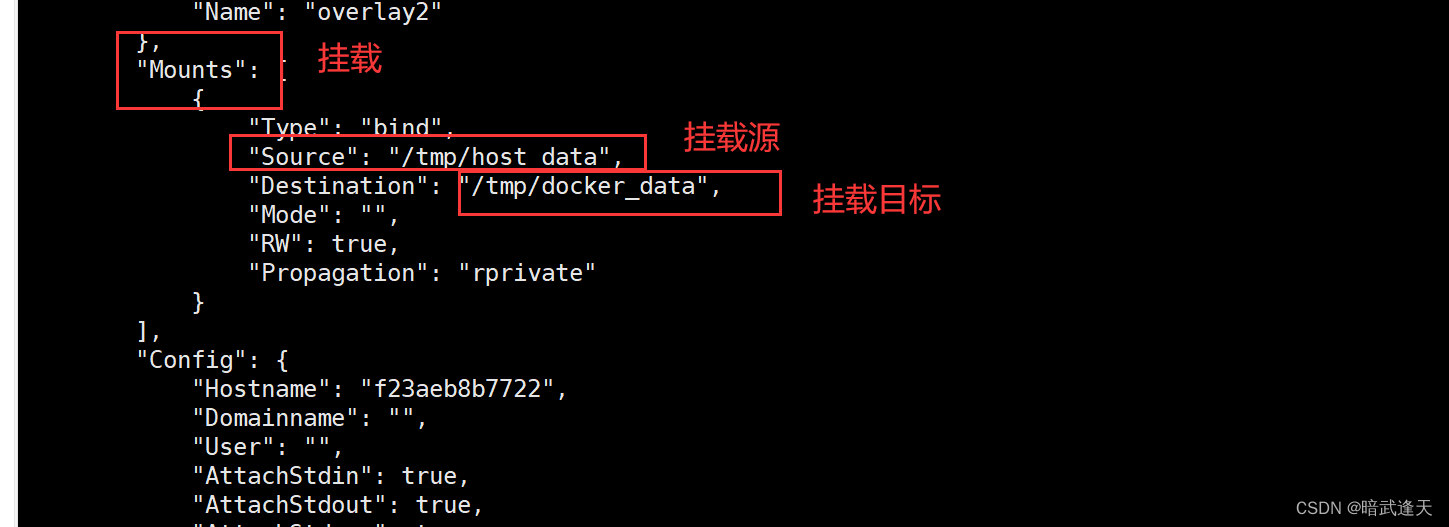
遍历数组，如果新值大于栈顶元素（下标）对应的数组值，那么弹出栈顶，并为栈顶元素计算这次弹出位置所在小范围[l,r]的存水量（注意：并不是这个弹出位置（总共）能够存的水量，以下图中index=5处为例，弹出位置5 所在小范围的存水量是1，但位置5总共能够存的水量是2）

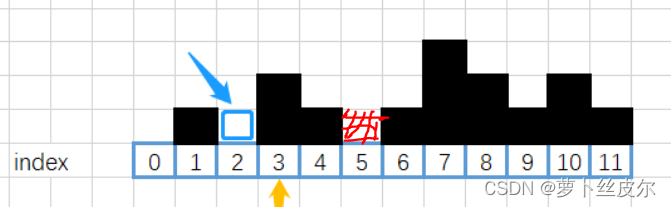
当弹出位置为4时，我们计算的 其所在小范围的存水量是 3，即下面标黄的部分。

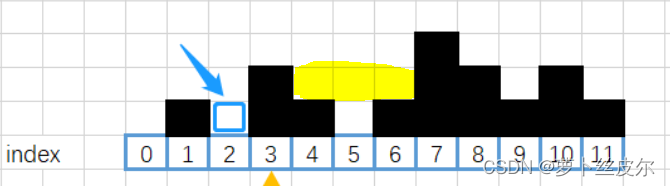
（假设位置cur被弹出，它原来在栈中压的位置是l (也就是在自己左边、离自己最近、比自己大的)，促使它弹出的位置是r(也就是在自己左边、离自己最近、比自己大的)）
$$(Min(nums[l],nums[r])-nums[cur])\times (r-l-1)$$

 public int trap(int[] height) {
        int n = height.length;
        Stack<Integer> stack = new Stack<>();
        int sum=0;
        for(int i=0;i<n;i++){

            while(!stack.isEmpty() && height[stack.peek()]<=height[i]){
                int cur = stack.pop();
                if( !stack.isEmpty())
                {
                    sum += Math.max(height[i],height[stack.peek()])-height[cur];
                }
            }

思路2：使用辅助空间记录前缀最大值，后缀最大值

对于位置i来说，找其左侧的最大值l，其右侧的最大值r, 所以，位置i所能存的总水量就是 $Max(0,Min(l,r)-nums[i])$ 。注：最外层取max是防止出现 负的水量。
具体地，使用一个变量不断更新后缀最大值，这样避免申请新的辅助空间。

 public int trap(int[] height) {
          // help[i] = [...i].max , 这个最高值可能并不是 离自己最近的 ， 所以我们计算的是位置i总共能够存多少水， 注意是“总共”，而不是“所在小范围”
          int n = height.length;
          int[] help = new int[n];
          help[0]=height[0];
          for(int i=1;i<n;i++){
              help[i] = help[i-1]>height[i]?help[i-1]:height[i];
          }
            int max=height[n-1],idx=n-1;
            int sum=0;
          for(int i=n-2;i>=1;i--){
              sum += Math.max(0,Math.min(help[i-1],max)-height[i]);
              max = Math.max(max,height[i]);
          }
        return sum;
      }

思路3：双指针

思路：
左指针l从1位置开始，右指针r从n-2位置开始，
maxL = nums[…l-1].max;
maxR = nums[r+1…].max;
每次比较maxL和 maxR，选小的，比如maxL, 那么结算位置l它自己的总水量，即
$Max(maxL-nums[l],0)$，加入到sum中；然后更新maxL, l++.
原理是：接上，对于nums[l]来说，它的存水高度的短板已经出现了，也就是maxL.那么位置l的存水量也就可以确定了。

public int trap(int[] height) {
          if(height==null||height.length<3){return 0;}
          int maxL=height[0],maxR=height[height.length-1]; // 
          int l=1, r=height.length-2;
          int sum=0;
          while(l<=r){
              if(maxL<=maxR){

                  sum+=Math.max(maxL-height[l],0);
                  maxL = Math.max(maxL,height[l]);
                  l++;
                
              }else{
                  sum+=Math.max(maxR-height[r],0);
                  maxR=Math.max(maxR,height[r]);
                  r--;
              }

          }

        return sum;
      }