决策树知识点
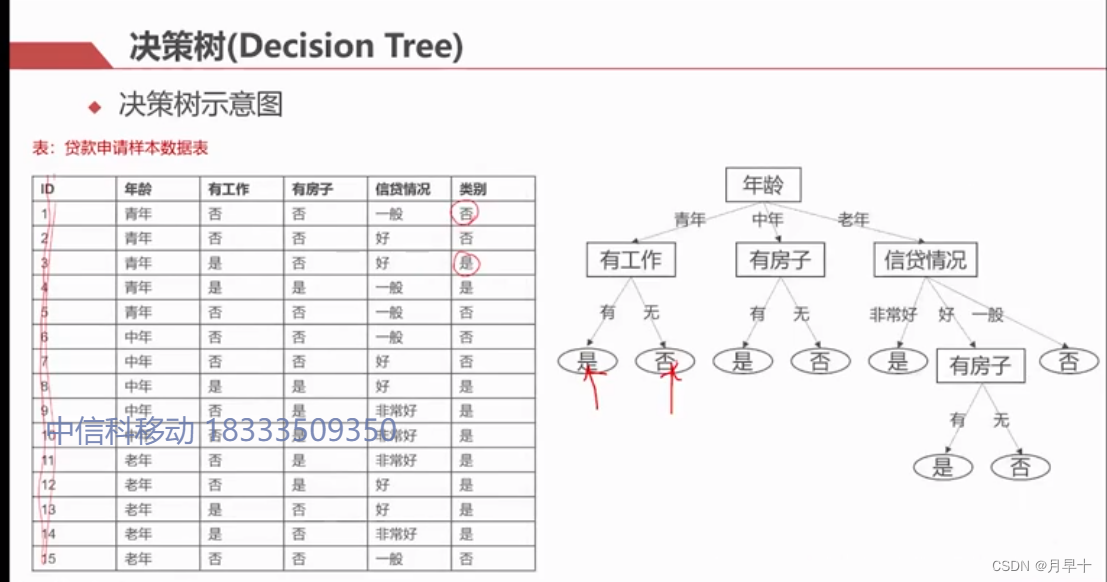
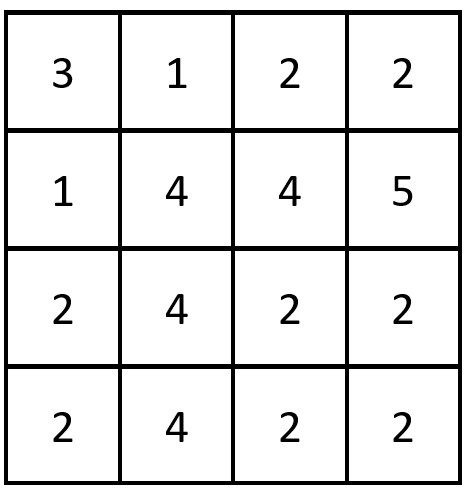
- 这个表也是一个数据集
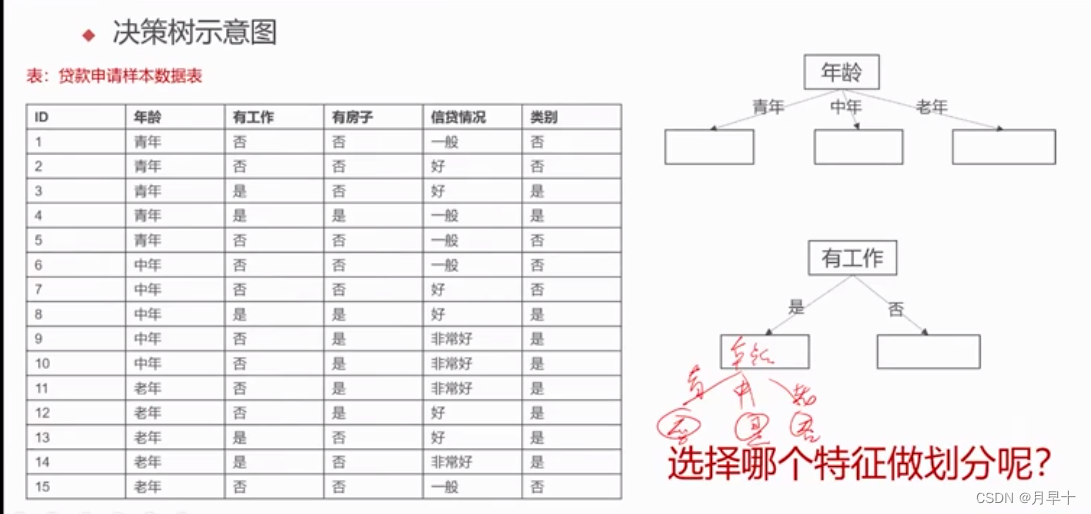
- 问题:以什么作为划分呢?第一次是以年龄,还是以 工作 房子 信贷情况…
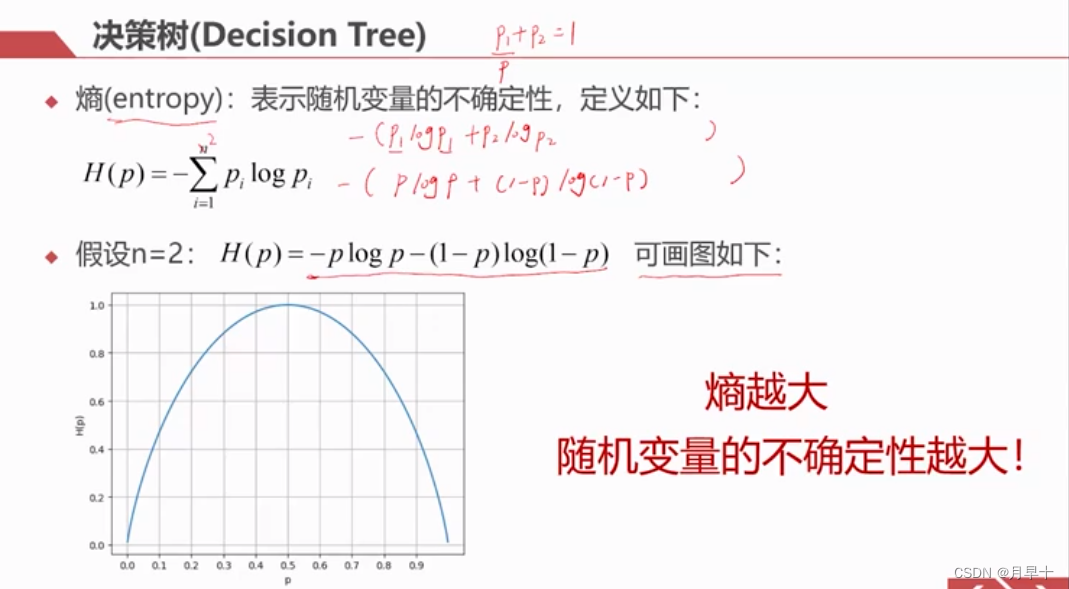
- 这里的熵与中文里的其他东西没有实际对应,就是一个定义
- H(p)=1最大时,p=0.5,这表示既可能p1也可能是p2,两种可能性一样,或者说不确定性最大。
- 当H(p)减小时,p的值改变了,更加趋向于一个确定的可能
- 一般我们希望,熵越来越小,以得到一个确定的结果。
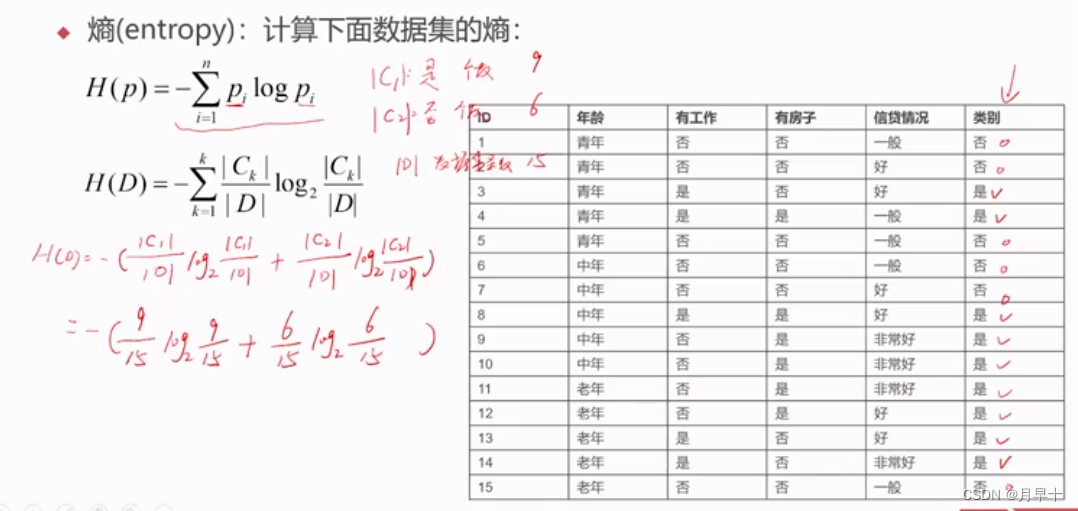
- C1是选项C1的个数 ,C2是选项C2的个数…,D是所有选项的总数
- 在这里,以类别为例子,C1=类别为是的个数=9 ,C2=类别为否的个数=6 ,只有这两种C, D=总数=15
- 于是计算出数据集的熵 H(D)

- 我们想要的是条件熵,在给定数据集某一个条件X下的熵。
- 比如以 年龄/工作/房子/信贷情况 为条件,算出来的条件熵。这个条件熵越大,表示在这个条件下这个数据集越不确定。 然后就可以以这个最不确定的条件作为第一个划分。

-
信息增益是知道了某个条件后,事件的不确定性下降的程度

-
图中的H(D1)就是给定A1为条件时的条件熵,即H(D|A1)
-
图中A3(房子)是最大的,可以说A3是不确定性最高,最适合做第一个划分点的

-
划分完后,将划分过来的数据集进行第二次划分,对划分过来的数据集再次进行计算,得到其中条件熵最大的特征,作为第二次的划分点
-
如此递归进行,直到所有数据都分到了叶子节点,或者定义一个深度进行到该深度后停止

算法解析
定义数据集
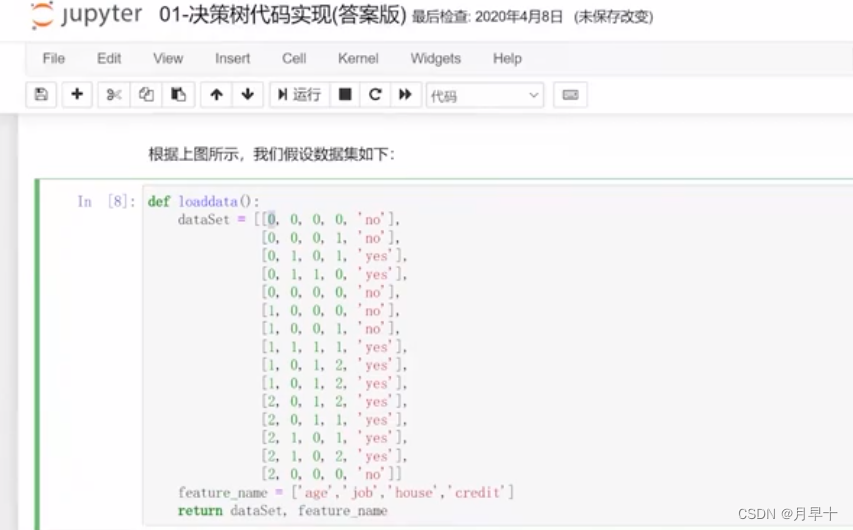

计算数据集的熵


数据集划分


- 输入数据集 要划分的类型 划分的参数
选择最优特征值

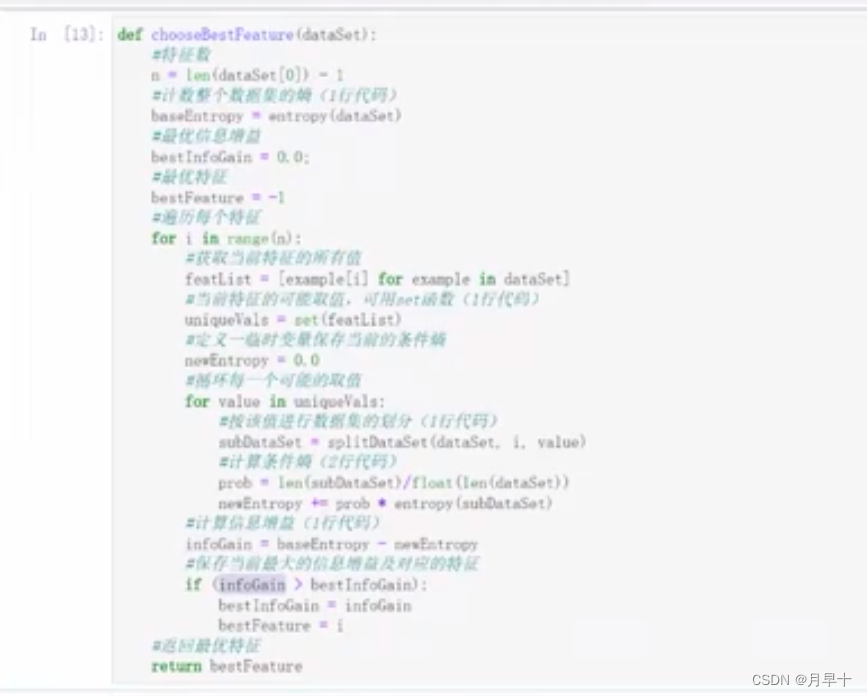
类别投票表决
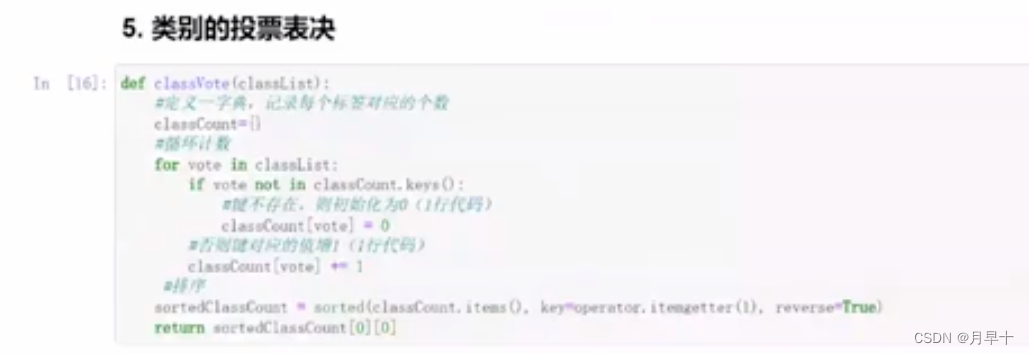
训练一颗递归树