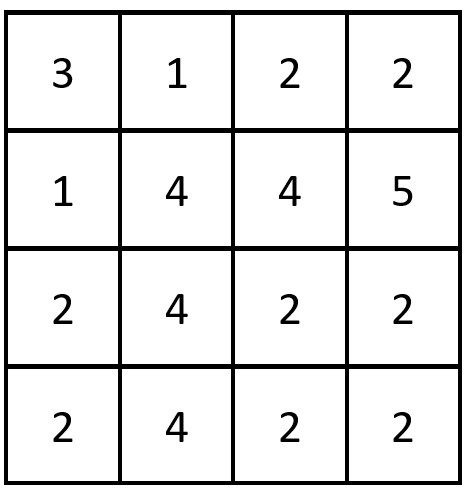
题目链接：https://leetcode.cn/problems/tiling-a-rectangle-with-the-fewest-squares/

1. 题解（1240. 铺瓷砖）

1.1 暴力深搜 – DFS

NP-Complete 问题

• 题解参考：Java DFS暴力递归（详细注释）

…
题解思路：

1. 检查当前答案是否大于等于当前最佳答案，若是，则进行剪枝，回溯
2. 检查正方形中是否有空位，若无空位，更新答案并回溯;
3. 在查找到的第一个空位，进行填充，填充的规则是由大瓷砖到小瓷砖进行尝试（从小到大会导致运行时间大大增加）;
   • 若尝试失败（部分位置可能已经被其它瓷砖占据），则更换成小瓷砖继续进行尝试。
   • 若尝试成功，则首先更新状态，并进行递归，同时在回溯时需要注意恢复状态。

…
下列代码还可参考官方题解进一步简化，如：

• setStatus无需列出 x2,y2 的坐标，直接根据增量 k 进行循环遍历即可；
• checkEmpty可省略，但省略后要确保在 dfs 的过程中是从左到右，从上到下顺序移动的；

class Solution {
    private int res; // 记录答案, 会在DFS过程中被更新
    private int row, col;
    public int tilingRectangle(int n, int m) {
        boolean[][] tiled = new boolean[n][m];
        res = Math.max(n, m);  // 初始赋值为最大值：即全为1的情况
        dfs(tiled, 0);
        return res;
    }
    
    // DFS：当前地上瓷砖状态为tiled，已经铺了count个瓷砖，继续铺下去把地面铺满
    private void dfs(boolean[][] tiled, int count) {
        if (count >= res) { // 剪枝
            return;
        }
        int[] emptyPos = checkEmpty(tiled); // 地上没瓷砖的第一个位置
        if (emptyPos[0] == -1 && emptyPos[1] == -1) { // 已经铺完了所有地方，收集答案
            res = Math.min(res, count);
            return;
        } 
        // 从大到小，开始尝试铺瓷砖
        int maxLen = Math.min(tiled.length - emptyPos[0], tiled[0].length - emptyPos[1]); 
        for (int len = maxLen; len >= 1; len--) {
            // 尝试用len*len的瓷砖的左上角去对齐地上没瓷砖的这个位置
            if (setStatus(tiled, emptyPos[0], emptyPos[1], emptyPos[0] + len - 1, emptyPos[1] + len - 1, false)) {
                dfs(tiled, count + 1);
                setStatus(tiled, emptyPos[0], emptyPos[1], emptyPos[0] + len - 1, emptyPos[1] + len - 1, true);
            } 
        }
    }

    // 尝试反转 (row1, col1) 和 (row2, col2) 之间的铺瓷砖状态
    // 必须确保这个区域内初始都是hasTiled状态，否则不会反转
    private boolean setStatus(boolean[][] tiled, int row1, int col1, int row2, int col2, boolean hasTiled) {
        for (int i = row1; i <= row2; i++) {
            for (int j = col1; j <= col2; j++) {
                if (tiled[i][j] != hasTiled) {
                    return false;
                }
            }
        }
        // 为什么不能将上下两个循环合在一起？ 这是因为只要有一个瓷砖块的状态不满足就不能反转
        for (int i = row1; i <= row2; i++) {
            for (int j = col1; j <= col2; j++) {
                tiled[i][j] = !tiled[i][j];
            }
        }
        return true;
    }

    // 顺序遍历寻找第一个没铺瓷砖的位置（从上到下，从左到右）
    private int[] checkEmpty(boolean[][] tiled) {
        for (int i = 0; i < tiled.length; i++) {
            for (int j = 0; j < tiled[0].length; j++) {
                if (!tiled[i][j]) {
                    return new int[]{i, j};
                }
            }
        }
        return new int[]{-1, -1};
    }
}

2. 参考资料

[1] 铺瓷砖 – 官方题解
[2] Java DFS 暴力递归（详细注释）
[3] NP complete概念浅析