时间序列学习 经典案例（5）【stability_selection】股票数据特征分析与特征选择

news2024/11/25 16:57:09

0.环境配置

本文用到的环境是：

  • jupyter 略
  • python 3.9
  • stability_selection 略，见下文。
  • scikit-learn 1.2.2
  • seaborn 0.12.2
  • pandas 1.3.5
  • numpy 1.22.3
  • matplotlib 3.6.3
  • tushare 1.2.89
  • baostock 00.8.80
  • yfinance 0.2.18

1.stability_selection模块安装【问题已解决并pull requests，已支持最新版本】

由于目前最新版的stability_selection已经从新版本的sklearn中剔除，所以需要单独安装，但是单独安装的stability_selection模块与旧版本互相不兼容会报错，所以这个时候需要解决这个报错。

我已经对stability_selection项目fork进行修改源码修复error，并且已发送pull requests到源项目的请求。
所以，可以使用我fork的项目进行安装该模块，已经完美兼容scikit-learn 1.2.2版本。

项目链接：https://github.com/TonyEinstein/stability-selection

官方文档地址：https://thuijskens.github.io/stability-selection/docs/index.html

源项目链接：https://github.com/scikit-learn-contrib/stability-selection

欢迎大家点个star和fork喔！

1.1 pip安装【不推荐】

pip install stability_selection

1.2从源码安装【推荐】

1.2.1git方式

切换你所要安装这个库的虚拟环境，然后进行依次执行这四个命令即可。

git clone https://github.com/TonyEinstein/stability-selection.git
cd stability-selection
pip install -r requirements.txt
python setup.py install

第一个命令是下载这个git项目，下载之后是一个文件夹；
第二个命令是进入这个下载好的文件夹；
第三个命令是安装依赖文件；
第四个命令是进行源码安装。

1.2.2手动下载源码

（1）进入 https://github.com/TonyEinstein/stability-selection页面，并下载源码到本地桌面。
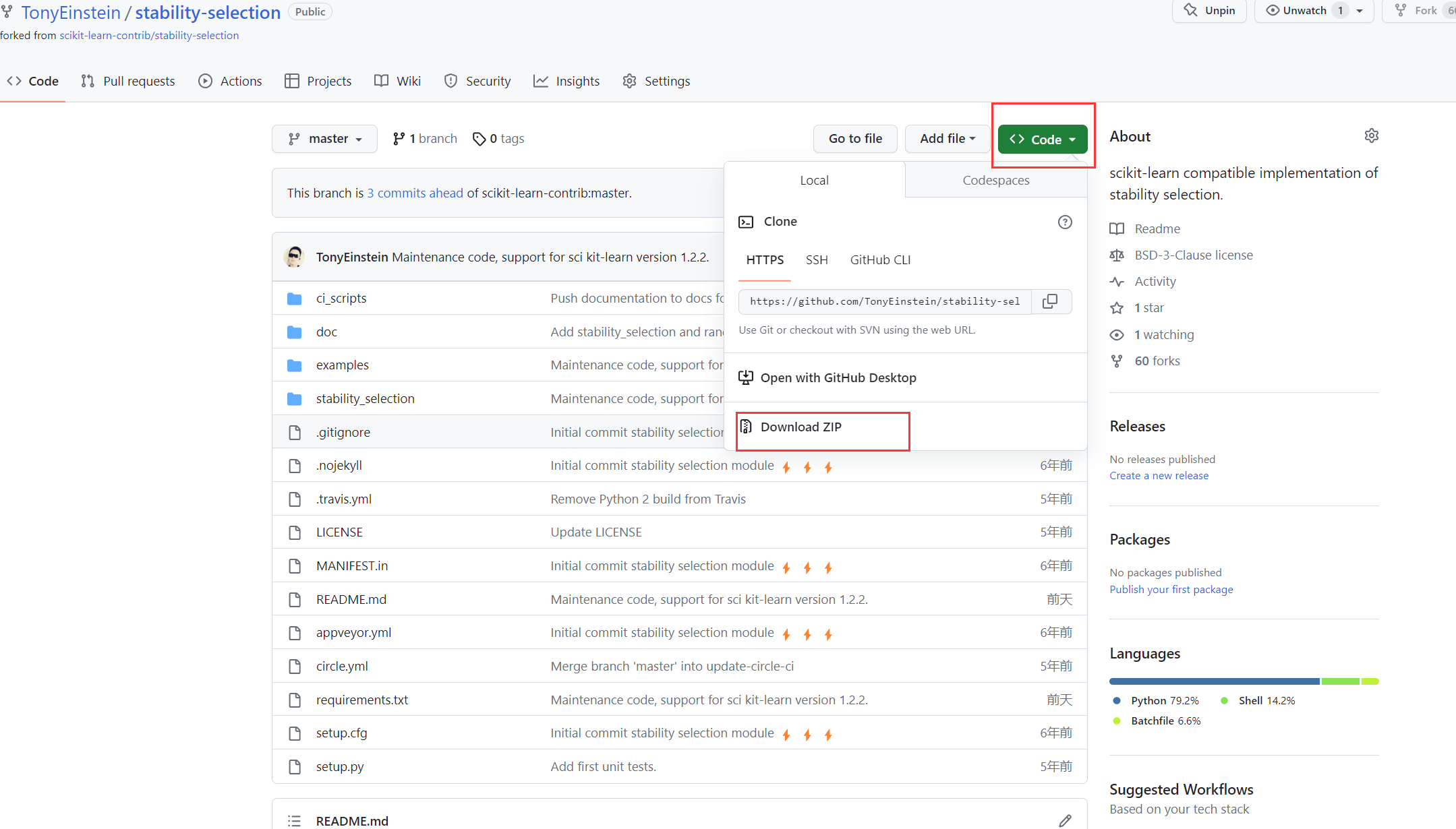
在这里插入图片描述
（2）解压该压缩包，打开命令行，并在命令行中进入到该文件夹。然后依次运行以下命令进行安装。

pip install -r requirements.txt
python setup.py install

2.数据获取

2.1Tushare模块

# 导入tushare库
import tushare as ts
# 设置token
ts.set_token('your token here')
# 初始化pro接口
pro = ts.pro_api()
# 获取日线数据
df = pro.daily(ts_code='000001.SZ', start_date='20180701', end_date='20180718')

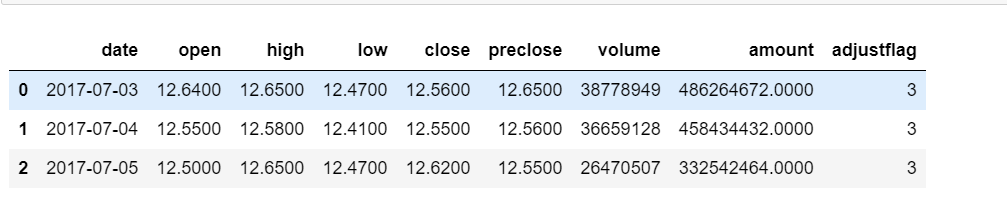
2.2 证卷宝Baostock模块

import baostock as bs
import pandas as pd

# 登陆系统
lg = bs.login()
# 获取沪深A股历史K线数据
rs_result = bs.query_history_k_data_plus("sh.600000",
                                         fields="date,open,high, low, close,preclose,volume,amount,adjustflag",
                                         start_date='2017-07-01', 
                                         end_date='2017-12-31', 
                                         frequency="d", 
                                         adjustflag="3")
df_result = rs_result.get_data()
# 登出系统
bs.logout()

df_result.head(3)

在这里插入图片描述

# 获取中国平安股票数据

import baostock as bs
# 登陆系统
lg = bs.login()
# 获取沪深A股历史K线数据
rs_result = bs.query_history_k_data_plus("sh.601318",  
                        fields="date,open,high,low,close,volume",   
                        start_date='2018-01-01',   
                        end_date='2021-03-31',  
                        frequency="d",  
                        adjustflag="3")
df_result = rs_result.get_data()
# 登出系统 
bs.logout()

df_result.head()

在这里插入图片描述

2.3Yfinance模块

import yfinance as yf
# 输入
symbol = 'AMD'
start = '2014-01-01'
end = '2018-08-27'

dataset=yf.pdr_override(symbol,start,end)
dataset.head()

获取腾讯股票数据

# 获取腾讯股票数据
"""
需要科学上网
"""
import yfinance as yf

symbol = 'TCEHY'
start = '2016-01-01'
end = '2021-03-31'
yf.pdr_override()

dataset = yf.download(symbol,start,end)


dataset.head()

在这里插入图片描述

3.常见计算

3.1滚动窗口计算


# 求最后4行的均值
dataset.rolling(window=5).mean()
dataset

在这里插入图片描述

dataset.rolling(
    window,
    min_periods=None,
    center=False,
    win_type=None,
    on=None,
    axis=0,
    closed=None,)
    
 提供滚动窗口计算。

window：也可以省略不写。表示时间窗的大小，注意有两种形式（int or offset）。如果使用int，则数值表示计算统计量的观测值的数量即向前几个数据。 如果是offset类型，表示时间窗的大小。

min_periods：每个窗口最少包含的观测值数量，小于这个值的窗口结果为NA。值可以是int，默认None。offset情况下，默认为1。

center: 把窗口的标签设置为居中。布尔型，默认False，居右

win_type: 窗口的类型。截取窗的各种函数。字符串类型，默认为None。各种类型

on: 可选参数。对于dataframe而言，指定要计算滚动窗口的列。值为列名。

axis: int、字符串，默认为0，即对列进行计算

closed：定义区间的开闭，支持int类型的window。对于offset类型默认是左开右闭的即默认为right。可以根据情况指定为left both等。

3.2指数加权函数ewm

dataset['ewm'] = dataset['Adj Close'].ewm(span=20,
                                              min_periods=0,
                                              adjust=False,
                                              ignore_na=False).mean()
dataset.head()

在这里插入图片描述

函数解析
DataFrame.ewm(com=None,  
            span=None,  
            halflife=None,  
            alpha=None,  
            min_periods=0,  
            adjust=True,  
            ignore_na=False,  
            axis=0,  
            times=None)
            
提供指数加权（EW）函数。可用EW功能：mean()，var()，std()，corr()，cov()。参数：com，span，halflife，或alpha必须提供。

4.特征构造

dataset.info()
df = dataset.copy()

df['H-L'] = df['High'] - df['Low']
df['O-C'] = df['Adj Close'] - df['Open']
df['3day MA'] = df['Adj Close'].shift(1).rolling(window=3).mean()
df['10day MA'] = df['Adj Close'].shift(1).rolling(window=10).mean()
df['30day MA'] = df['Adj Close'].shift(1).rolling(window=30).mean()
df['Std_dev'] = df['Adj Close'].rolling(5).std()
df.head()

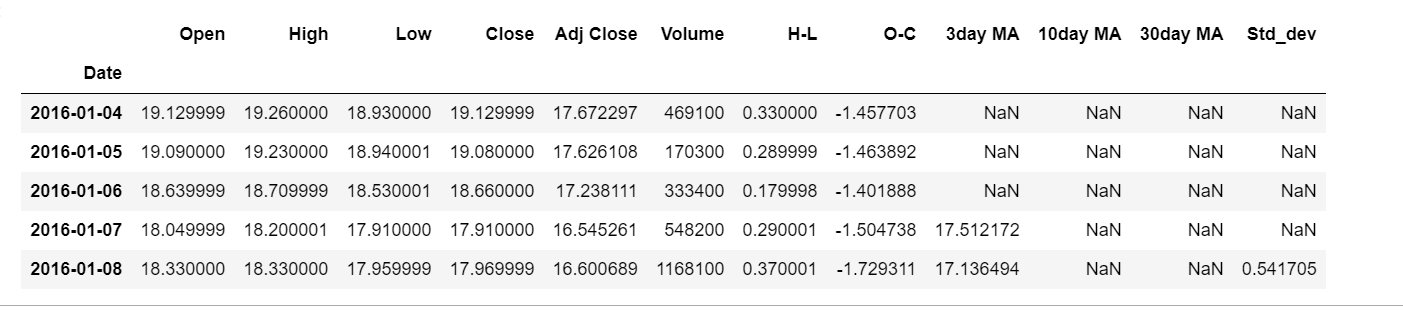
在这里插入图片描述

# 描述性统计
df.describe().T

# 检测缺失值
df.isnull().sum()

# 缺失值可视化
import matplotlib.pyplot as plt

df_missing_count = df.isnull().sum() 
# -1表示缺失数据
# 另一个不常见的设置画布的方法
plt.rcParams['figure.figsize'] = (15,8)
df_missing_count.plot.bar()
plt.show()

print("column nunique  NaN")
for column in df:
    print("{0:10} {1:6d} {2:6}".format(
          column, df[column].nunique(), 
          (df[column] == -1).sum()))

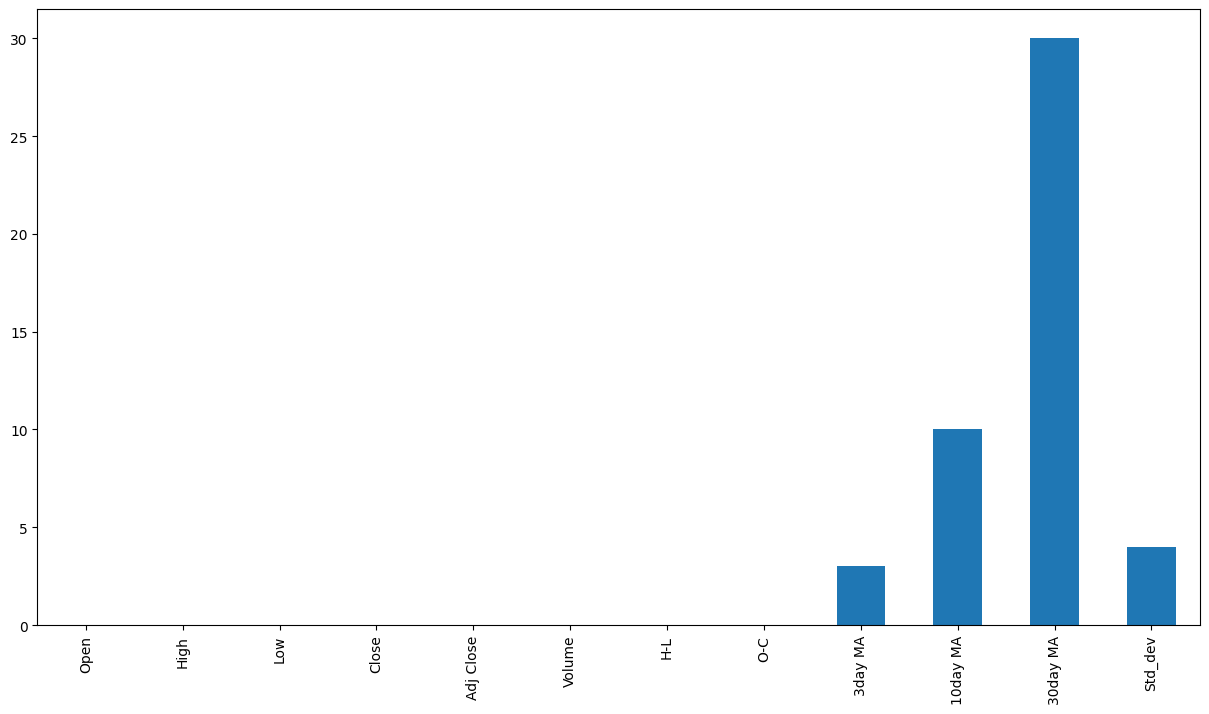
在这里插入图片描述

column nunique  NaN
Open         1136      0
High         1141      0
Low          1082      0
Close        1156      0
Adj Close    1231      0
Volume       1308      0
H-L           390      0
O-C          1317      0
3day MA      1302      0
10day MA     1306      0
30day MA     1288      0
Std_dev      1311      0

5.特征间相关性分析

import seaborn as sns
# 一个设置色板的方法
# cmap = sns.diverging_palette(220, 10,as_cmap=True)
sns.heatmap(df.iloc[:df.shape[0]].corr()
        ,annot = True, cmap = 'Blues')

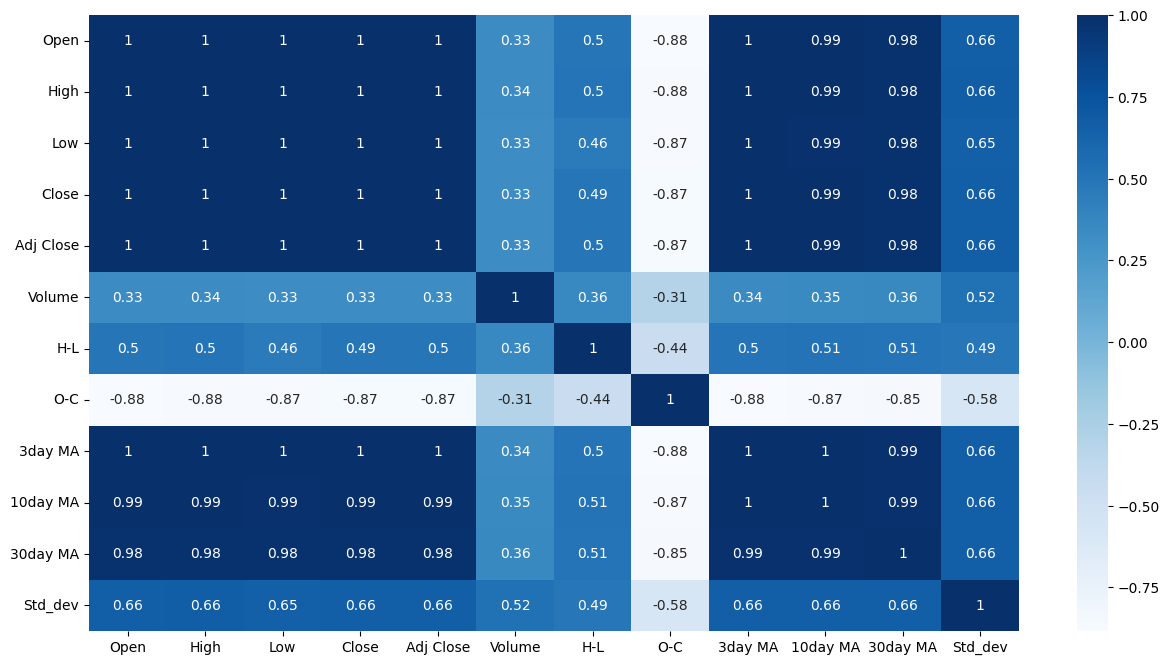
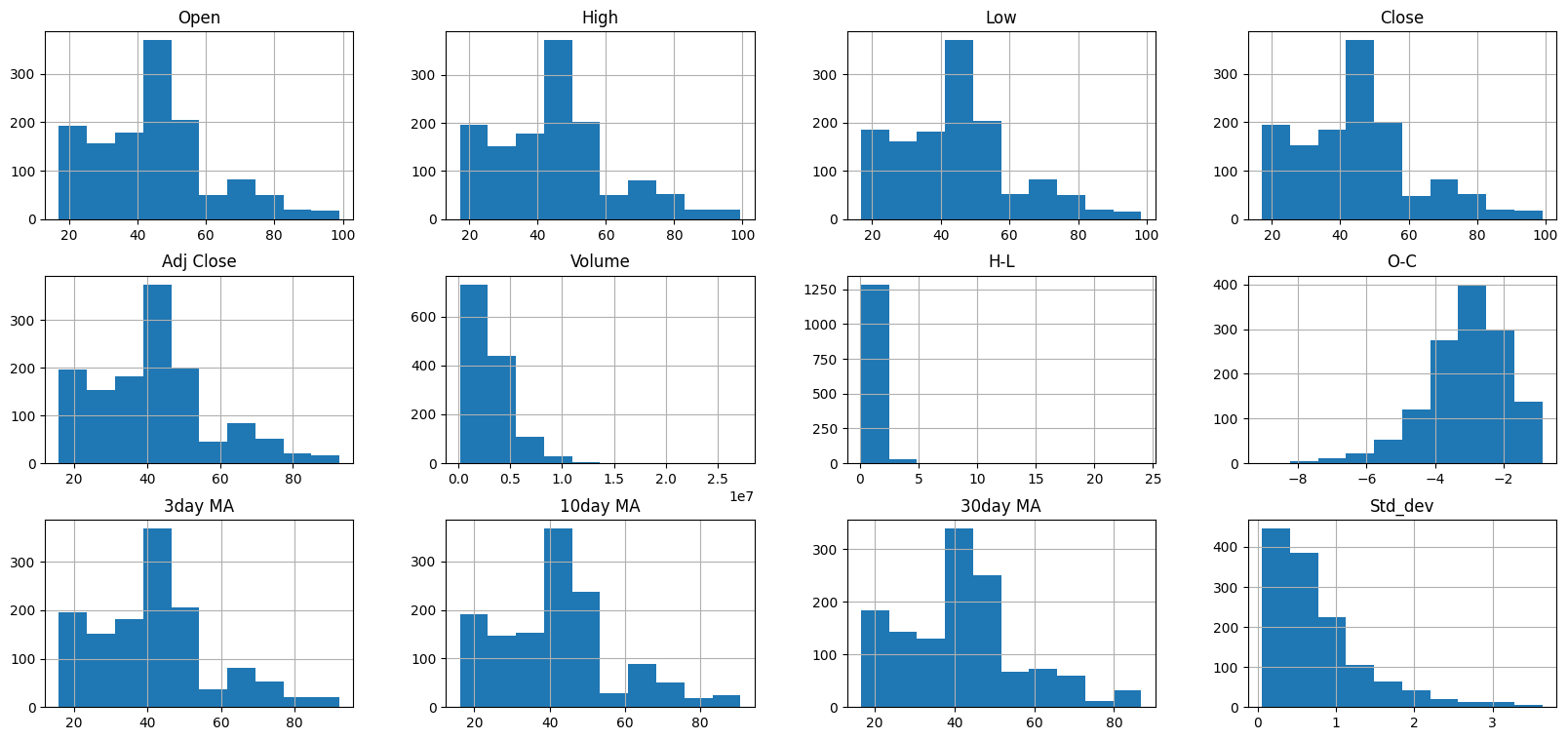
在这里插入图片描述

6.特征值分布

# 直方图

columns_multi = [x for x in list(df.columns)]
df.hist(layout = (3,4), column = columns_multi)
# 一种不常用的调整画布大小的方法
fig=plt.gcf()
fig.set_size_inches(20,9)

在这里插入图片描述

# 密度图

names = columns_multi
df.plot(kind='density', subplots=True, layout=(3,4), sharex=False)

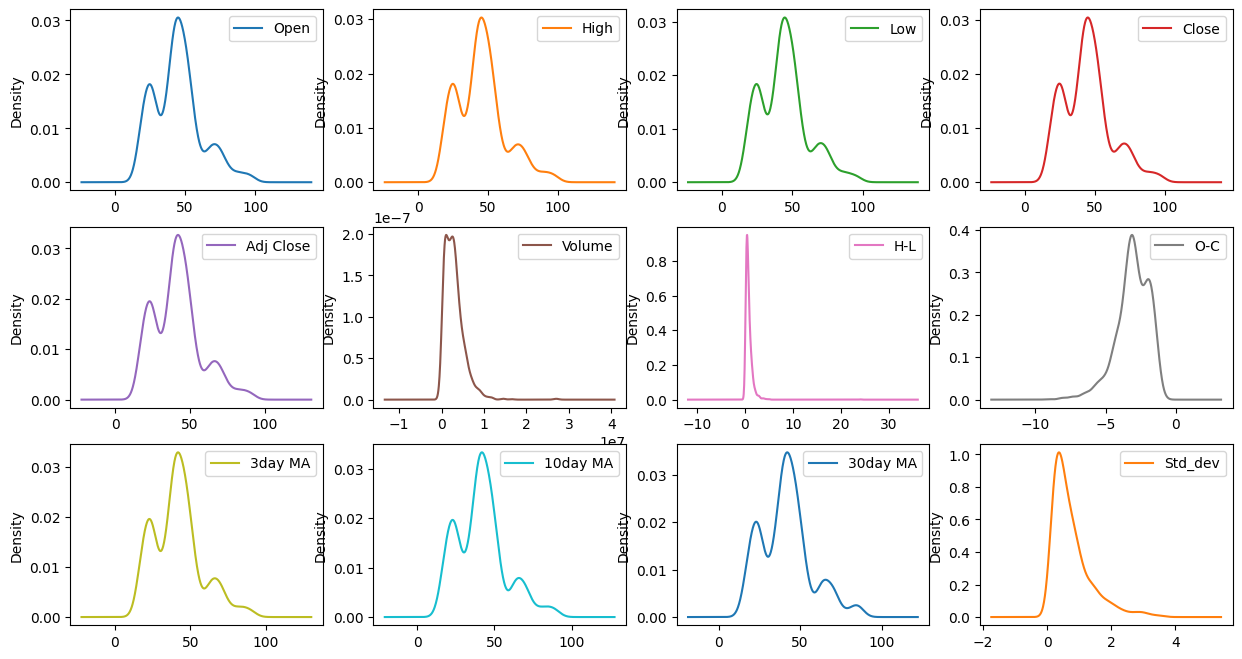
在这里插入图片描述

7.特征间的分布

# 函数可视化探索数据特征间的关系

sns.pairplot(df, size=3, diag_kind="kde")

在这里插入图片描述

8.特征重要性

通过多种方式对特征重要性进行评估，将每个特征的特征重要的得分取均值，最后以均值大小排序绘制特征重要性排序图，直观查看特征重要性。

from sklearn.feature_selection import RFE,RFECV,f_regression
from sklearn.linear_model import LinearRegression,Ridge,Lasso,LarsCV
from stability_selection import StabilitySelection,RandomizedLasso
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import seaborn as sns

8.1线性回归系数大小排序

回归系数(regression coefficient)在回归方程中表示自变量 对因变量 影响大小的参数。回归系数越大表示 x对 y 影响越大。

# 创建排序函数
df = df.dropna()
Y = df['Adj Close'].values
X = df.values
colnames = df.columns

# 定义字典来存储的排名
ranks = {}
# 创建函数，它将特征排名存储到rank字典中
def ranking(ranks, names, order=1):
    minmax = MinMaxScaler()
    ranks = minmax.fit_transform(
          order*np.array([ranks]).T).T[0]
    ranks = map(lambda x: round(x,2), ranks)
    res = dict(zip(names, ranks))
    return res

# 多个回归模型系数排序
import numpy as np

colnames = df.columns
# 使用线性回归
lr = LinearRegression()
lr.fit(X,Y)
ranks["LinReg"] = ranking(np.abs(lr.coef_), colnames)
# 使用 Ridge 
ridge = Ridge(alpha = 7)
ridge.fit(X,Y)
ranks['Ridge'] = ranking(np.abs(ridge.coef_), colnames)
# 使用 Lasso
lasso = Lasso(alpha=.05)
lasso.fit(X, Y)
ranks["Lasso"] = ranking(np.abs(lasso.coef_), colnames)

8.2随机森林特征重要性排序

随机森林得到的特征重要性的原理是我们平时用的较频繁的一种方法，无论是对分类型任务还是连续型任务，都有较好对效果。在随机森林中某个特征X的重要性的计算方法如下：

8.2.1连续型特征重要性

对于连续型任务的特征重要性，可以使用回归模型RandomForestRegressor中feature_importances_属性。

X_1 = df[['Open', 'High', 'Low', 'Close', 'Volume', 'H-L',
       'O-C', '3day MA', '10day MA', '30day MA', 'Std_dev']]
y_1 = df['Adj Close']

# 创建决策树分类器对象
clf = RandomForestRegressor(random_state=0, n_jobs=-1)
# 训练模型
model = clf.fit(X_1, y_1)
# 计算特征重要性
importances = model.feature_importances_
# 按降序排序特性的重要性
indices = np.argsort(importances)[::-1]
# 重新排列特性名称，使它们与已排序的特性重要性相匹配
names = [X_1.columns[i] for i in indices]

# 创建画布
plt.figure(figsize=(10,6))
# 添加标题
plt.title("Feature Importance")
# 添加柱状图
plt.bar(range(X_1.shape[1]), importances[indices])
# 为x轴添加特征名
plt.xticks(range(X_1.shape[1]), names, rotation=90)

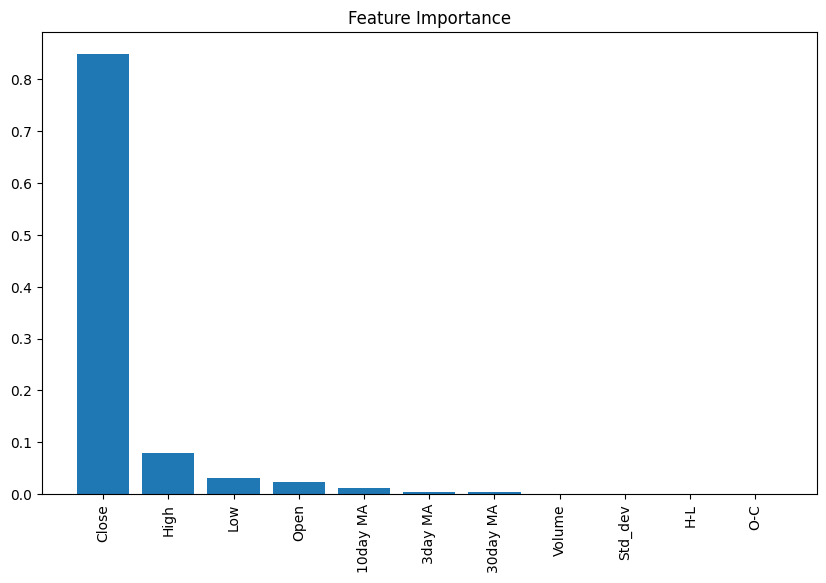
在这里插入图片描述

8.2.2分类型特征重要性

当该任务是分类型，需要用分类型模型时，可以使用RandomForestClassifier中的feature_importances_属性。

X_1 = df[['Open', 'High', 'Low', 'Close', 'Volume', 'H-L',
       'O-C', '3day MA', '10day MA', '30day MA', 'Std_dev']]
y_1 = df['Adj Close']

# 创建决策树分类器对象(没有分类变量，跳过演示)
# clf = RandomForestClassifier(random_state=0, n_jobs=-1)
clf = RandomForestRegressor(random_state=0, n_jobs=-1)

# 训练模型
model = clf.fit(X_1, y_1)
# 计算特征重要性
importances = model.feature_importances_
# 按降序排序特性的重要性
indices = np.argsort(importances)[::-1]
# 重新排列特性名称，使它们与已排序的特性重要性相匹配
names = [X_1.columns[i] for i in indices]

# 创建画布
plt.figure(figsize=(10,6))
# 添加标题
plt.title("Feature Importance")
# 添加柱状图
plt.bar(range(X_1.shape[1]), importances[indices])
# 为x轴添加特征名
plt.xticks(range(X_1.shape[1]), names, rotation=90)

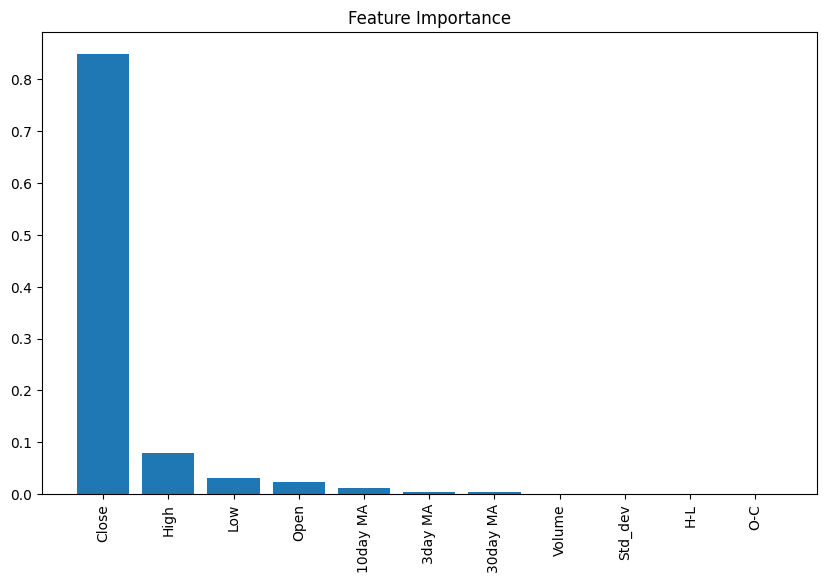
在这里插入图片描述

9.特征重要性：更高级的方法进行特征选择

下面两个顶层特征选择算法，之所以叫做顶层，是因为他们都是建立在基于模型的特征选择方法基础之上的，例如回归和SVM，在不同的子集上建立模型，然后汇总最终确定特征得分。

9.1RandomizedLasso方法

9.1.1RandomizedLasso的选择稳定性方法排序。

稳定性选择是一种基于二次抽样和选择算法相结合较新的方法，选择算法可以是回归、SVM或其他类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法，不断的重复，最终汇总特征选择结果，比如可以统计某个特征被认为是重要特征的频率（被选为重要特征的次数除以它所在的子集被测试的次数）。理想情况下，重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数，而最无用的特征得分将会接近于0。

import warnings
warnings.filterwarnings("ignore")

X_1 = df.values
colnames = df.columns
y_1 = df['Adj Close']

lambda_grid = np.linspace(0.001, 0.5, num=100)
rlasso = RandomizedLasso(alpha=0.04)

selector = StabilitySelection(base_estimator=rlasso, lambda_name='alpha',
                              lambda_grid=lambda_grid, threshold=0.9, verbose=1)
selector.fit(X_1, y_1)
# 运行随机Lasso的选择稳定性方法
ranks["rlasso/Stability"] = ranking(np.abs(selector.stability_scores_.max(axis=1)), colnames)
print('finished')

9.1.2稳定性得分可视化

import seaborn as sns
from stability_selection import *

fig, ax = plot_stability_path(selector)
fig.set_size_inches(15,6)
fig.show()

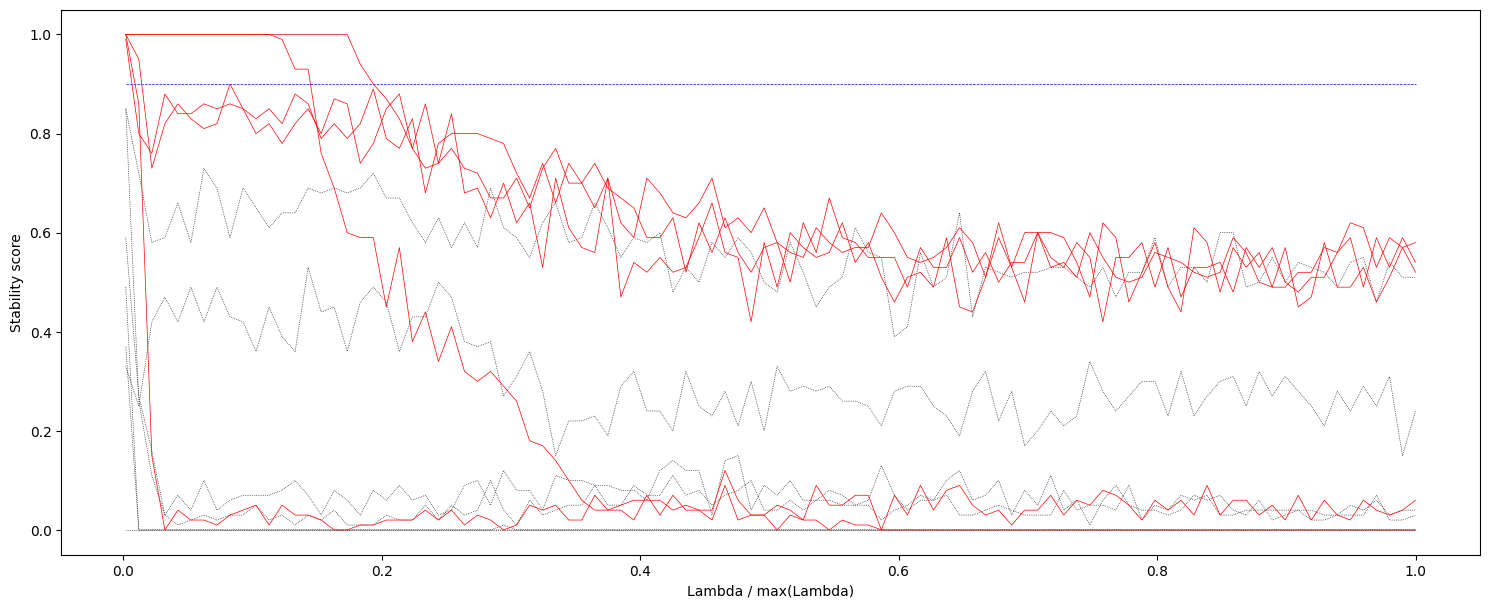
在这里插入图片描述

9.1.3查看得分超过阈值的变量索引及其得分

# 获取所选特征的掩码或整数索引
selected_variables = selector.get_support(indices=True)
selected_scores = selector.stability_scores_.max(axis=1)
print('Selected variables are:')
print('-----------------------')
for idx, (variable, score) in enumerate(
                zip(selected_variables, 
                    selected_scores[selected_variables])):
    print('Variable %d: [%d], score %.3f' % (idx + 1, variable, score))

Selected variables are:
-----------------------
Variable 1: [0], score 1.000
Variable 2: [1], score 0.990
Variable 3: [3], score 1.000
Variable 4: [7], score 1.000
Variable 5: [8], score 1.000

9.2 RFE递归特征消除特征排序

基于递归特征消除的特征排序。
给定一个给特征赋权的外部评估器(如线性模型的系数)，递归特征消除(RFE)的目标是通过递归地考虑越来越小的特征集来选择特征。

主要思想是反复的构建模型(如SVM或者回归模型)然后选出最好的(或者最差的)的特征(可以根据系数来选)。

  • 首先，在初始特征集上训练评估器，并通过任何特定属性或可调用属性来获得每个特征的重要性。
  • 然后，从当前的特征集合中剔除最不重要的特征。
  • 这个过程在训练集上递归地重复，直到最终达到需要选择的特征数。

这个过程中特征被消除的次序就是特征的排序。因此，这是一种寻找最优特征子集的贪心算法。

RFE的稳定性很大程度上取决于在迭代的时候底层用哪种模型。例如，假如RFE采用的普通的回归，没有经过正则化的回归是不稳定的，那么RFE就是不稳定的；假如采用的是Ridge，而用Ridge正则化的回归是稳定的，那么RFE就是稳定的。

X_1 = df.values
colnames = df.columns
y_1 = df['Adj Close']


lr = LinearRegression()
lr.fit(X_1,y_1)
# 当且仅当剩下最后一个特性时停止搜索
rfe = RFE(lr, n_features_to_select=1, verbose =3)
rfe.fit(X_1,y_1)
ranks["RFE"] = ranking(list(map(float, rfe.ranking_)),colnames, order=-1)

9.3RFECV递归特征消除交叉验证

Sklearn提供了 RFE 包，可以用于特征消除，还提供了 RFECV ，可以通过交叉验证来对的特征进行排序。

X_1 = df.values
colnames = df.columns
y_1 = df['Adj Close']


# 实例化估计器和特征选择器
svr_mod = SVR(kernel="linear")
rfecv = RFECV(svr_mod, cv=2)
print("实例化完毕")
# 训练模型
rfecv.fit(X_1, y_1)
print("训练完毕")
ranks["RFECV"] = ranking(list(map(float, rfecv.ranking_)), colnames, order=-1)
# Print support and ranking
print(rfecv.support_)
print(rfecv.ranking_)

实例化完毕
训练完毕
[ True  True False  True  True False False  True False False False False]
[1 1 2 1 1 8 3 1 7 5 6 4]

9.4 LarsCV最小角度回归模型(Least Angle Regression)交叉验证。

X_1 = df.values
colnames = df.columns
y_1 = df['Adj Close']

# 删除第二步中不重要的特征
# X = X.drop('sex', axis=1)
# 实例化
larscv = LarsCV(cv=5)
# 训练模型
larscv.fit(X_1, y_1)
ranks["LarsCV"] = ranking(list(map(float, larscv.coef_)), colnames, order=-1)
# 输出r方和估计alpha值
print(larscv.score(X_1, y_1))
print(larscv.alpha_)

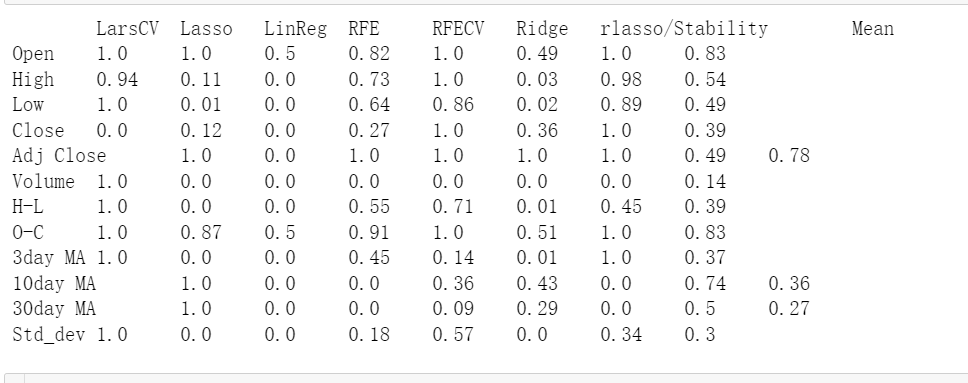
9.5 创建特征排序矩阵

创建一个空字典来存储所有分数，并求其平均值。

r = {}
for name in colnames:
    r[name] = round(np.mean([ranks[method][name] 
                             for method in ranks.keys()]), 2)
methods = sorted(ranks.keys())
ranks["Mean"] = r
methods.append("Mean")

print("\t%s" % "\t".join(methods))
for name in colnames:
    print("%s\t%s" % (name, "\t".join(map(str, 
                         [ranks[method][name] for method in methods]))))

在这里插入图片描述

9.6绘制特征重要性排序图

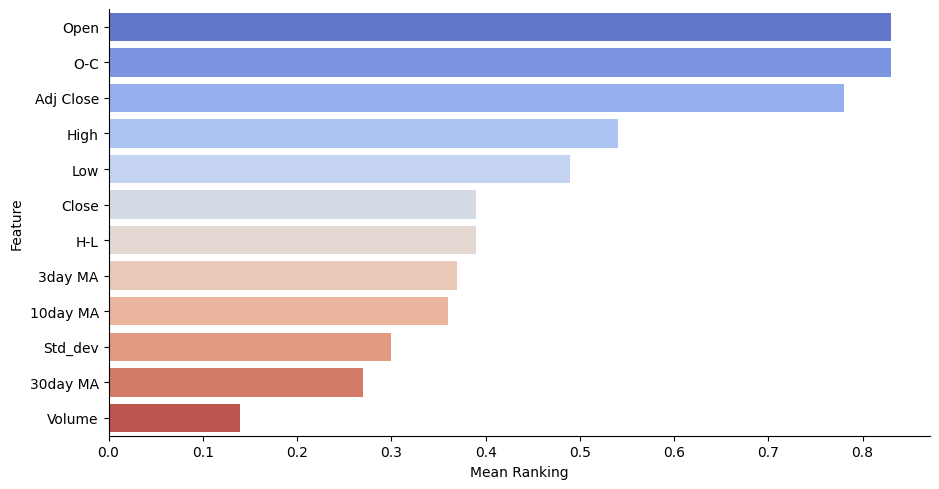
将平均得到创建DataFrame数据框，从高到低排序，并利用可视化方法将结果展示出。这样就一目了然，每个特征重要性大小。

meanplot = pd.DataFrame(list(r.items()), columns= ['Feature','Mean Ranking'])
# 排序
meanplot = meanplot.sort_values('Mean Ranking', ascending=False)
g=sns.catplot(x="Mean Ranking", y="Feature", data = meanplot, kind="bar", aspect=1.9, palette='coolwarm')

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/621814.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【MySQL数据库 | 番外篇】 聚合函数

【MySQL数据库 | 番外篇】 聚合函数

前言： 聚合函数是分组查询中一个重要的组成部分，想要利用分组查询，就要对聚合函数有不错的掌握，因此我们在这里开一篇番外，讲解SQL语法中的聚合函数 聚合函数： 聚合函数是SQL中一种特殊的函数，…
阅读更多...
大模型信息提取、文本生成、视觉语音应用

大模型信息提取、文本生成、视觉语音应用

448页新书《基础模型自然语言处理》，详述大模型在信息提取文本生成视觉语音应用。 Dr. Gerhard Paa 等人合著的《Foundation Models for Natural Language Processing》 一书系统介绍基础模型研究和应用的全面概述，而且是目前对此方面研究最新的综述。 …
阅读更多...
【Java】Java核心要点总结：59

【Java】Java核心要点总结：59

文章目录 1. 线程的run()和start()有什么区别，为什么不直接调用run()2. synchronized是什么，以及原理3. Java中如何实现多线程的通讯和协作4. Volatile有什么特点，为什么能够保证变量的可见性5. 为什么说synchronized是一个悲观锁&#xff0c…
阅读更多...
chatgpt赋能python：Python开发环境的下载方法

chatgpt赋能python：Python开发环境的下载方法

Python开发环境的下载方法 Python是一种高级的编程语言，受到广泛的社区和商业支持。它用于数据分析、人工智能和Web开发等领域，成为业界最流行的编程语言之一。搭建Python开发环境需要安装解释器、编辑器、包管理器和库，下面介绍Python开发环…
阅读更多...
chatgpt赋能python：用Python开发在线电影播放网站如何进行SEO

chatgpt赋能python：用Python开发在线电影播放网站如何进行SEO

用Python开发在线电影播放网站如何进行SEO 随着人们对于电影、电视剧等视频娱乐的需求日益增长，越来越多的在线电影播放网站涌现出来。作为开发者，如何通过搜索引擎优化（SEO）来使你的在线电影播放网站具有更好的可见度&#xff0…
阅读更多...
chatgpt赋能python：如何更新Python库？

chatgpt赋能python：如何更新Python库？

如何更新Python库？ Python语言已经成为现代编程语言中最受欢迎的一种，它的成功归功于它的灵活性、简洁性和可读性。Python库是它成功的关键，这些库是程序员的基本工具箱，可以更快地编写、测试和部署程序。 然而，Pyth…
阅读更多...
多分类问题

多分类问题

目录 多分类问题介绍1 多分类1.1 数据集1.2 数据可视化1.3 逻辑回归的向量化1.3.1 代价函数的向量化1.3.2 梯度的向量化1.3.3 正则化逻辑回归的向量化 1.4 多分类-分类器 1.5 使用分类器进行预测 多分类问题 介绍 在本练习中，我们将使用逻辑回归来识别手写数字&…
阅读更多...
python安装使用Flask框架（Vscode）

python安装使用Flask框架（Vscode）

编译器：VsCode，python3.** 首先安装，在终端输入 pip install flask安装成功后新建文件，app.python，创建一个简单的Web应用。 from flask import Flaskapp Flask(__name__)app.route(/) def hello():return Hello, …
阅读更多...
chatgpt赋能python：Python平均值命令在数据处理中的应用

chatgpt赋能python：Python平均值命令在数据处理中的应用

Python平均值命令在数据处理中的应用 Python是一门广泛应用于数据分析和数据处理的编程语言。在数据处理中，我们常常需要计算数据的平均值。Python中提供了多种方法来计算平均值，比如使用内置函数mean()或使用numpy库中的mean()函数等。本文将着重介绍P…
阅读更多...
Vue封装API，详细解释。

Vue封装API，详细解释。

1、为什么我们要封装API ps: 如果已经有了明确要封装API的需求，直接看第二步。 在没有封装API之前，我们是类似这样使用 axios 的 this.$axios.post(blogArticle/frontList,parms).then((resp) > { this.blogList resp.data, this.blogTota…
阅读更多...
【玩转Linux操作】Linux常用文件管理命令

【玩转Linux操作】Linux常用文件管理命令

🎊专栏【玩转Linux操作】 🍔喜欢的诗句：更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【Counting Stars 】 欢迎并且感谢大家指出小吉的问题🥰 目录 ​编辑 🎁ctrlc 🎁ctrlu 🎁t…
阅读更多...
chatgpt赋能python：Python平均分函数：简介和使用方法

chatgpt赋能python：Python平均分函数：简介和使用方法

Python平均分函数：简介和使用方法 如果您正在寻找如何计算Python中多个数字值的平均分数的方法，请继续阅读。本文将为您介绍Python中平均分函数的用途和使用方法。 什么是平均分函数？ Python的平均分函数是一个计算多个数字值的平均值的函…
阅读更多...
分享可以在线录音实时转写的方法

分享可以在线录音实时转写的方法

小伙伴们使用过录音记录吗？那知道录音实时转写吗？有没有听说过这个功能呢？它是可以通过语音识别技术，将录音中的信息快速转换为文本，并实现实时显示输出的功能。听起来是不是很有趣？而且它无需任何专业设备…
阅读更多...
线程，你是个什么？

线程，你是个什么？

线程的基本定义 线程（Thread）是操作系统能够进行运算调度的最小单位，它被包含在进程（Process）中，是进程中的实际运作单位。一个线程可以与同一进程中的其他线程共享进程的全部资源，包括内存、文…
阅读更多...
深入浅出讲解闭包及其原理

深入浅出讲解闭包及其原理

闭包 什么是闭包？ 闭包的概念并不复杂，但是它的定义比较绕（就像平时经常用到它，却又说不出来是什么）。可以在一个作用域中调用函数的内部函数并访问到该函数中的作用域的成员，这就是闭包。给一个建议&…
阅读更多...
springboot整合swagger3

springboot整合swagger3

目录 一、导入swagger3的依赖二、SwaggerConfig代码的解读三、整体代码四、访问swagger3 一、导入swagger3的依赖 <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</versi…
阅读更多...
【算法与数据结构】209.长度最小的子数组

【算法与数据结构】209.长度最小的子数组

文章目录 题目一、暴力穷解法二、滑动窗口法完整代码 所有的LeetCode题解索引&#xff0c;可以看这篇文章——【算法和数据结构】LeetCode题解。 题目 一、暴力穷解法 思路分析&#xff1a;这道题涉及到数组求和&#xff0c;那么我们很容易想到利用两个for循环来写&#xff0c;…
阅读更多...
【科技素养题】少儿编程 蓝桥杯青少组科技素养题真题及解析第20套

【科技素养题】少儿编程 蓝桥杯青少组科技素养题真题及解析第20套

少儿编程 蓝桥杯青少组科技素养题真题及解析第20套 1、“唐纳德特朗普 (Donald Trump) 曾经是美国总统”是一个 ()，“特朗普关于新冠肺炎疫情的不实言论”是一个 ()。 A、事实;事实 B、观点;事实 C、观点;观点 D、事实;观点 答案：D 考点分析：主要考查小朋友们对时事的…
阅读更多...
ChatGPT的未来发展

ChatGPT的未来发展

文章目录 1.什么是ChatGPT2.ChatGPT的基础技术3.ChatGPT工作原理4.ChatGPT应用场景5.ChatGPT局限性6.ChatGPT的未来发展 ✍创作者&#xff1a;全栈弄潮儿 &#x1f3e1; 个人主页&#xff1a; 全栈弄潮儿的个人主页 &#x1f3d9;️ 个人社区&#xff0c;欢迎你的加入&#xff…
阅读更多...
【严重】vm2 ＜3.9.18 沙箱逃逸漏洞（存在POC）

【严重】vm2 ＜3.9.18 沙箱逃逸漏洞（存在POC）

漏洞描述 vm2 是一个基于 Node.js 的沙箱环境&#xff0c;可以使用列入白名单的 Node 内置模块运行不受信任的代码&#xff0c;代理对象用于拦截并重定义宿主对象的各种操作。 vm2 3.9.18之前版本中&#xff0c;由于 prepareStackTrace 函数直接由 V8 引擎调用&#xff0c;其…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023