文章目录
- 题目
- 一、暴力穷解法
- 二、滑动窗口法
- 完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
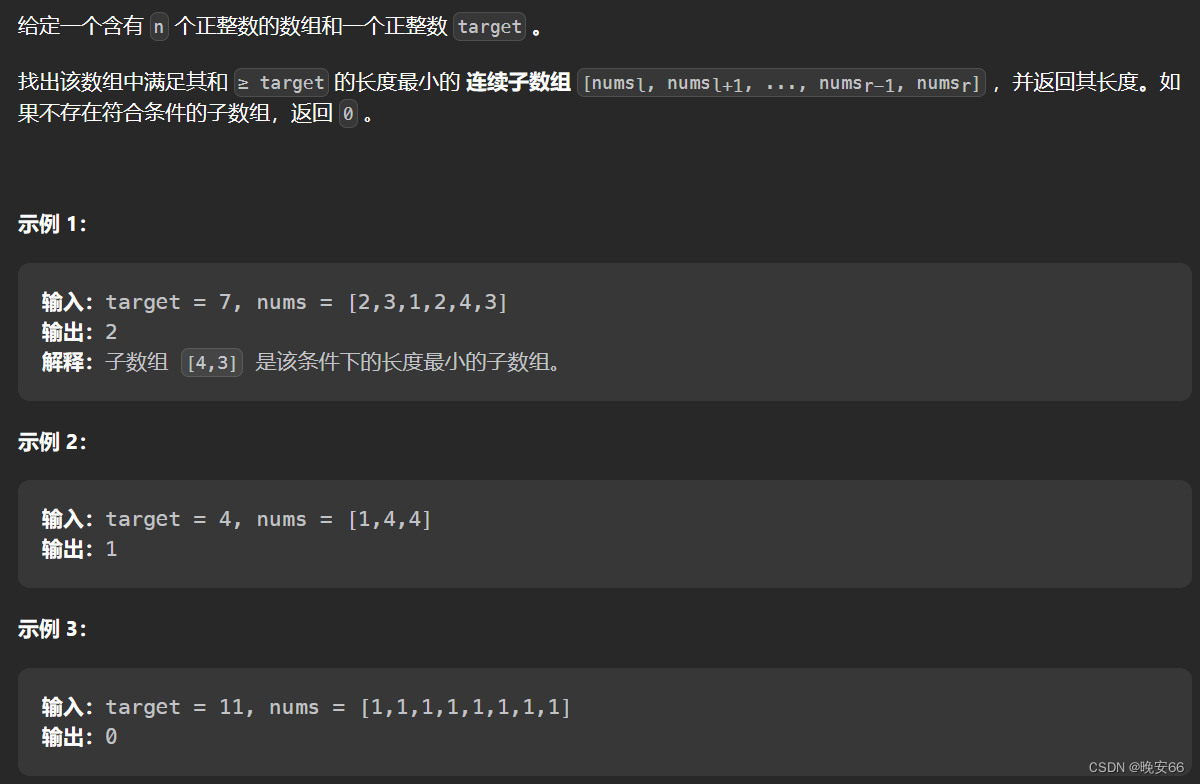
题目
一、暴力穷解法
思路分析:这道题涉及到数组求和,那么我们很容易想到利用两个for循环来写,第一个循环控制开始索引,第二个循环控制结束索引,当大于目标值时就计算子序列长度,我们通过两个索引计算,然后判断和上一个最短子序列长度相比较,如果更短就更新最短长度。
程序如下:
// 暴力穷解
int minSubArrayLen2(int target, vector<int>& nums) {
int result = INT32_MAX; // int32 类型最大整数
int sum = 0; // 子序列之和
int SubLen = 0;
for (int begin = 0; begin < nums.size(); begin++) {
sum = 0;
for (int end = begin; end < nums.size(); end++) {
sum += nums[end];
if (sum >= target) {
SubLen = end - begin + 1;
// 当前子序列的长度小于result(上一个最短子序列长度)时,更新,否则不变。
result = SubLen < result ? SubLen : result;
break;
}
}
}
return result == INT32_MAX ? 0 : result; // 如果没有变化,说明没有满足条件的子序列
}
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),用了两个for循环上,放到LeetCode上超时了。
- 空间复杂度: O ( 1 ) O(1) O(1)。
二、滑动窗口法
思路分析:我们可以想到子序列求和,类似于加窗然后累加这个操作,因此把这个办法叫做滑动窗口法。那么怎么设计窗口呢?==借助于双指针的思想,我们设置起始和终止指针。终止指针不断累加,当和大于目标值,进入for循环,去掉起始指针所在的值,且起始指针++,从而形成新的窗口,进入下一轮的判断。==最终得到最短子序列长度。
程序如下:
// 双指针法/滑动窗口法
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX; // int32 类型最大整数
int sum = 0; // 子序列之和
int SubLen = 0;
int begin = 0;
for (int end = 0; end < nums.size(); end++) {
sum += nums[end];
while (sum >= target) {
SubLen = end - begin + 1;
result = SubLen < result ? SubLen : result; // 当前子序列的长度小于result(上一个最短子序列长度)时,更新,否则不变。
sum -= nums[begin++];
}
}
return result == INT32_MAX ? 0 : result; // 如果没有变化,说明没有满足条件的子序列
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
完整代码
// 209.LeetCode长度最小的子数组
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
// 暴力穷解
int minSubArrayLen2(int target, vector<int>& nums) {
int result = INT32_MAX; // int32 类型最大整数
int sum = 0; // 子序列之和
int SubLen = 0;
for (int begin = 0; begin < nums.size(); begin++) {
sum = 0;
for (int end = begin; end < nums.size(); end++) {
sum += nums[end];
if (sum >= target) {
SubLen = end - begin + 1;
result = SubLen < result ? SubLen : result; // 当前子序列的长度小于result(上一个最短子序列长度)时,更新,否则不变。
break;
}
}
}
return result == INT32_MAX ? 0 : result; // 如果没有变化,说明没有满足条件的子序列
}
// 双指针法/滑动窗口法
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX; // int32 类型最大整数
int sum = 0; // 子序列之和
int SubLen = 0;
int begin = 0;
for (int end = 0; end < nums.size(); end++) {
sum += nums[end];
while (sum >= target) {
SubLen = end - begin + 1;
result = SubLen < result ? SubLen : result; // 当前子序列的长度小于result(上一个最短子序列长度)时,更新,否则不变。
sum -= nums[begin++];
}
}
return result == INT32_MAX ? 0 : result; // 如果没有变化,说明没有满足条件的子序列
}
};
void my_print(vector<int> & nums, string str) {
cout << str << endl;
for (vector<int>::iterator it = nums.begin(); it < nums.end(); it++) {
cout << *it << ' ';
}
cout << endl;
}
int main()
{
int target = 7;
int arr[] = { 2,3,1,2,4,3 };
//int target = 11;
//int arr[] = { 1,1,1,1,1,1,1,1 };
vector<int> nums;
Solution s1;
for (int i = 0; i < sizeof(arr) / sizeof(int); i++){
nums.push_back(arr[i]);
}
my_print(nums, "目标数组:");
int sublength = s1.minSubArrayLen(target, nums);
cout << "满足条件的最短子数组长度:" << endl <<sublength << endl;
system("pause");
return 0;
}
end