引言

逻辑斯谛回归(logistic regression)是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型(maximum entropy model)。

由于后面最优化方法中用到了最优化理论中的一些知识，建议先阅读最优化简介。

逻辑斯谛回归模型

定义 6.1(逻辑斯谛分布) 设$X$施连续随机变量，$X$服从逻辑斯谛分布是指$X$具有下列分布函数和密度函数：
$$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu )/\gamma }}\text{\hspace{1em}(6.1)}$$

$$f(x)=F^{\prime }(x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/\gamma })}\text{\hspace{1em}(6.2)}$$

其中，$\mu$为位置参数，$\gamma >0$为形状参数。

这里推导一下$f(x)$。
$$\begin{array}{rl}{F}^{\prime }(x)& ={\left(\frac{1}{1+e^{-(x-\mu )/\gamma }}\right)}^{\prime }\\ & =-\frac{d(1+e^{-(x-\mu )/\gamma })/dx}{(1+e^{-(x-\mu )/\gamma }{)}^2}\\ & =-\frac{e^{-(x-\mu )/\gamma }\cdot -\frac{1}{\gamma }}{(1+e^{-(x-\mu )/\gamma }{)}^2}\\ & =\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/\gamma }{)}^2}\end{array}$$
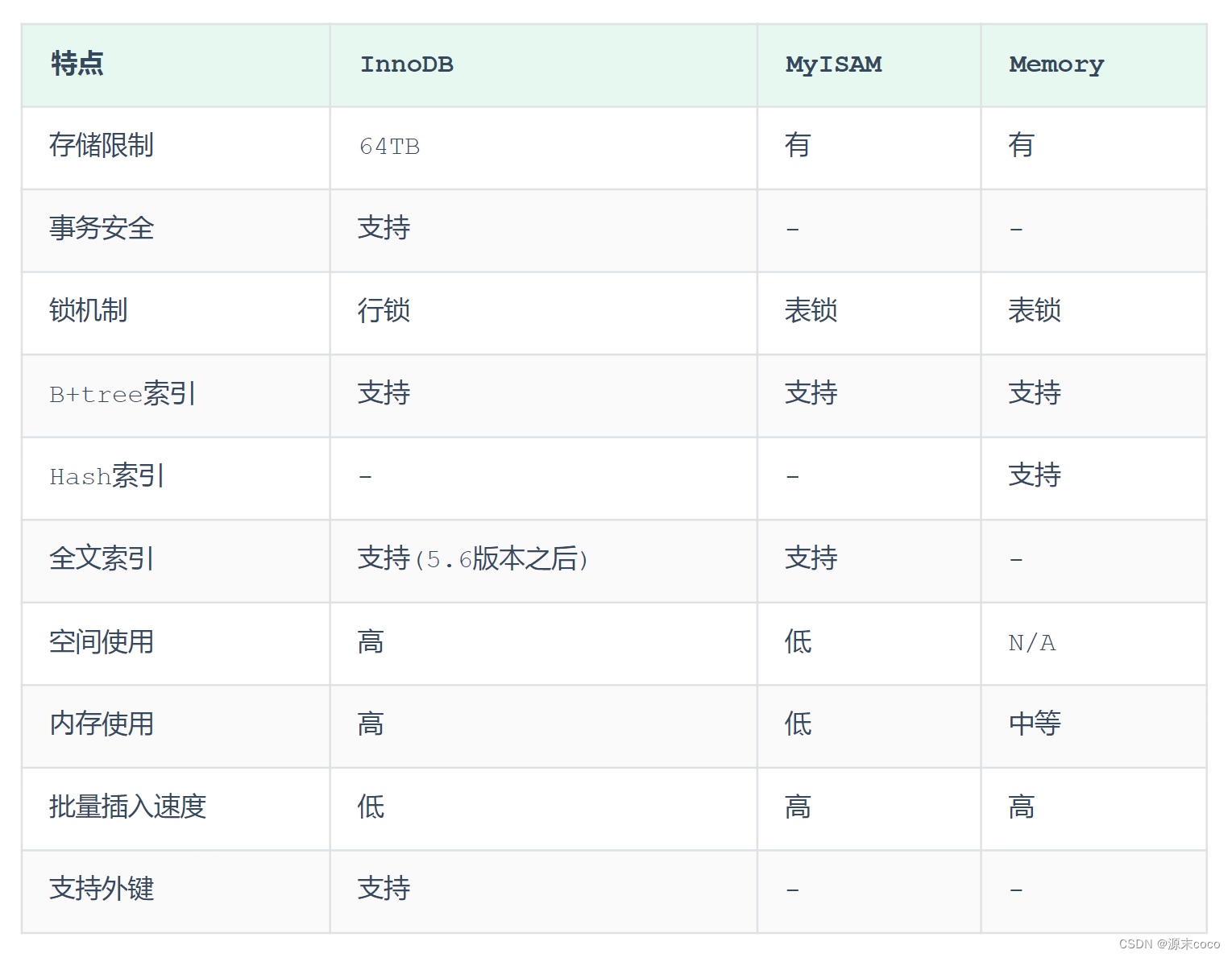
逻辑斯谛分布的密度函数$f(x)$和分布函数$F(x)$的图形如图6.1所示。分布函数属于逻辑斯谛函数，其图形式一条S形曲线。该曲线以点$(\mu ,\frac{1}{2})$为中心对称，即满足
$$F(-x+\mu )-\frac{1}{2}=-F(x+\mu )+\frac{1}{2}$$

二项逻辑斯谛回归模型

二项逻辑斯谛回归模型(binomial logistic regression model)是一种分类模型，由条件概率分布$P(Y|X)$表示，形式为参数化的逻辑斯谛分布。

随机变量$X$取值为实数，随机变量$Y$的取值为$1$或$0$。

定义6.2(逻辑斯谛回归模型) 二项逻辑斯谛回归模型是如下的条件概率分布：
$$P(Y=1|X)=\frac{\exp (w\cdot x+b)}{1+\exp (w\cdot x+b)}\text{\hspace{1em}(6.3)}$$

$$P(Y=0|X)=\frac{1}{1+\exp (w\cdot x+b)}\text{\hspace{1em}(6.4)}$$

其中，$x\in {\mathbb{R}}^n$是输入， Y ∈ { 0 , 1 } Y\in \{0,1\} Y∈{0,1}是输出，$w\in {\mathbb{R}}^n$和$b\in \mathbb{R}$是参数，$w$称为权值向量，$b$称为偏置，$w\cdot x$为$w$和$x$的内积。

对于给定的输入实例$x$，按照上面两式分别求得属于$Y=1$和$Y=0$的概率，然后比较两个概率的大小，将实例$x$分为概率值较大的那一类。

为了方便，即消掉偏置$b$，有时将权值向量和输入向量加以扩充，仍然记作$w,x$，此时$w=(w^{(1)},w^{(2)}\cdots ,w^{(n)},b{)}^T,x=(x^{(1)},x^{(2)}\cdots ,x^{(n)},1{)}^T$。

此时，逻辑斯谛回归模型可以写成如下形式：
$$P(Y=1|X)=\frac{\exp (w\cdot x)}{1+\exp (w\cdot x)}\text{\hspace{1em}(6.5)}$$

$$P(Y=0|X)=\frac{1}{1+\exp (w\cdot x)}\text{\hspace{1em}(6.6)}$$

一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果记事件发生的概率为$p$，那么该事件的几率是$\frac{p}{1-p}$，该事件的对数几率(log odds)或logit函数为
$$\text{logit}(p)=\log \frac{p}{1-p}$$
对于逻辑斯谛回归而言，由式$(6.5)$与式$(6.6)$得
$$\log \frac{P(Y=1|x)}{1-P(Y=1|x)}=\log \frac{\exp (w\cdot x)}{1}=w\cdot x$$
也就是说，在逻辑斯谛回归模型中，输出$Y=1$的对数几率是输入$x$的线性函数表示的模型，即逻辑斯谛回归模型。

模型参数估计

逻辑斯谛回归模型学习中，对于给定的训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$，可以应用极大似然估计法估计模型参数，从而得到逻辑斯谛回归模型。

设：
$$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$$
似然函数为
$$\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}$$
对数似然函数为
$$\begin{array}{rl}L(w)& =\sum _{i=1}^N[y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i))]\\ & =\sum _{i=1}^N\left[y_i\log \pi (x_i)+\log (1-\pi (x_i)-y_i\log (1-\pi (x_i)\right]\\ & =\sum _{i=1}^N\left[y_i\log \frac{\pi (x_i)}{1-\pi (x_i)}+\log (1-\pi (x_i))\right]\\ & =\sum _{i=1}^N\left[y_i(w\cdot x_i)+\log (\frac{1}{1+\exp (w\cdot x_i)})\right]\\ & =\sum _{i=1}^N[y_i(w\cdot x_i)-\log (1+\exp (w\cdot x_i))]\end{array}$$
对$L(w)$求极大值，得到$w$的估计值。

这样，问题就变成了以对数似然函数为目标函数的最优化问题。

假设$w$的极大似然估计是$\hat{w}$，那么学到的逻辑斯谛回归模型为
$$\begin{gathered} P(Y=1|X)=\frac{\exp (\hat{w}\cdot x)}{1+\exp (\hat{w}\cdot x)} \\ P(Y=0|X)=\frac{1}{1+\exp (\hat{w}\cdot x)} \end{gathered}$$

多项逻辑斯谛回归

上面介绍的逻辑斯谛回归模型用于二分类，可以将其推广为多项逻辑斯谛回归模型(multi-nominal logistic regression model)，用于多分类。

假设离散型随机变量$Y$的取值集合是 { 1 , 2 , ⋯   , K } \{1,2,\cdots,K\} {1,2,⋯,K}，那么多项逻辑斯谛回归模型是
$$P(Y=k|x)=\frac{\exp (w_k\cdot x)}{1+{\sum }_{k=1}^{K-1}\exp (w_k\cdot x)},k=1,2,\cdots ,K-1\text{\hspace{1em}(6.7)}$$
这里也分成了两部分，上面是$k$为$1$到$K-1$的部分，那么为了保证概率和为$1$，$P(Y=K|x)=1-{\sum }_{k=1}^{K-1}P(Y=k|x)$：
$$P(Y=K|x)=\frac{1}{1+{\sum }_{k=1}^{K-1}\exp (w_k\cdot x)}$$

最大熵模型

最大熵原理

最大熵原理是概率模型学习的一个准则。最大熵原理认为，学习概率模型时，在所有可能的概率模型分布中，熵最大的模型就是最好的模型。

通常用约束条件来确定概率模型的集合，所以，最大熵原理也可以表述为在满足约束条件的模型集合汇总选取熵最大的模型。

假设离散随机变量$X$的概率分布式$P(X)$，则其熵是
$$H(P)=-\sum _{x}P(x)\log P(x)\text{\hspace{1em}(6.9)}$$

熵的公式可以参考一文弄懂信息熵。

熵满足下列不等式：
$$0\le H(P)\le \log |X|$$
其中，$|X|$是$X$的取值个数，当且仅当$X$的分布式均匀分布时$H(P)=\log |X|$。即，当$X$服从均匀分布时，熵最大。

最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分都是“等可能的”。最大熵原理通过熵的最大化来表示等可能性。

下面，通过一个例子来介绍一下最大熵原理。

例 6.1 假设随机变量$X$有5个取值 { A , B , C , D , E } \{A,B,C,D,E\} {A,B,C,D,E}，要估计各个值的概率$P(A),P(B),P(C),P(D),P(E)$。

解 这些概率值满足以下约束条件：
$$P(A)+P(B)+P(C)+P(D)+P(E)=1$$
满足这个约束条件的概率分布有无穷多个。如果没有任何其他信息，一个办法就是认为这个分布中取各个值的概率都是相等的：
$$P(A)=P(B)=P(C)=P(D)=P(E)=\frac{1}{5}$$
有时，能从一些先验知识中得到一些对概率值的约束条件，例如：
$$\begin{gathered} P(A)+P(B)=\frac{3}{10} \\ P(A)+P(B)+P(C)+P(D)+P(E)=1 \end{gathered}$$
满足这两个约束条件的概率分布仍然有无穷多个。在缺少其他信息的情况下，可以认为$A$与$B$是等概率的，$C,D,E$是等概率的，于是，
$$\begin{gathered} P(A)=P(B)=\frac{3}{20} \\ P(C)=P(D)=P(E)=\frac{7}{30} \end{gathered}$$
如果还有第3个约束条件：
$$\begin{gathered} P(A)+P(C)=\frac{1}{2} \\ P(A)+P(B)=\frac{3}{10} \\ P(A)+P(B)+P(C)+P(D)+P(E)=1 \end{gathered}$$
可以继续安装满足约束条件下求等概率的方法估计概率分布。这里稍微复杂一点，可以让$P(B),P(C),P(D),P(E)$都用$P(A)$来表示，最终计算出$P(A)$。

最大熵模型的定义

最大熵原理应用到分类得到最大熵模型。

假设分类模型是一个条件概率分布$P(Y|X)$，$X\in \mathcal{X}\subseteq {\mathbb{R}}^n$表示输入，$Y\in \mathcal{Y}$表示输出，$\mathcal{X}$和$\mathcal{Y}$分别是输入和输出的集合。这个模型表示的是对于给定的输入$X$，以条件概率$P(Y|X)$输出$Y$。

给定一个训练数据集
$$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$
学习的目标是用最大熵原理选择最好的分类模型。

首先考虑模型应该满足的条件。给定训练数据集，可以确定联合分布$P(X,Y)$的经验分布和边缘分布$P(X)$的经验分布，分别以$\tilde{P}(X,Y)$和$\tilde{P}(X)$表示。这两个经验分布计算如下：
$$\begin{gathered} \tilde{P}(X=x,Y=y)=\frac{v(X=x,Y=y)}{N} \\ \tilde{P}(X=x)=\frac{v(X=x)}{N} \end{gathered}$$
其中，$v(X=x,Y=y)$表示训练数据中样本$(x,y)$出现的频数，$v(X=x)$表示输入$x$出现的频数，$N$表示训练样本总量。

用特征函数(feature function)$f(x,y)$描述输入$x$和输出$y$之间的某一个事实。其定义是
$$f(x,y)=\{\begin{array}{lr}1,& x与y满足某一事实\\ 0,& 否则\end{array}$$
当$x,y$满足这个事实时区直为$1$，否则取值为$0$。

特征函数$f(x,y)$关于经验分布$\tilde{P}(X,Y)$的期望值，用$E_{\tilde{P}}(f)$表示：
$$E_{\tilde{P}}(f)=\sum _{x,y}\tilde{P}(x,y)f(x,y)$$
特征函数$f(x,y)$关于模型$P(Y|X)$与经验分布$\tilde{P}(X)$的期望值，用$E_p(f)$表示：
$$E_P(f)=\sum _{x,y}P(x,y)f(x,y)=\sum _{x,y}P(x)P(y|x)f(x,y)=\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)$$
这里用$x$的经验分布$\tilde{P}(x)$来代替真实分布$P(x)$。

我们无法保证训练数据集得到的经验分布和真实分布完全相同，但我们可以假设它们的期望相同，即
$$E_P(f)=E_{\tilde{P}}(f)\text{\hspace{1em}(6.10)}$$
或者说
$$\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)=\sum _{x,y}\tilde{P}(x,y)f(x,y)\text{\hspace{1em}(6.11)}$$
我们将式$(6.10)$或$(6.11)$作为模型学习的约束条件。假设有$n$个特征函数$f_i(x,y),i=1,2,\cdots ,n$，那么就有$n$个约束条件。

定义6.3 (最大熵模型) 假设满足所有约束条件的模型集合为
C ≡ { P ∈ P ∣ E p ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯   , n } (6.12) \mathcal C \equiv \{ P \in \mathcal P| E_p(f_i)=E_{\tilde P}(f_i),\quad i=1,2,\cdots,n \} \tag{6.12} C≡{P∈P∣Ep​(fi​)=EP~​(fi​),i=1,2,⋯,n}(6.12)
那么定义在条件概率分布$P(Y|X)$上的条件熵为
$$H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)\text{\hspace{1em}(6.13)}$$
则模型集合$\mathcal{C}$中条件熵$H(P)$最大的模型称为最大熵模型，式中的对数为自然对数。

条件熵$H(Y|X=x)$为变量$Y$在变量$X$取特定值$x$条件下的熵，那么$H(Y|X)$就是$H(Y|X=x)$在$X$取遍所有可能的$x$后取平均的结果。

给定随机变量$X$和$Y$，取值分别为$\mathcal{X}$和$\mathcal{Y}$，在给定$X$条件下$Y$的条件熵定义为：
$$\begin{array}{rl}H(Y|X)& =\sum _{x\in \mathcal{X}}p(x)H(Y|X=x)\\ & =-\sum _{x\in \mathcal{X}}p(x)\sum _{y\in \mathcal{Y}}p(y|x)\log p(y|x)\\ & =-\sum _{x\in \mathcal{X}}\sum _{y\in \mathcal{Y}}p(x)p(y|x)\log p(y|x)\\ & =-\sum _{x\in \mathcal{X},y\in \mathcal{Y}}p(x)p(y|x)\log p(y|x)\end{array}$$
用$x$的经验分布$\tilde{P}(x)$来代替真实分布$P(x)$，就得到了$(6.13)$。

最大熵模型的学习

最大熵模型的学习过程就是求解最大熵模型的过程。最大熵模型的学习可以形式化为约束最优化问题。

对于给定的训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$以及特征函数$f_i(x,y),i=1,2,\cdots ,n$，最大熵模型的学习等价于约束最优化问题：
$$\begin{array}{rlrl}& \underset{P\in C}{\max }& & H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)\\ & \text{s.t.}& & E_P(f_i)=E_{\tilde{P}}(f_i),i=1,\dots ,n\\ & & & \sum _{y}P(y|x)=1\end{array}$$
我们倾向于最小化，所以将最大值问题改写为等价的求最小值问题：
$$\underset{P\in C}{\min }-H(P)=\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)\text{\hspace{1em}(6.14)}$$

$$\text{s.t.}{E}_P(f_i)-E_{\tilde{P}}(f_i)=0,i=1,\dots ,n\text{\hspace{1em}(6.15)}$$

$$\sum _{y}P(y|x)=1\text{\hspace{1em}(6.16)}$$

只要求解约束最优化问题$(6.14)\sim (6.16)$，所得出的解，就是最大熵模型学习的解。下面来推导一下。

根据补充知识，将约束最优化问题的原始问题转换为无约束最优化的对偶问题。通过求解对偶问题求解原始问题。

首先，引进拉格朗日乘子$w_0,w_1,\cdots ,w_n$，定义拉格朗日函数$L(P,w)$：
$$\begin{array}{rl}L(P,w)& \equiv -H(P)+w_0\left(1-\sum _{y}P(y|x)\right)+\sum _{i=1}^n{w}_i(E_{\tilde{P}}(f_i)-(E_P(f_i))\\ & =\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)+w_0\left(1-\sum _{y}P(y|x)\right)+\sum _{i=1}^n{w}_i\left(\sum _{x,y}\tilde{P}(x,y)f_i(x,y)-\sum _{x,y}\tilde{P}(x)P(y|x)f_i(x,y)\right)\end{array}\text{\hspace{1em}(6.17)}$$

最优化的原始问题是
$$\underset{P\in C}{\min }\underset{w}{\max }L(P,w)\text{\hspace{1em}(6.18)}$$
对偶问题是
$$\underset{w}{\max }\underset{P\in C}{\min }L(P,w)\text{\hspace{1em}(6.19)}$$
由于拉格朗日函数$L(P,w)$是$P$的凸函数，原始问题$(6.18)$的解与对偶问题$(6.19)$的解是等价的。这样可以通过求解对偶问题$(6.19)$来求解原始问题$(6.18)$。

这里暂时不证明这个拉格朗日函数是$P$的凸函数。

首先，求解对偶问题$(6.19)$内部的极小化问题${\min }_{P\in C}L(P,w)$。${\min }_{P\in C}L(P,w)$是$w$的函数，将其记作
$$\Psi (w)=\underset{P\in C}{\min }L(P,w)=L(P_w,w)\text{\hspace{1em}(6.20)}$$

$\Psi (w)$称为对偶函数。同时，将其解记作
$$P_w=\arg \underset{P\in C}{\min }L(P,w)=P_w(y|x)\text{\hspace{1em}(6.21)}$$
首先，求$L(P,w)$对$P(y|x)$的偏导数
$$\begin{array}{rl}\frac{\partial L(P,w)}{\partial P(y|x)}& =\sum _{x,y}\tilde{P}(x)(\log P(y|x)+1)-\sum _y{w}_0-\sum _{x,y}\tilde{P}(x)\sum _{i=1}^n{w}_i{f}_i(x,y)\\ & =\sum _{x,y}\tilde{P}(x)\left(\log P(y|x)+1-w_0-\sum _{i=1}^n{w}_i{f}_i(x,y)\right)\end{array}$$
令偏导数等于0，在$\tilde{P}(x)>0$的情况下，上式可得
$$\begin{gathered} \log P(y|x)+1-w_0-\sum _{i=1}^n{w}_i{f}_i(x,y)=0 \\ \log P(y|x)=\sum _{i=1}^n{w}_i{f}_i(x,y)+w_0-1 \\ P(y|x)=\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)+w_0-1\right) \\ P(y|x)=\frac{\exp \left({\sum }_{i=1}^n{w}_i{f}_i(x,y)\right)}{\exp (1-w_0)} \end{gathered}$$
这样我们把最大熵问题转换成了计算$w_i$的问题，即与拉格朗日乘子有关。

再利用${\sum }_{y}P(y|x)=1$，把上式两边加上${\sum }_y$：
$$\begin{gathered} \sum _{y}P(y|x)=\frac{{\sum }_y\exp \left({\sum }_{i=1}^n{w}_i{f}_i(x,y)\right)}{{\sum }_y\exp (1-w_0)}=\frac{{\sum }_y\exp \left({\sum }_{i=1}^n{w}_i{f}_i(x,y)\right)}{\exp (1-w_0){\sum }_y} \\ \frac{{\sum }_y\exp \left({\sum }_{i=1}^n{w}_i{f}_i(x,y)\right)}{\exp (1-w_0)}=1\Rightarrow \exp (1-w_0)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right) \end{gathered}$$
上式这个$\exp (1-w_0)$的表达式我们计算出来了，就是所谓的规范化因子，改变$w$就得到了不同的函数，所以是和$w$有关的，而$y$已经被求和约掉了，只剩下参数$x$，记为$Z_w(x)$，称作规范化因子。

即
$$Z_w(x)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)\text{\hspace{1em}(6.22)}$$
把$Z_w(x)$代入到上面的$\exp (1-w_0)$，得到$P(y|x)$的表达式：
$$P_w(y|x)=\frac{1}{Z_w(x)}\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)\text{\hspace{1em}(6.23)}$$
不同的一组$w$会得到不同的概率分布，所以写成$P_w(y|x)$。

其中$f_i(x,y)$是特征函数；$w_i$对应的权重。

由式$(6.22)$和$(6.23)$表示的模型$P_w=P_w(y|x)$就是最大熵模型。这里$w$是最大熵模型中的参数向量。

所以，最大熵模型的学习，学的就是特征函数对应的权重。

之后，求解对偶问题外部的极大化问题
$$\underset{w}{\max }\Psi (w)\text{\hspace{1em}(6.24)}$$
将它的解记为$w^{\ast }$，即
$$w^{\ast }=\arg \underset{w}{\max }\Psi (w)\text{\hspace{1em}(6.25)}$$
此时，可以应用最优化算法求对偶函数$\Psi (w)$的极大化，得到$w^{\ast }$，用来表示$P^{\ast }\in \mathcal{C}$。

这里，$P^{\ast }=P_{w^{\ast }}=P_{w^{\ast }}(y|x)$是学习到的最优模型(最大熵模型)。

说明最大熵模型的学习归结为对偶函数$\Psi (w)$的极大化。

我们来看一个例题。

例 6.2 学习例6.1中的最大熵模型。

解 为了方便，分别以$y_1,y_2,y_3,y_4,y_5$表示$A,B,C,D,E$，于是最大熵模型学习的最优化问题是
$$\begin{array}{rlrl}& \min & & -H(P)=\sum _{i=1}^{5}P(y_i)\log P(y_i)\\ & \text{s.t.}& & P(y_1)+P(y_2)=\tilde{P}(y_1)+\tilde{P}(y_2)=\frac{3}{10}\\ & & & \sum _{i=1}^{5}P(y_i)=\sum _{i=1}^5\tilde{P}(y_i)=1\end{array}$$
这里我们要找到使得负熵最小的那个分布$P$。

引进拉格朗日乘子$w_0,w_1$，定义拉格朗日函数
$$L(P,w)=\sum _{i=1}^{5}P(y_i)\log P(y_i)+w_1\left(P(y_1)+P(y_2)-\frac{3}{10}\right)+w_0\left(\sum _{i=1}^{5}P(y_i)-1\right)$$
根据拉格朗日对偶性，可以通过求解对偶最优化问题得到原始最优化问题的解，所以求
$$\underset{w}{\max }\underset{P}{\min }L(P,w)$$
首先求解$L(P,w)$关于$P$的极小化问题。为此，固定$w_0,w_1$，求偏导数：
$$\begin{gathered} \frac{\partial L(P,w)}{\partial P(y_1)}=\log P(y_1)+1+w_1+w_0 \\ \frac{\partial L(P,w)}{\partial P(y_2)}=\log P(y_2)+1+w_1+w_0 \\ \frac{\partial L(P,w)}{\partial P(y_3)}=\log P(y_3)+1+w_0 \\ \frac{\partial L(P,w)}{\partial P(y_4)}=\log P(y_4)+1+w_0 \\ \frac{\partial L(P,w)}{\partial P(y_5)}=\log P(y_5)+1+w_0 \end{gathered}$$
令各偏导数等于0，解得
$$\begin{gathered} P(y_1)=P(y_2)=e^{-w_1-w_0-1} \\ P(y_3)=P(y_4)=P(y_5)=e^{-w_0-1} \end{gathered}$$
把它们代入到$L(P,w)$中，于是，
$$\underset{P}{\min }L(P,w)=L(P_w,w)=-2e^{-w_1-w_0-1}-3e^{-w_0-1}-\frac{3}{10}{w}_1-w_0$$
再求解$L(P_w,w)$关于$w$的极大化问题：
$$\underset{w}{\max }L(P_w,w)=-2e^{-w_1-w_0-1}-3e^{-w_0-1}-\frac{3}{10}{w}_1-w_0$$
分别求$L(P_w,w)$对$w_0,w_1$的偏导数并令其为0，得到
$$\begin{gathered} e^{-w_1-w_0-1}=\frac{3}{20} \\ {e}^{-w_0-1}=\frac{7}{30} \end{gathered}$$
于是得到所要求的概率分布为
$$\begin{gathered} P(y_1)=P(y_2)=\frac{3}{20} \\ P(y_3)=P(y_4)=P(y_5)=\frac{7}{30} \end{gathered}$$