题目

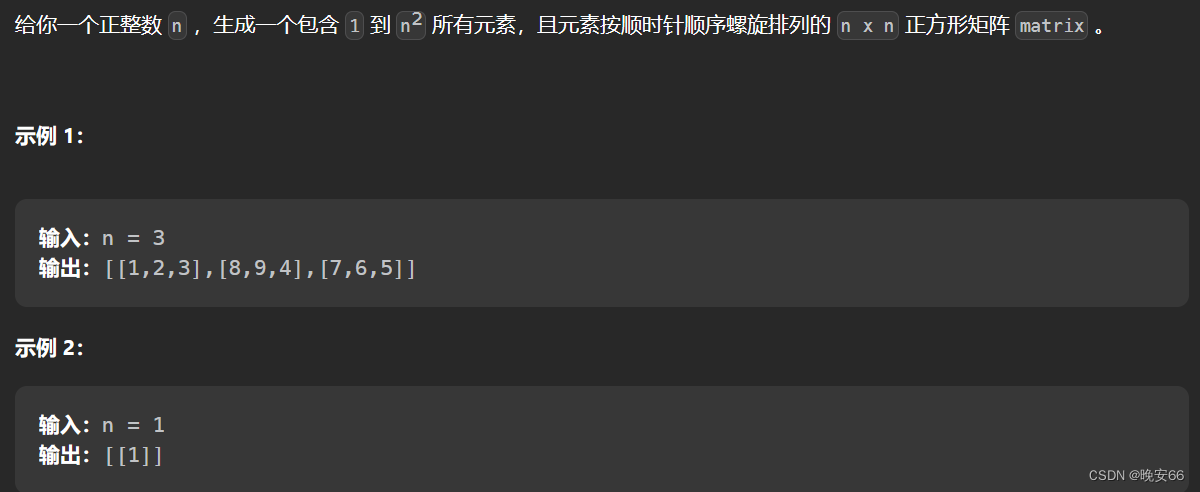
在这里插入图片描述

一、方向向量法

思路分析：螺旋矩阵在旋转过程中，我们选择的区间是左闭右开区间[ , ]，例如方向为从左往右赋值时，从(0,0)赋值到(0,n-1),然后调转方向，赋值(1,n-1)到(n-1,n-1) 。简单示意图如下：
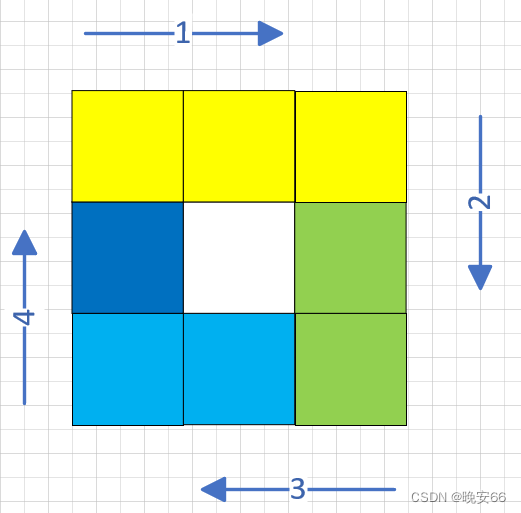
在这里插入图片描述

分析矩阵变换的增量delta_x和delta_y，这两个变量以右下左上的顺序变化时，其值依次为：{{0,1},{1,0},{0,-1},{-1,0}}。那么我们发现delta_x = delta_y, delta_y = - delta_x。那么我们再引入一个临时变量用来交换。然后就是程序边界问题，程序当中使用if语句，res下一个

程序如下：

class Solution {
public:
    // 方向向量法
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0));  // vector(n, ele)使用两次，就构造处一个嵌套vector矩阵
        int delta_x = 0, delta_y = 1;
        int x = 0, y = 0;
        for (int i = 1; i <= n * n; i++) {
            res[x][y] = i;
            if (res[(x + delta_x + n) % n][(y + delta_y + n) % n] != 0) { // 判断是否转弯，当dy为-1会造成 y+dy < 0，数组越界，加n是为了防止这个问题
                int tmp = delta_y;
                delta_y = -delta_x;
                delta_x = tmp;
            }
            x += delta_x;
            y += delta_y;
        }
        return res;
    }
};

复杂度分析：

时间复杂度： $O(n^2)$ ，遍历 $n^2$ 遍。
空间复杂度： $O (1)$ 。

完整代码

# include<iostream>
# include <vector>
using namespace std;

class Solution {
public:
    // 方向向量法
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0));  // vector(n, ele)使用两次，就构造处一个嵌套vector矩阵
        int delta_x = 0, delta_y = 1;
        int x = 0, y = 0;
        for (int i = 1; i <= n * n; i++) {
            res[x][y] = i;
            if (res[(x + delta_x + n) % n][(y + delta_y + n) % n] != 0) { // 判断是否转弯，当dy为-1会造成 y+dy < 0，数组越界，加n是为了防止这个问题
                int tmp = delta_y;
                delta_y = -delta_x;
                delta_x = tmp;
            }
            x += delta_x;
            y += delta_y;
        }
        return res;
    }
};

void my_print(vector<vector<int>>nums, int n, string str) {
	cout << str << endl;
	for (vector<vector<int>>::iterator it = nums.begin(); it < nums.end(); it++) {
		for (vector<int>::iterator vit = (*it).begin(); vit < (*it).end(); vit++) {
			cout << *vit << ' ';
		}	
		cout << endl;
	}
	cout << endl;
}

int main()
{
	int n = 3;
	Solution s1;
	vector<vector<int>>matrix = s1.generateMatrix(n);
	my_print(matrix, n, "生成的矩阵：");
	system("pause");
	return 0;
}