【数据结构与算法】线性表 01 链表

news2024/11/26 2:35:13

  • 一、线性表
    • 1.1 概念与特点
    • 1.2 线性表的存储结构
    • 1.3 常见操作
    • 1.4 应用场景
  • 二、链表
    • 2.1 链表简介
    • 2.2 单向链表（单链表）
      • 2.21 基本概念
      • 2.22 单链表基本操作
      • 2.23 C语言实现
    • 2.3 双向链表
    • 2.4 循环链表

一、线性表

线性表是一种最基本、最简单的数据结构，数据元素之间仅具有单一的前驱和后继关系，它提供了简单而强大的方法来处理和操作数据集合。

1.1 概念与特点

  1. 定义：线性表是由n（n≥0）个数据元素组成的有限序列，其中每个元素只有一个前驱和一个后继（除了第一个和最后一个元素）。
  2. 特点：
    • 线性结构：线性表中的元素之间存在线性关系，每个元素仅有一个直接前驱和一个直接后继。
    • 有序性：线性表中的元素按照其在序列中的位置依次排列，位置由线性表的首尾确定。
    • 可变性：线性表的长度可以动态地增加或减少。

逻辑结构

线性表的数据元素具有抽象（即不确定）的数据类型，在实际问题中，数据元素的抽象类
型将被具体的数据类型所取代。（常见整形和结构体）

1.2 线性表的存储结构

线性表的存储结构有两种常见的实现方式：顺序存储和链式存储。

（1）顺序存储结构：

顺序存储结构使用一段连续的内存空间来存储线性表中的元素。在内存中，线性表的元素按照其在序列中的位置依次存放。其中，首元素存放在起始地址，后续元素紧接着存放在连续的内存单元中。

  • 优点：
    • 随机访问：由于元素在内存中的连续存储，可以通过元素的下标快速直接访问元素。
    • 简单高效：存取元素的时间复杂度为O(1)，适用于频繁访问和随机访问元素的场景。
  • 缺点：
    • 大小固定：顺序存储结构需要预先分配一段连续的内存空间，导致大小固定，不易扩展。
    • 插入和删除操作效率低：在插入和删除元素时，需要移动其他元素的位置，导致效率较低。

（2）链式存储结构：

链式存储结构通过节点之间的指针连接来存储线性表中的元素。每个节点包含两部分信息：数据域用于存储元素值，指针域用于指向下一个节点的地址。

  • 优点：

    • 灵活扩展：链式存储结构可以动态地分配内存，便于根据实际需求进行大小的调整。
    • 插入和删除操作效率高：在插入和删除元素时，只需调整相邻节点的指针，效率较高。

  • 缺点：

    • 随机访问困难：由于元素之间不是连续存储的，无法通过下标直接访问元素，需要从头节点开始依次遍历至目标位置。
    • 需要额外的指针空间：链式存储结构需要额外的指针空间来存储节点之间的连接关系。

总结：

顺序存储结构适用于频繁访问和随机访问元素的场景，而链式存储结构适用于动态大小和频繁插入、删除操作的场景。

1.3 常见操作

  1. 插入操作：向线性表的指定位置插入一个新元素，需要移动后续元素的位置。
  2. 删除操作：从线性表中删除指定位置的元素，需要移动后续元素的位置。
  3. 查找操作：根据元素的值或位置在线性表中进行查找，可以获取指定元素或元素所在位置的信息。
  4. 修改操作：修改线性表中指定位置的元素的值。
  5. 获取长度：获取线性表中元素的个数。

1.4 应用场景

线性表作为一种基本的数据结构，广泛应用于各个领域，包括但不限于以下几个方面：

  1. 数组：数组是线性表的一种实现方式，用于存储具有相同类型的数据集合，广泛用于数据存储和处理、图像处理、数值计算等领域。
  2. 链表：链表是线性表的另一种实现方式，通过指针将元素连接起来，常用于动态内存管理、数据库系统、操作系统等领域。
  3. 栈：栈是一种特殊的线性表，遵循"先进后出"（LIFO）的原则，常用于函数调用、表达式求值、撤销操作等场景。
  4. 队列：队列是一种特殊的线性表，遵循"先进先出"（FIFO）的原则，常用于任务调度、消息传递、缓冲区管理等场景。

二、链表

2.1 链表简介

链表是一种常见且重要的数据结构，用于组织和存储数据。相比于顺序存储结构，链表通过节点之间的指针连接实现元素的存储和访问。本节将详细介绍链表的概念、特点、常见的类型以及操作和应用场景。

（1）概念与特点：

  1. 定义：链表是由一系列节点组成的数据结构，每个节点包含一个数据元素和一个指向下一个节点的指针。
  2. 特点：
    • 链式结构：链表中的节点通过指针相互连接，形成链式结构。
    • 无序性：链表中的节点可以按任意顺序排列。
    • 可变性：链表的长度可以动态地增加或减少，不需要预先分配固定大小的内存空间。

（2）常见类型：

  1. 单向链表：每个节点只包含一个指向下一个节点的指针，最后一个节点指向空值。
  2. 双向链表：每个节点同时包含指向前一个节点和后一个节点的指针，使得可以在链表中进行双向遍历。
  3. 循环链表：最后一个节点的指针指向头节点，形成一个闭环的链表结构。

（3）常见操作：

  1. 插入操作：在链表的指定位置插入一个新节点，需要调整相邻节点的指针。
  2. 删除操作：从链表中删除指定位置的节点，需要调整相邻节点的指针。
  3. 查找操作：根据节点的值或位置在链表中进行查找，可以获取指定节点或节点所在位置的信息。
  4. 修改操作：修改链表中指定节点的值。
  5. 获取长度：获取链表中节点的个数。

（4）应用场景：

链表作为一种灵活的数据结构，广泛应用于各个领域，特别适用于以下几个方面：

  1. 动态数据集合：由于链表的可变性，适用于需要频繁插入和删除操作的场景，如实时数据流处理、编辑器的撤销操作等。
  2. 内存管理：链表的灵活性使其成为动态内存分配的基础，用于管理堆内存中的空闲块或垃圾回收算法。
  3. 数据结构的实现：链表是许多其他高级数据结构的基础，如栈、队列和图等，提供了灵活性和效率的支持。

2.2 单向链表（单链表）

2.21 基本概念

单链表（singly linked list）是用一组任意的存储单元存放线性表的元素，这组存储单元可以连续也可以不连续，甚至可以零散分布在内存中的任意位置。

为了能正确表示元素之间的逻辑关系，每个存储单元在存储数据元素的同时，还必须存储其后继元素所在的地址信息，即指针，这两部分组成了数据元素的存储映像，称为结点（node）。
在这里插入图片描述

单链表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起的，由于每个结点只有一个指针域，故称为单链表。

单链表中每个结点的存储地址存放在其前驱结点的 指针域中，而第一个元素无前驱，所以设头指针（head pointer）指向第一个元素所在结点（称为开始结点），整个单链表的存取必须从头指针开始进行，因而头指针具有标识一个单链表的作用；由于最后一个元素无后继，故最后一个元素所在结点（称为终端结点）的指针域为空，即NULL（图中用“∧”表示），也称尾标志（tail mark）。

在这里插入图片描述

上面的表述中：元素从第一个节点开始存储，看起来没什么问题。但是当链表为空、在最前面插入和删除元素、遍历链表时会更加麻烦。所以，通常在第一个元素的节点前面添加一个头结点。（在后面的介绍中，可以想象没有头结点应该如何操作）

在这里插入图片描述

2.22 单链表基本操作

细介绍单链表的各种操作：

（1）创建链表：

创建一个空的单链表需要初始化一个头指针，并将头指针指向空值。

（2）插入操作：

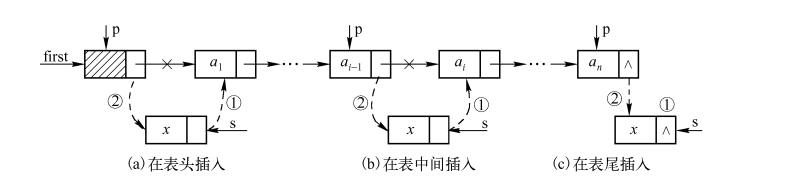
  • 头部插入：创建一个新节点，将新节点的指针指向原头节点，再将头指针指向新节点。
  • 尾部插入：遍历链表，找到最后一个节点，将最后一个节点的指针指向新节点，再将新节点的指针指向空值。
  • 中间插入：找到插入位置的前一个节点，将新节点的指针指向前一个节点的下一个节点，再将前一个节点的指针指向新节点。
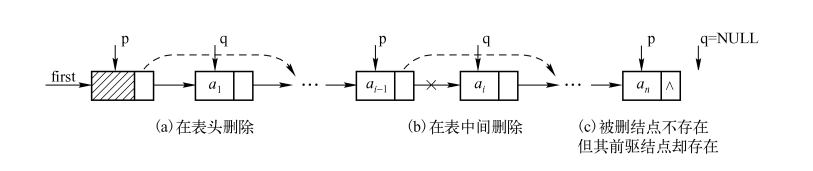
    在这里插入图片描述

（3）删除操作：

  • 删除头节点：将头指针指向头节点的下一个节点，并释放原头节点的内存。
  • 删除尾节点：遍历链表，找到倒数第二个节点，将该节点的指针指向空值，并释放最后一个节点的内存。
  • 删除指定位置的节点：找到要删除位置的前一个节点，将前一个节点的指针指向要删除节点的下一个节点，并释放要删除节点的内存。

在这里插入图片描述

（4）查找操作：

  • 根据值查找：从头节点开始遍历链表，比较每个节点的值与目标值，直到找到匹配的节点或遍历到链表末尾。
  • 根据位置查找：从头节点开始遍历链表，按照位置依次查找，直到找到目标位置的节点或遍历到链表末尾。

  1. 修改操作：
    根据指定位置或节点，将节点的数据域修改为新的值。

  2. 获取链表长度：
    从头节点开始遍历链表，累计节点的个数，直到遍历到链表末尾。

  3. 遍历链表：
    从头节点开始依次遍历每个节点，可以输出节点的值或进行其他操作。

需要注意的是，在进行插入和删除操作时，要确保链表的指针关系正确，避免出现内存泄漏或指针丢失的情况。

单链表的操作灵活性较高，尤其适用于频繁插入和删除操作的场景。然而，由于无法直接访问前一个节点，某些操作可能需要从头节点开始遍历整个链表，因此在使用时需注意操作的效率。

2.23 C语言实现

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点结构
typedef struct Node {
    int data;
    struct Node* next;
} Node;

// 创建一个新节点
Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode != NULL) {
        newNode->data = data;
        newNode->next = NULL;
    }
    return newNode;
}

// 在链表头部插入新节点
void insertAtHead(Node** head, int data) {
    Node* newNode = createNode(data);
    if (newNode != NULL) {
        newNode->next = *head;
        *head = newNode;
    }
}

// 在链表尾部插入新节点
void insertAtTail(Node** head, int data) {
    Node* newNode = createNode(data);
    if (newNode != NULL) {
        if (*head == NULL) {
            *head = newNode;
        } else {
            Node* current = *head;
            while (current->next != NULL) {
                current = current->next;
            }
            current->next = newNode;
        }
    }
}

// 在指定位置插入新节点
void insertAtPosition(Node** head, int data, int position) {
    if (position <= 0) {
        insertAtHead(head, data);
        return;
    }

    Node* newNode = createNode(data);
    if (newNode != NULL) {
        Node* current = *head;
        int currentPosition = 1;
        while (current != NULL && currentPosition < position) {
            current = current->next;
            currentPosition++;
        }
        if (current != NULL) {
            newNode->next = current->next;
            current->next = newNode;
        } else {
            free(newNode);  // 释放未使用的节点
            printf("Invalid position.\n");
        }
    }
}

// 删除头节点
void deleteAtHead(Node** head) {
    if (*head != NULL) {
        Node* temp = *head;
        *head = (*head)->next;
        free(temp);
    }
}

// 删除尾节点
void deleteAtTail(Node** head) {
    if (*head != NULL) {
        if ((*head)->next == NULL) {
            free(*head);
            *head = NULL;
        } else {
            Node* previous = *head;
            Node* current = (*head)->next;
            while (current->next != NULL) {
                previous = current;
                current = current->next;
            }
            previous->next = NULL;
            free(current);
        }
    }
}

// 删除指定位置的节点
void deleteAtPosition(Node** head, int position) {
    if (position <= 0) {
        deleteAtHead(head);
        return;
    }

    Node* current = *head;
    Node* previous = NULL;
    int currentPosition = 1;
    while (current != NULL && currentPosition < position) {
        previous = current;
        current = current->next;
        currentPosition++;
    }
    if (current != NULL) {
        if (previous != NULL) {
            previous->next = current->next;
        } else {
            *head = current->next;
        }
        free(current);
    } else {
        printf("Invalid position.\n");
    }
}

// 查找节点是否存在
int search(Node* head, int key) {
    Node* current = head;
    while (current != NULL) {
        if (current->data == key) {
            return 1;  // 节点存在
        }
        current = current->next;
    }
    return 0;  // 节点不存在
}

// 修改指定位置的节点值
void modify(Node* head, int position, int newData) {
    Node* current = head;
    int currentPosition = 1;
    while (current != NULL && currentPosition < position) {
        current = current->next;
        currentPosition++;
    }
    if (current != NULL) {
        current->data = newData;
    } else {
        printf("Invalid position.\n");
    }
}

// 获取链表长度
int getLength(Node* head) {
    int length = 0;
    Node* current = head;
    while (current != NULL) {
        length++;
        current = current->next;
    }
    return length;
}

// 遍历链表并打印节点值
void display(Node* head) {
    Node* current = head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

// 主函数测试链表操作
int main() {
    Node* head = NULL;

    insertAtHead(&head, 3);
    insertAtHead(&head, 2);
    insertAtHead(&head, 1);

    display(head);  // 输出：1 2 3

    insertAtTail(&head, 4);
    insertAtTail(&head, 5);

    display(head);  // 输出：1 2 3 4 5

    insertAtPosition(&head, 10, 3);

    display(head);  // 输出：1 2 10 3 4 5

    deleteAtHead(&head);

    display(head);  // 输出：2 10 3 4 5

    deleteAtTail(&head);

    display(head);  // 输出：2 10 3 4

    deleteAtPosition(&head, 2);

    display(head);  // 输出：2 3 4

    int key = 3;
    if (search(head, key)) {
        printf("%d exists in the list.\n", key);
    } else {
        printf("%d does not exist in the list.\n", key);
    }

    modify(head, 2, 8);

    display(head);  // 输出：2 8 4

    printf("Length of the list: %d\n", getLength(head));  // 输出：3

    return 0;
}

2.3 双向链表

吃宵夜去了，待续…

2.4 循环链表

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/621617.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Windows下安装及使用pip

Windows下安装及使用pip

首先查看Windows系统下是否安装有pip。终端执行下面命令&#xff1a; pip list # 查看Python中安装了哪些第三方库如果出现 ModuleNotFoundError: No module named ‘pip‘ 则说明系统里未安装成功pip。 那么可以先把pip安装上。安装pip可以选择 在线安装 或者 离线安装 两…
阅读更多...
网络配置心得-从switch网络加速出发

网络配置心得-从switch网络加速出发

背景&#xff1a; 在PC上玩战地5饱受外挂毒打&#xff0c;早想接触主机游戏又没有机会。最近突然有个好机遇带我入坑switch&#xff0c;那肯定得赶紧体验一下啊~~ 被安利的游戏是斯普拉遁3&#xff08;splatoon3&#xff09;&#xff0c;是一款switch独占的第三人称射击游戏&a…
阅读更多...
chatgpt赋能python：Python将yyyymmdd转换成yyyy-mm-dd的方法

chatgpt赋能python：Python将yyyymmdd转换成yyyy-mm-dd的方法

Python将yyyymmdd转换成yyyy-mm-dd的方法 Python语言不仅易于学习&#xff0c;而且是一种功能强大的语言&#xff0c;广泛应用于数据分析、人工智能和Web开发等领域。在实际开发过程中&#xff0c;我们经常遇到需要将日期格式转换为其他格式的需求。本文将介绍如何使用Python将…
阅读更多...
抖音账号矩阵系统|源码|开源代码独立部署难度

抖音账号矩阵系统|源码|开源代码独立部署难度

抖音账号矩阵系统&#xff0c;短视频账号矩阵系统源码&#xff0c; 短视频矩阵是一种常见的视频编码标准&#xff0c;它通过将视频分成多个小块并对每个小块进行压缩来实现高效的视频传输。在本文中&#xff0c;我们将介绍短视频矩阵的原理和实现&#xff0c;并提供示例代码。 …
阅读更多...
谈谈IPv6

谈谈IPv6

最近&#xff0c;在B站看到一个讲解IPv6背景的视频比较热门&#xff0c;而评论区则对IPv6技术有许多误解&#xff0c;这也反映出大家或许对这一新的协议不够了解&#xff0c;本文就谈谈我们生活中的IPv6。 另&#xff1a;前述的B站视频地址电子监听、全国断网&#xff0c;棱镜…
阅读更多...
Spring Boot 监听器详解

Spring Boot 监听器详解

Spring Boot 3.x系列文章 Spring Boot 2.7.8 中文参考指南(一)Spring Boot 2.7.8 中文参考指南(二)-WebSpring Boot 源码阅读初始化环境搭建Spring Boot 框架整体启动流程详解Spring Boot 系统初始化器详解Spring Boot 监听器详解 监听器的介绍 通过前面的几篇文章&#xff0c…
阅读更多...
基于三种机器学习模型的岩爆类型预测及Python实现

基于三种机器学习模型的岩爆类型预测及Python实现

写在前面 由于代码较多&#xff0c;本文仅展示部分关键代码&#xff0c;需要代码文件和数据可以留言 然而&#xff0c;由于当时注释不及时&#xff0c;且时间久远&#xff0c;有些细节笔者也记不清了&#xff0c;代码仅供参考 0 引言 岩爆是深部岩土工程施工过程中常见的一种地…
阅读更多...
GitHub创建新的项目

GitHub创建新的项目

想把最近自己做的一些东西整理一下上传到网上进行保存&#xff0c;然后就想到了Github&#xff0c;结果发现自己不会上传&#xff0c;所以去BiliBili大学学习了一下&#xff0c;一下内容主要参考《【程序员一定要掌握的技巧】使用Git上传本地代码到GitHub教程》。 使用Git上传本…
阅读更多...
Win10每次开机鼠标桌面右键都会显示撤销删除解决方法

Win10每次开机鼠标桌面右键都会显示撤销删除解决方法

Win10每次开机鼠标桌面右键都会显示撤销删除解决方法分享。有用户电脑开机的时候&#xff0c;就会自动弹出撤销删除的窗口了。那么这个问题是怎么回事呢&#xff1f;接下来我们就一起来看看以下的详细操作方法教学吧。 情况一&#xff1a; 如果是联想&#xff0c;在联想管家把联…
阅读更多...
Android 中的 NDK 到底是什么？（详细解析+案例实战）

Android 中的 NDK 到底是什么？（详细解析+案例实战）

NDK 提供了一系列的工具&#xff0c;帮助开发者快速开发 C (或 C )的动态库&#xff0c;并能自动将 so 和 java 应用一起打包成 apk&#xff1b;这些工具对开发者的帮助是巨大的 什么是 NDK &#xff1f; Android 原生开发包 NDK(Native Delopment kits )将用于 Android 平台上…
阅读更多...
Vue中process.env关键字，process.env.VUE_APP_BASE_API

Vue中process.env关键字，process.env.VUE_APP_BASE_API

1.process.env 是Node.js 中的一个环境 打开命令行查看环境&#xff1a; 2.process.env与Vue CLI 项目 Vue Cli 有以下三种运行模式 development 模式用于 vue-cli-service serve test 模式用于 vue-cli-service test:unit production 模式用于 vue-cli-service build 和 vue-c…
阅读更多...
pip安装教程 python（针对于Windows系统）

pip安装教程 python（针对于Windows系统）

1.什么是pip pip 是 Python 包管理工具&#xff0c;该工具提供了对Python 包的查找、下载、安装、卸载的功能。 目前如果你在 python.org 下载最新版本的安装包&#xff0c;则是已经自带了该工具。 pip 官网&#xff1a;https://pypi.org/project/pip/ 2.判断本机是否安装p…
阅读更多...
chatgpt赋能python：Python中如何将NaN变为0

chatgpt赋能python：Python中如何将NaN变为0

Python中如何将NaN变为0 Python是一种动态、强类型的编程语言&#xff0c;因其简单易学、功能强大&#xff0c;被广泛应用于各种领域。其中NumPy和Pandas是数据科学界最常用的Python库&#xff0c;而在数据处理中&#xff0c;处理缺失值通常是必不可少的。本文将介绍如何使用P…
阅读更多...
学成在线----day3

学成在线----day3

1、JSR303校验 对填入的数据自动做一些约束 package com.xuecheng.content.model.dto;import io.swagger.annotations.ApiModel; import io.swagger.annotations.ApiModelProperty; import lombok.Data;import javax.validation.constraints.NotEmpty; import javax.validati…
阅读更多...
PyCharm安装教程（2023年，3月）

PyCharm安装教程（2023年，3月）

下载PyCharm之前需要准备下载Python 链接&#xff1a;Python安装教程 一、PyCharm下载 1、进入JetBrains官网&#xff1a; 官网地址&#xff1a;https://www.jetbrains.com/ 2、点击【Developer Tools】 开发者工具&#xff0c;选择【PyCharm】点击跳转到PyCharm界面。点击…
阅读更多...
【Docker】 7.Docker Internet

【Docker】 7.Docker Internet

文章目录 Docker InternetDocker Internet CommandDocker Bridge Internetdocker Host InternetDocker Container InternetDocker None Internet Docker Internet Docker 网络架构采用的设计规范是CNM&#xff08;Container Network Model&#xff09;。CNM中规定了Docker网络…
阅读更多...
RK3588平台开发系列讲解（同步与互斥篇）自旋锁死锁实验

RK3588平台开发系列讲解（同步与互斥篇）自旋锁死锁实验

平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 一、自旋锁死锁二、实验程序的编写2.1、驱动程序编写2.2、编写测试 APP沉淀、分享、成长，让自己和他人都能有所收获！😄 📢自旋锁若是使用不当就会产生死锁，在本篇将会对自旋锁的特殊情况-死锁进行讲解。 一、自…
阅读更多...
0801详解-redux-react

0801详解-redux-react

文章目录 1 redux1.1 概述1.2 示例实现页面数字的加、减1.3 异步加-异步action 2 react-redux2.1 概述2.2 优化示例代码 3 数据共享4 redux开发者工具5 小结5.1 求和案例_redux精简版5.2 求和案例_redux完整版5.3 求和案例_redux异步action版5.4 求和案例_react-redux基本使用5…
阅读更多...
【哈士奇赠书活动 - 25期】-〖Python自动化办公应用大全（ChatGPT版） 〗

【哈士奇赠书活动 - 25期】-〖Python自动化办公应用大全（ChatGPT版） 〗

文章目录 ⭐️ 赠书 - 《Python自动化办公应用大全&#xff08;ChatGPT版&#xff09;》⭐️ 内容简介⭐️ 作者简介⭐️ 编辑推荐⭐️ 赠书活动 → 获奖名单 ⭐️ 赠书 - 《Python自动化办公应用大全&#xff08;ChatGPT版&#xff09;》 ⭐️ 内容简介 本书全面系统地介绍了P…
阅读更多...
使用YOLOv5实现图片、视频的目标检测

使用YOLOv5实现图片、视频的目标检测

推断的准备工作 接下来我将从官方代码开始&#xff0c;一步一步展示如何进行图片、视频识别 首先从GitHub下载官方代码&#xff08;也可以从下面链接获取&#xff09;&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/16wzV899D90TY2Xwhx4TwhA 提取码&#xff1a;vzvj …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023