3.3.1 绘制直方图 bar()

  直方图（Histogram）又称质量分布图，是统计报告图的一种，由一系列高度不等的纵向条纹或线段表示数据分布的情况，一般用横轴表示数据所属类别，纵轴表示数量或者占比。
  用直方图可以比较直观地看出产品质量特性的分布状态，便于判断其总体质量分布情况。直方图可以发现分布表无法发现的数据模式、样本的频率分布和总体的分布。
pyplot中绘制直方图的函数为bar()

matplotlib.pyplot.bar（left，height，width = 0.8，bottom = None，hold = None，data = None，** kwargs）

常用参数及说明如下表所示:

# 3.3 分析特征内部数据分布与分散状况
# 3.3.1 绘制直方图 bar()
# 1、绘制2017年第一季度各产业国民生产总值直方图
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load('F:/书籍/Python数据分析与应用/37304_Python数据分析与应用_源代码和实验数据/
第3章/data/国民经济核算季度数据.npz',allow_pickle=True)
name = data['columns']  # 提取其中的columns,作为数据的标签
# print("name:\n",name)
values = data['values']   # 提取其中的values数组，视为数据的存在位置
# print("values:\n", values)
label = ['第一产业', '第二产业','第三产业']  # 刻度标签
plt.figure(figsize = (6,5))  # 设置画布
# 绘制直方图
plt.bar(range(3), values[-1,3:6], width=0.5)  # values[-1,3:6] 最后一行的第3、4、5列
plt.xlabel('产业')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(3),label)# 添加x轴刻度
plt.title('2017年第一季度各产业国民生产总值直方图')
plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.2.2017年第一季度各产业国民生产总值直方图.png')
plt.show()

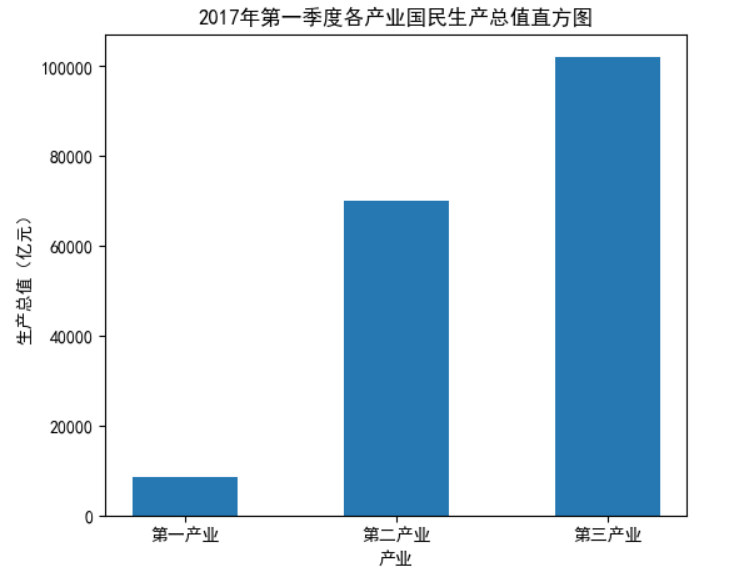
3.3.2 绘制饼图 pie()

  饼图（Pie Graph）是将各项的大小与各项总和的比例显示在一张“饼”中，以“饼”的大小来确定每一项的占比。
  饼图可以比较清楚地反映出部分与部分、部分与整体之间的比例关系，易于显示每组数据相对于总数的大小，而且显现方式直观。
pyplot中绘制饼图的函数为pie()

matplotlib.pyplot.pie(x, explode=None, labels=None, colors=None, autopct=None, pctdistance=0.6, shadow=False, labeldistance=1.1, startangle=None, radius=None, … )

常用参数及说明如下表所示:

plt.figure(figsize = (6,6))  # 设置画布为正方形，则绘制的饼图是正圆
label = ['第一产业', '第二产业','第三产业']  # 定义标签
ex = [0.01, 0.01, 0.01]  # 设定各项距离圆心n个半径

# 绘制饼图  # values[-1,3:6] 最后一行的第3、4、5列
plt.pie(values[-1,3:6], explode = ex, labels = label, autopct = '%1.1f%%')  

plt.title('2017年第一季度各产业国民生产总值饼图')
plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.2017年第一季度各产业国民生产总值饼图.png')
plt.show()

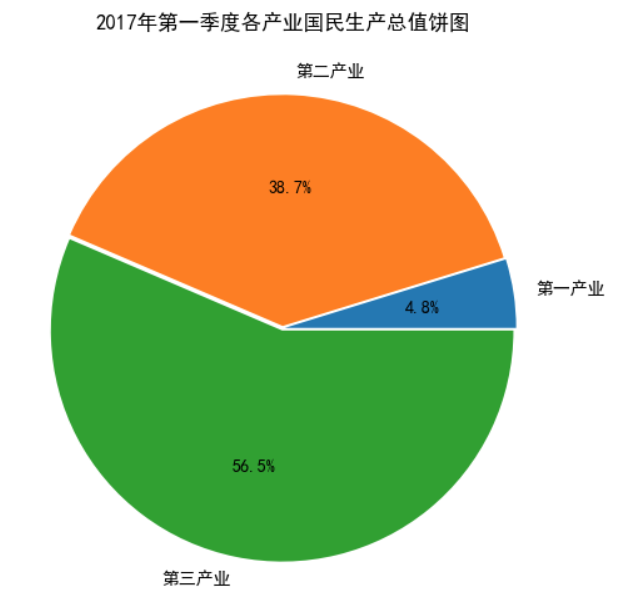
  可以明确看出3个产业在整个国民生产总值中的占比。第一产业不到5%，第三产业超过50%，说明我国经济的主要贡献为第三产业。

3.3.3 绘制箱线图 boxplot()

  箱线图（boxplot）也称箱须图，其绘制需使用常用的统计量，能提供有关数据位置和分散情况的关键信息，尤其在比较不同特征时，更可表现其分散程度差异。
  箱线图利用数据中的五个统计量（下边缘、下四分位数、中位数、上四分位数和上边缘）来描述数据，它也可以粗略地看出数据是否具有对称性、分布的分散程度等信息，特别可以用于对几个样本的比较。
pyplot中绘制箱线图的函数为boxplot(),其基本使用语法如下：

matplotlib.pyplot.boxplot(x, notch=None, sym=None, vert=None, whis=None, positions=None, widths=None, patch_artist=None,meanline=None, labels=None, … )

plt.figure(figsize = (6,4))  # 设置画布
label = ['第一产业', '第二产业','第三产业']  # 定义标签

# 绘制箱线图  # values[-1,3:6] 最后一行的第3、4、5列
gdp = (list(values[:,3]), list(values[:,4]), list(values[:,5]))
plt.boxplot(gdp, notch = True, labels = label, meanline = True)  

plt.title('2017年第一季度各产业国民生产总值箱线图')
plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.2017年第一季度各产业国民生产总值箱线图.png')
plt.show()

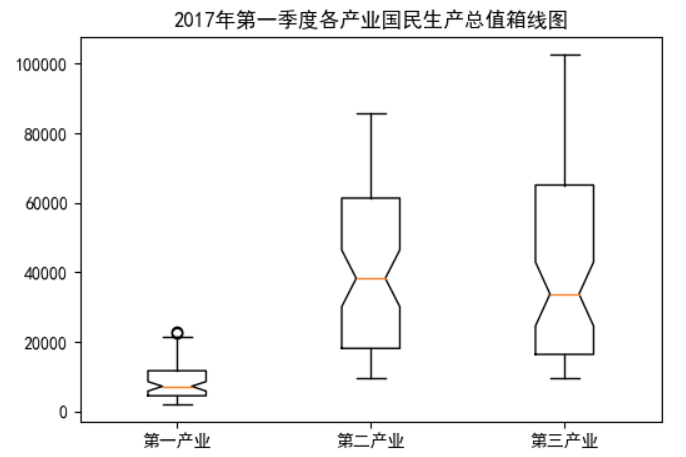
3.3.4 任务实现

1、绘制国民生产总值构成分布直方图

  通过直方图分析2000年第一季度和2017年第一季度的三大产业的国民生产总值,可以发现各产业绝对数值之间的关系，并通过对比发现产业结构的变化。同理可以得出行业间的绝对数值关系以及2000 ~2017年的行业发展状况。

# 1、绘制国民生产总值构成分布直方图
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load('F:/书籍/Python数据分析与应用/37304_Python数据分析与应用_源代码和实验数据/第3章/data/国民经济核算季度数据.npz',allow_pickle=True)
name = data['columns']  # 提取其中的columns,作为数据的标签
values = data['values']   # 提取其中的values数组，视为数据的存在位置
label1 = ['第一产业', '第二产业','第三产业']  # 刻度标签1
label2 = ['农业','工业', '建筑业', '批发', '交通', '餐饮', '金融', '房地产', '其他']  #刻度标签2

p = plt.figure(figsize = (12,12))
# 子图1
ax1 = p.add_subplot(2,2,1)
plt.bar(range(3), values[0,3:6], width=0.5)  # 绘制直方图
plt.xlabel('产业')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(3),label1)# 添加x轴刻度
plt.title('2000年第一季度国民生产总值产业构成分布直方图')
# 子图2
ax1 = p.add_subplot(2,2,2)
plt.bar(range(3), values[-1,3:6], width=0.5)  # values[-1,3:6] 最后一行的第3、4、5列
plt.xlabel('产业')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(3),label1)# 添加x轴刻度
plt.title('2017年第一季度国民生产总值产业构成分布直方图')

# 子图3
ax1 = p.add_subplot(2,2,3)
plt.bar(range(9), values[0,6:], width=0.5)  #  绘制直方图
plt.xlabel('行业')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(9),label2)# 添加x轴刻度
plt.title('2000年第一季度国民生产总值行业构成分布直方图')
# 子图4
ax1 = p.add_subplot(2,2,4)
plt.bar(range(9), values[-1,6:], width=0.5)  #  绘制直方图
plt.xlabel('行业')
plt.ylabel('生产总值（亿元）')
plt.xticks(range(9),label2)# 添加x轴刻度
plt.title('2017年第一季度国民生产总值行业构成分布直方图')

plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.绘制国民生产总值构成分布直方图.png')
plt.show()

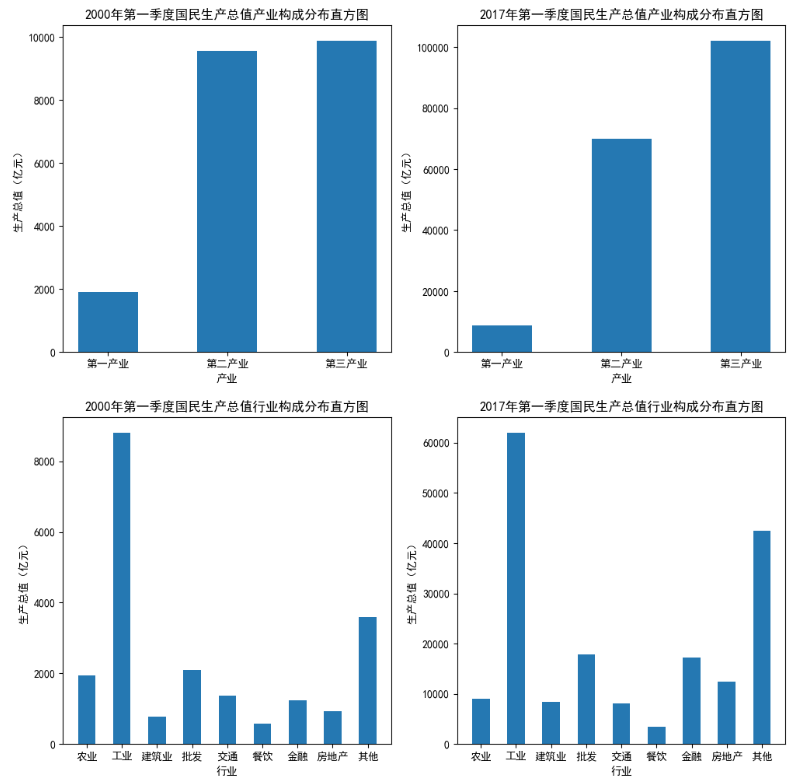
  可以看出,第一产业与第二产业和第三产业的国民生产总值差距愈发巨大。根据坐标轴变化可以发现，国民生产总值增长接近10倍。2000~2017年，金融行业与其他行业增长幅度相比较较明显。

2、绘制国民生产总值构成分布饼图

  通过分析2000年与2017年不同的产业和行业在国民生产总值中的占比，可以发现我国的产业结构变化和行业变迁。

# 绘制国民生产总值构成分布饼图
label1 = ['第一产业', '第二产业','第三产业']  # 刻度标签1
label2 = ['农业','工业', '建筑业', '批发', '交通', '餐饮', '金融', '房地产', '其他']  #刻度标签2
ex1 = [0.01, 0.01, 0.01]  # 设定各项距离圆心n个半径
ex2 = [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]  # 设定各项距离圆心n个半径
p = plt.figure(figsize = (11,11))
# 子图1
ax1 = p.add_subplot(2,2,1)
plt.pie(values[0,3:6], explode = ex1, labels = label1, autopct = '%1.1f%%') # 绘制饼图 
plt.title('2000年第一季度国民生产总值产业构成分布饼图')
# 子图2
ax1 = p.add_subplot(2,2,2)
plt.pie(values[-1,3:6], explode = ex1, labels = label1, autopct = '%1.1f%%') # 绘制饼图
plt.title('2017年第一季度国民生产总值产业构成分布饼图')
# 子图3
ax1 = p.add_subplot(2,2,3)
plt.pie(values[0,6:], explode = ex2, labels = label2, autopct = '%1.1f%%') # 绘制饼图
plt.title('2000年第一季度国民生产总值行业构成分布饼图')
# 子图4
ax1 = p.add_subplot(2,2,4)
plt.pie(values[-1,6:], explode = ex2, labels = label2, autopct = '%1.1f%%') # 绘制饼图
plt.title('2017年第一季度国民生产总值行业构成分布饼图')

plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.绘制国民生产总值构成分布饼图.png')
plt.show()

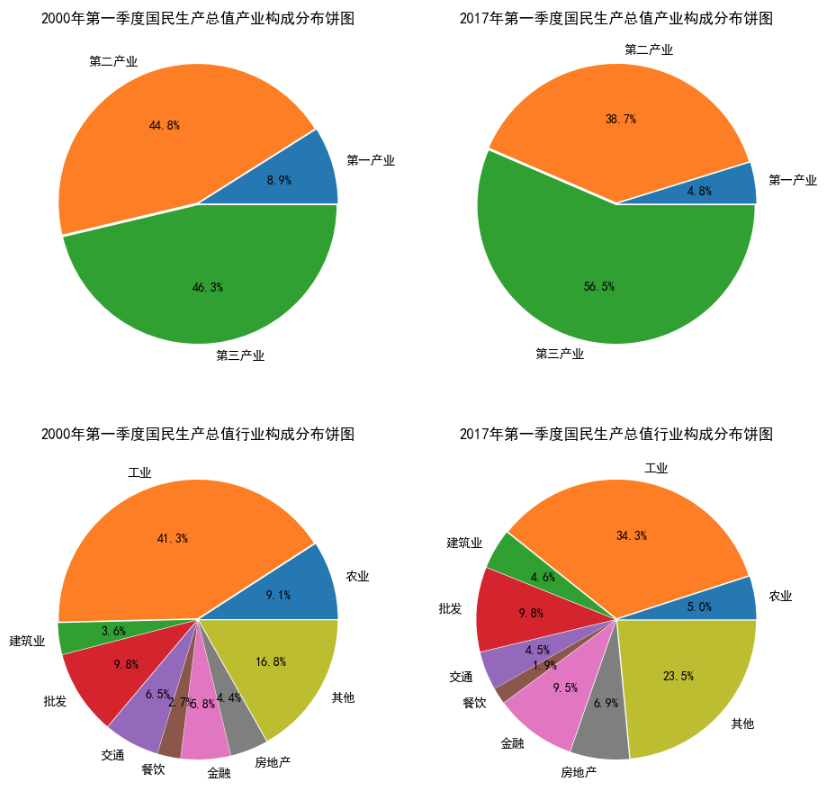
  可以看出,2000~2017年第三产业在整个国民生产总值中的占比约提高了10%，第一产业和第二产业在国民生产总值中的上比分别下降了约4%和6%。工业在整个国民生产总值中的比例下降了7%，其他行业与全融行业则分别提升了6.7%与3.7%。

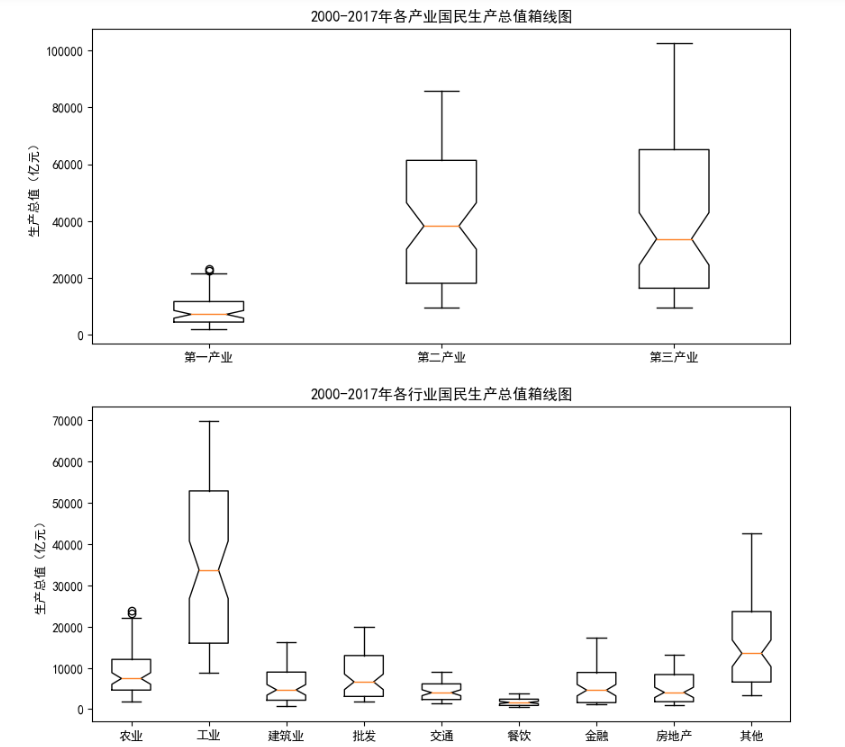
3、绘制国民生产总值分散情况箱线图

  通过箱线图分析2000 ~2017年不同的产业和行业在国民生产总值中的分散情况,从而判断整体增速是否加快。

# 3、绘制国民生产总值构成分布箱线
label1 = ['第一产业', '第二产业','第三产业']  # 刻度标签1
label2 = ['农业','工业', '建筑业', '批发', '交通', '餐饮', '金融', '房地产', '其他']  #刻度标签2
gdp1 = (list(values[:,3]), list(values[:,4]), list(values[:,5]))
gdp2 = ([list(values[:,i]) for i in range(6,15)])
p = plt.figure(figsize = (10,10))
# 子图1
ax1 = p.add_subplot(2,1,1)
plt.boxplot(gdp1, notch = True, labels = label1, meanline = True)  # 绘制箱线图
plt.title('2000-2017年各产业国民生产总值箱线图')
plt.ylabel('生产总值（亿元）')
# 子图2
ax1 = p.add_subplot(2,1,2)
plt.boxplot(gdp2, notch = True, labels = label2, meanline = True)  # 绘制箱线图
plt.title('2000-2017年各行业国民生产总值箱线图')
plt.ylabel('生产总值（亿元）')

plt.savefig('F:/书籍/Python数据分析与应用/自己实现/3.绘制国民生产总值构成分布箱线图.png')
plt.show()

小结

本章以2000至2017年各季度国民生产总值数据为例，介绍了pyplot绘图的基本语法，常用参数。
  介绍了分析特征间相关关系的散点图。
  分析特征间趋势关系的折线图。
  分析特征内部数据分布的直方图和饼状图。
  以及分析特征内部数据分散情况的箱线图。
为深入学习Matplotlib数据可视化打下了深厚的基础。