基数计数(cardinality counting) 通常用来统计一个集合中不重复的元素个数,例如统计某个网站的UV,或者用户搜索网站的关键词数量。数据分析、网络监控及数据库优化等领域都会涉及到基数计数的需求。
要实现基数计数,最简单的做法是记录集合中所有不重复的元素集合,当新来一个元素,若集合中不包含元素,则将加入,否则不加入,计数值就是的元素数量。这种做法存在两个问题:
- 当统计的数据量变大时,相应的存储内存也会线性增长
- 当集合变大,判断其是否包含新加入元素的成本变大
在redis 中,如果我们不需要获取数据集的内容,而只是想得到不同值的个数,那么就可以使用HyperLogLog( HLL)数据类型来优化使用集合类型时存在的内存和性能问题。
用法示例:
doitedu03:6379> PFADD HN:CS abc
(integer) 1
doitedu03:6379> PFADD HN:CS bbb
(integer) 1
doitedu03:6379> PFADD HN:CS ccc
(integer) 1
doitedu03:6379> PFADD HN:CS bbc
(integer) 1
doitedu03:6379> PFADD HN:CS bbc
(integer) 0
doitedu03:6379> PFCOUNT HN:CS
(integer) 4
doitedu03:6379> PFADD HN:ZZ bbb
(integer) 1
doitedu03:6379> PFADD HN:ZZ ccc
(integer) 1
doitedu03:6379> PFADD HN:ZZ ddd
(integer) 1
doitedu03:6379> PFADD HN:ZZ eee
(integer) 1
doitedu03:6379> PFCOUNT HN:ZZ
(integer) 4
doitedu03:6379> PFMERGE HN HN:ZZ HN:CS
OK
doitedu03:6379> PFCOUNT HN
(integer) 6
找规律:
给定N个随机得整数,从右往左数0得个数记录最大的K值,找K和N得关系。
hash算法转换成16位的二进制

| N(我一共去了几个数字) | log2N | K(最大的0的个数) |
|---|---|---|
| 3400 | 11.73 | 11 |
| 3500 | 11.77 | 12 |
| 4000 | 11.97 | 12 |
| 4100 | 12.00 | 14 |
| 9100 | 13.15 | 13 |
| 9200 | 13.17 | 16 |
| 9700 | 13.24 | 12 |
| 9800 | 13.26 | 15 |
| 9900 | 13.27 | 13 |
| 10000 | 13.29 | 13 |
结论:数学结论N ≈ 2^k N是我一共传进去多少个数 K 是最后我数出来0的个数
如果N介于(2k,2k+1),用这种方式估值计算的值都等于2^k,显然误差比较大,所以用加权的方式来降低误差。
加权公式:

redis中的Hyperloglog
redis使用16384个分桶来实现HLL结构,使标准误差达到0.8125%。
redis使用的散列函数具有64位输出,这意味着它使用前14位来寻找“桶”,剩下的50位用于计算右边的0的数量。正如我们之前看到的,每个存储子集将存储最大的“连0数”,最大可能为50(因为散列中只有50个剩余位可以是0),每个存储子集需要6位才能能够存储最多50个(二进制为110010)。因此我们得到98304个bit来存储1个HLL结构;如果我们将这些bit转换为byte,我们得到6*16384/8 = 12288个byte(或12kb)这就是hyperloglog在redis实现占用的空间大小。
算法原理
Hyperloglog(HLL)是从Loglog算法派生的概率算法,用于确定非常大的集合的基数,而不需要存储其所有值。
正如之前所说,常规集合或位图可能非常耗费资源。HLL使用固定大小的结构来解决这个问题,根据实际使用情况,它可以低于16kb。作为低资源需求的代价,基数测量是概率性的,意味着具有小于2%的误差。也就是说:
假设我们有一个1000000个ID的集合,
2%的错误意味着有可能在计算基数时错过1000000个唯一身份用户,为20000
然后,我们可以得到以下两种最坏情况(1000000-20000)= 980.000 || (1000000 + 20000)= 1020000
看起来误差有点多,实际中大多数情况下HLL实现的错误率低于1%。而且由于存在错误率,所以使用HLL表示在其应用场景该误差是可以接受的。
基本原理
HLL的严格数学论证在这里不作解释,通俗来说HLL是通过散列中左边连续0的数量来估计给定集合的基数,因为一个好的哈希算法可以确保我们每个可能的散列具有大致相同的出现概率和均匀分布。这允许HLL算法基于具有最左边0的流的散列来估计它已经“看到”的元素的量。例如,假设我有一个哈希函数,给定一个元素它返回数字0-15的二进制表示:

其中二进制共有4位,每位出现0的概率是1/2,所以如果连续出现四个0则元素个数至少有16个,那么我如果得到一个左边有k个0元素则至少有2(k)个元素。
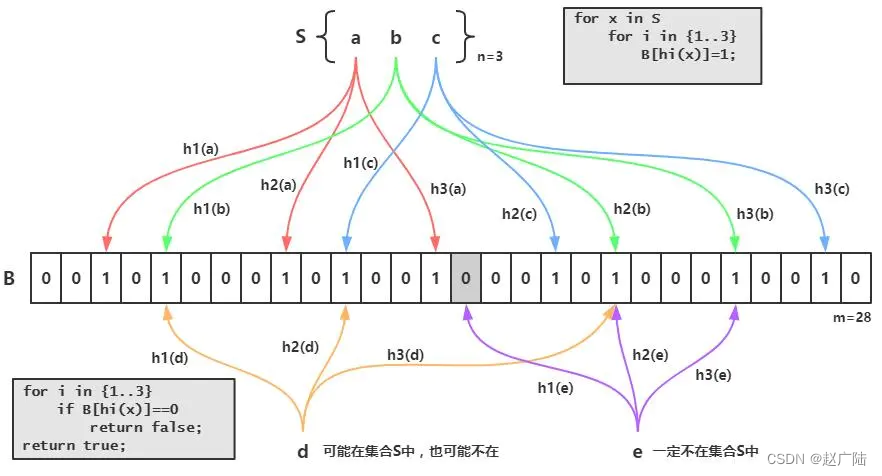
但是如果集合中只有一个元素,且元素每一位都是0怎么办,这时候就需要采用HLL中的分桶平均法了。分桶平均的基本原理是将统计数据划分为m个桶,每个桶分别统计各自的最大连续0个数并能得到各自的基数预估值 ,最终求其调和平均数即可,举个例子我们将集合划分为8个子集,那么需要将哈希值的前3位用于子集寻址,后几位从左边统计连续0的个数。
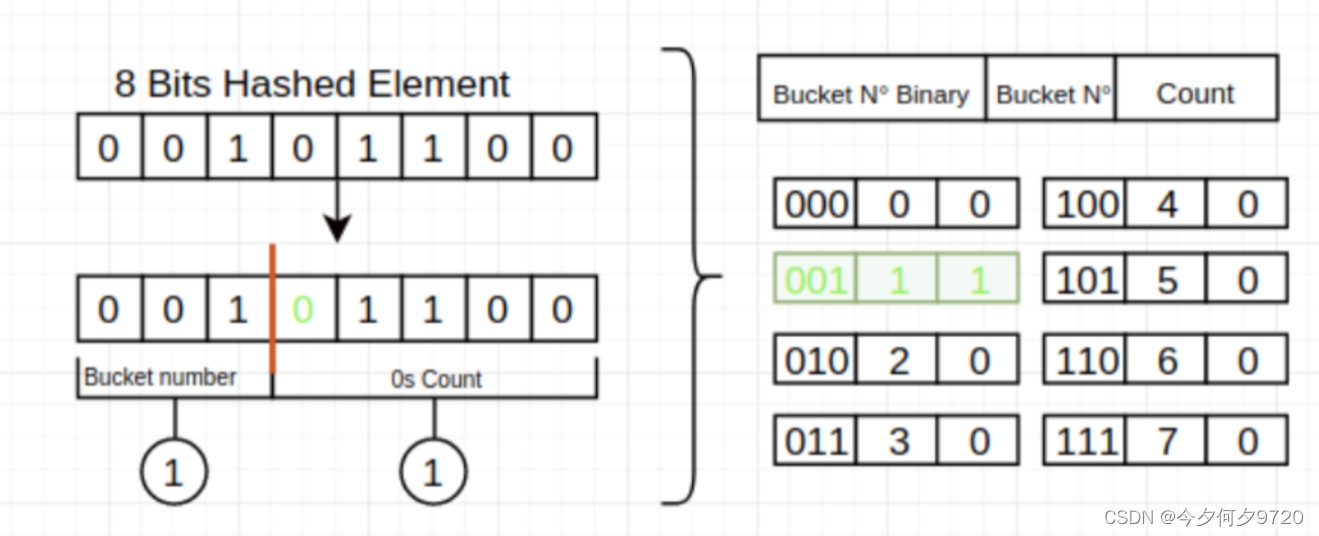
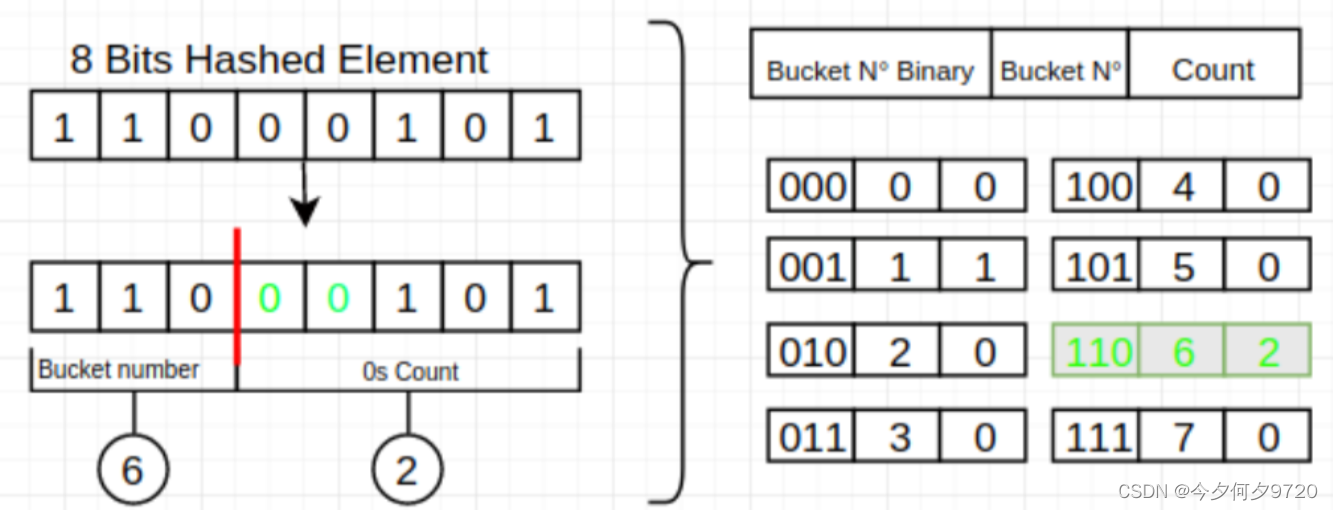
分段偏差修正
在HLLC的论文中,作者在实现建议部分还给出了在n相对于m较小或较大时的偏差修正方案。具体来说,设E为估计值:
当E <= 5m/2时,使用LC进行估计。
当 5m/2 < E <= 2(32)/30时,使用上面给出的HLC公式进行估计。
当 E > 2(32)/30时,估计公式如为
关于分段偏差修正效果分析也可以在算法原论文中找到。
严格的数学证明,需要用到伯努利分布,多重伯努利实验以及似然估计等数学知识;参考
https://www.cnblogs.com/linguanh/p/10460421.html
https://www.yuque.com/abser/aboutme/nfx0a4
https://zhuanlan.zhihu.com/p/77289303
https://zhuanlan.zhihu.com/p/26614750