本文分享一篇我们在IJCAI 2023的最新工作,文章分析了在离散时间事件序列上存在的瞬时效应问题,提出了一种利用瞬时效应的结构霍克斯模型,且在理论上证明了事件序列上的瞬时因果关系同样是可识别的。
相关论文:
Jie Qiao et al. “Structural Hawkes Processes for Learning Causal Structure from Discrete-Time Event Sequences” IJCAI 2023. arxiv.org: 2305.05986
介绍
现实中许多数据的都是以事件的形式记录的,例如系统日志,社交网络交互,购物行为,浏览行为等等都可以归结为一种事件序列,而在事件序列上学习事件类型之间的因果结构是一项重要且具有挑战的任务,也已经被广泛的应用,例如,在智能运维中的故障根因定位[1],在用户购物广告点击中的归因分析[2]等等。
现有方法,如基于多变量霍克斯过程的方法,大多都可以归结为学习所谓的格兰杰因果关系,其中隐含的假设是所有的事件都被即时且准确的记录,从而所有原因事件都严格地发生在其结果事件之前(也被称为(temporal precedence assumption))。
然而,由于有限的记录能力和存储容量,在许多现实世界应用中,以高精度记录事件的发生时间代价往往非常昂贵,我们通常只能访问相应的低精度离散时间事件序列。在这种低精度序列中,temporal precedence assumption将不再满足。
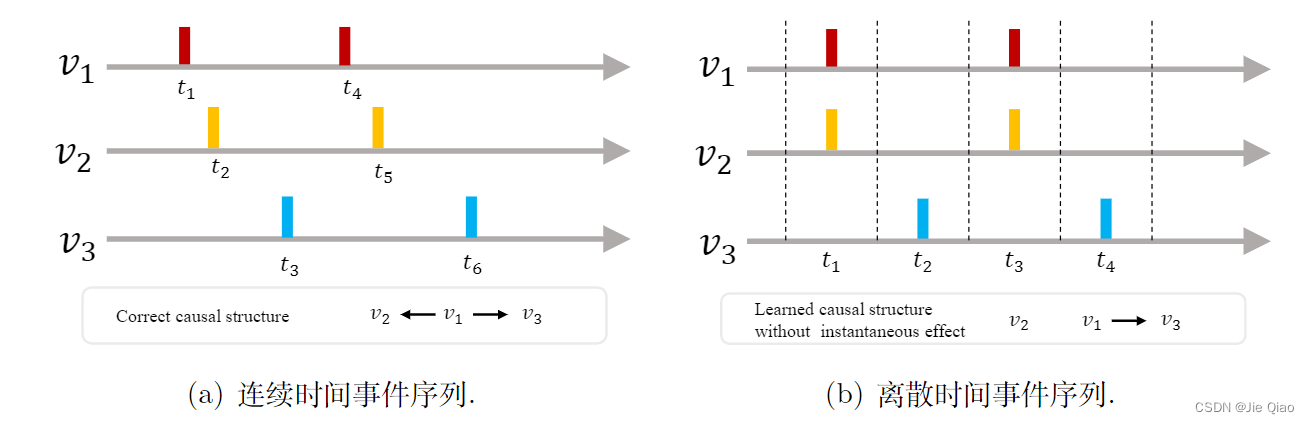
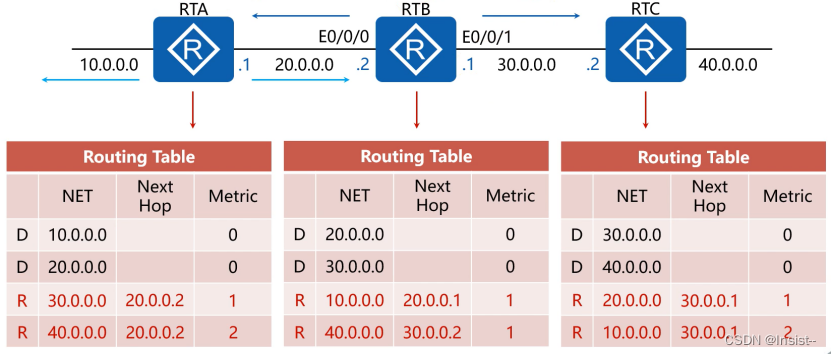
例如,图1中有三个事件类型,其产生的三个事件序列分别是 v 1 v_{1} v1, v 2 v_{2} v2, 和 v 3 v_{3} v3。设 v 1 v_{1} v1 是 v 2 v_{2} v2 和 v 3 v_{3} v3的原因,左图展示了高精度的事件序列,但现实中我们往往只能观测到右图中的离散时间事件序列。此时, v 1 v_{1} v1 和 v 2 v_{2} v2被视为了同时发生,违反了原因必须严格发生在其结果前的假设(temporal precedence assumption),使得现有基于格兰杰因果的方法无法识别该方向。因此,这篇论文旨在回答以下两个问题:
1)如何设计和学习一个利用离散时间中瞬时效应的霍克斯过程?
2)我们能否在瞬时效应存在的情况下识别事件序列中的因果关系?
结构霍克斯模型
针对第一个问题,我们提出了考虑在离散时间事件序列中利用瞬时效应的结构霍克斯过程(Structural Hawkes Processes, SHPs)。
为了建立瞬时效应的模型,我们首先将连续时间的计数过程扩展到观察事件序列的离散时间内或在 T = { Δ , 2 Δ , . . . , K Δ } \mathbf{T} =\{\Delta ,2\Delta ,...,K\Delta \} T={Δ,2Δ,...,KΔ}时刻收集数据, 其中 K = ⌊ T / Δ ⌋ K=\lfloor T/\Delta \rfloor K=⌊T/Δ⌋ , Δ > 0 \Delta >0 Δ>0 是每个观察时间的时间间隔长度。 那么离散时间的多变量计数过程可以定义为 N ( Δ ) = { N v ( Δ ) ( k ) ∣ k ∈ { 0 , … , K } , v ∈ V } \mathbf{N}^{(\Delta )} =\{N_{v}^{(\Delta )} (k)|k\in \{0,\dotsc ,K\},v\in \mathbf{V} \} N(Δ)={Nv(Δ)(k)∣k∈{0,…,K},v∈V},其中 N v ( Δ ) ( k ) = N v ( ( 0 , k Δ ] ) N_{v}^{(\Delta )} (k)=N_{v} ((0,k\Delta ]) Nv(Δ)(k)=Nv((0,kΔ]) 衡量不晚于 k Δ k\Delta kΔ发生的事件数量。我们进一步让 X = { X v , t ∣ v ∈ V , t ∈ { 0 , … , K } ] } \mathbf{X} =\{X_{v,t} |v\in \mathbf{V} ,t\in \{0,\dotsc ,K\}]\} X={Xv,t∣v∈V,t∈{0,…,K}]} 表示每个时间间隔内的观察值集合,其中 X v , t : = N v ( t Δ ) − N v ( ( t − 1 ) Δ ) X_{v,t} :=N_{v} (t\Delta )-N_{v} ((t-1)\Delta ) Xv,t:=Nv(tΔ)−Nv((t−1)Δ) 表示成 d N v ( t ) dN_{v} (t) dNv(t).
结构霍克斯过程的设计如下:
定义(结构霍克斯过程):
结构霍克斯过程是一个结构计数过程,即对所有
v
∈
V
v\in \mathbf{V}
v∈V,
N
v
(
Δ
)
N_{v}^{(\Delta )}
Nv(Δ)的强度可以写成:
λ
v
(
k
Δ
)
=
μ
v
+
∑
v
′
∈
V
∑
i
=
1
k
ϕ
v
′
,
v
(
(
k
−
i
)
Δ
)
X
v
,
i
,
(1)
\lambda _{v} (k\Delta )=\mu _{v} +\sum _{v'\in \mathbf{V}}\sum _{i=1}^{k} \phi _{v',v} ((k-i)\Delta )X_{v,i} ,\tag{1}
λv(kΔ)=μv+v′∈V∑i=1∑kϕv′,v((k−i)Δ)Xv,i,(1)
其中
ϕ
v
,
v
(
0
)
≡
0
\phi _{v,v} (0)\equiv 0
ϕv,v(0)≡0 保证在时间
k
Δ
k\Delta
kΔ上排除
v
v
v类型的事件
可以看到公式1中当前时间的强度不仅受到过去 ( k − 1 ) Δ (k-1)\Delta (k−1)Δ时间发生的事件的影响,也受同一时期 k Δ k\Delta kΔ发生的事件影响。基于该模型,我们可以结合[^1]中的方法给出了一种结合Minorize-Maximization算法以及爬山算法的因果结构学习算法。
可识别性
该文章的另一个问题是,我们能否在瞬时效应存在的情况下识别事件序列中的因果关系?
为了回答这个问题,我们建立的结构霍克斯过程与整数自回归INAR( ∞ \infty ∞)的联系:
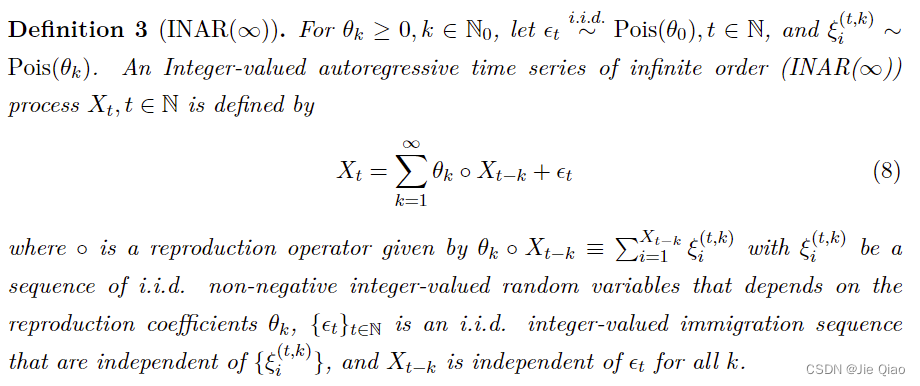
我们发现该模型与霍克斯过程具有内在一致性,基于此,我们可以通过上述模型来证明结构霍克斯过程的理论性质:

定理2说明了在二元瞬时因果关系中,该因果方向是可识别的,同时该结论也可以被推广到多变量的因果结构学习中:

实验
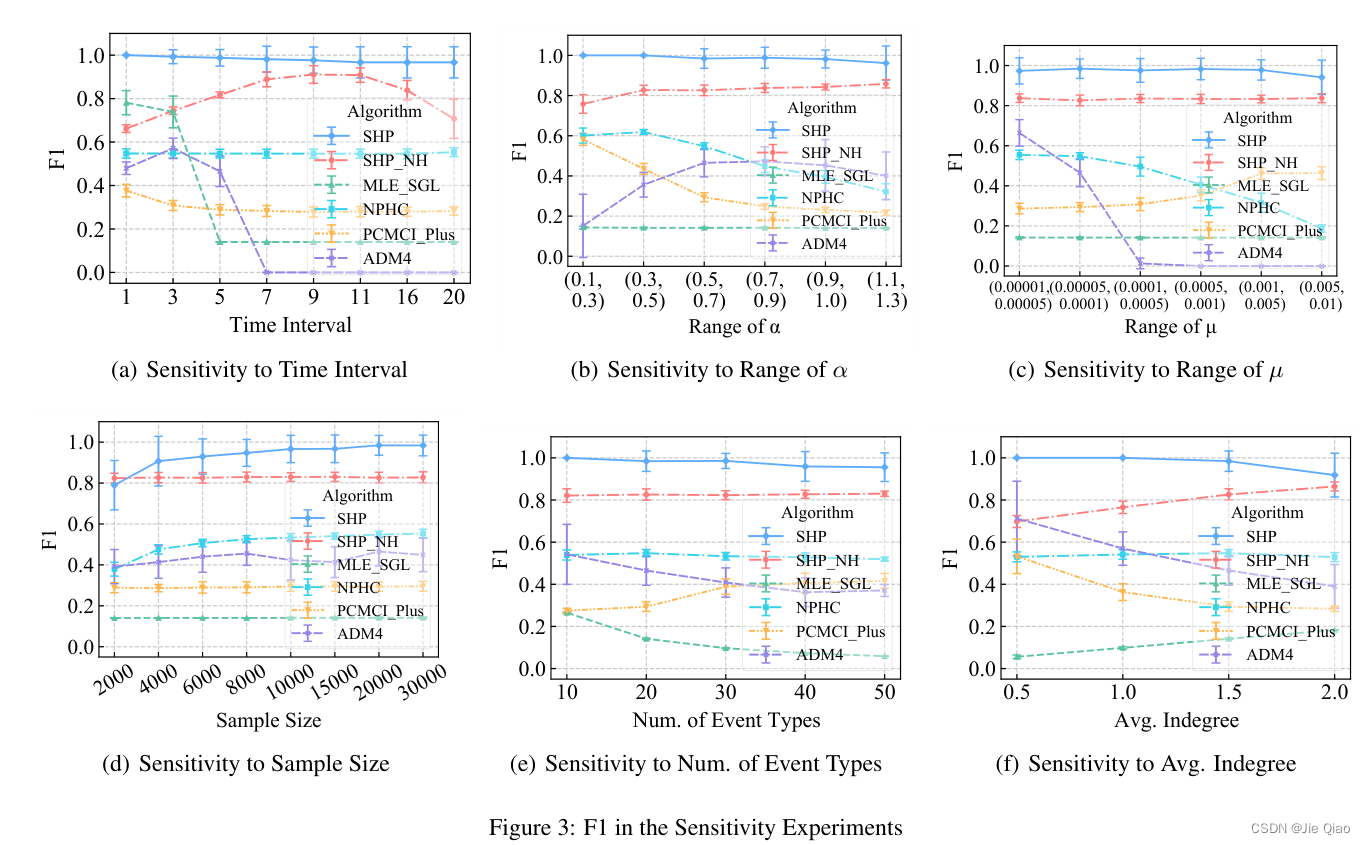
在实验中,在生成数据与真实数据分别进行了验证。在生成数据中,我们的结果均优于现有的方法:
在真实数据中,我们使用了[3]华为基站告警数据的真实数据集,其实验结果均优于现有的算法:
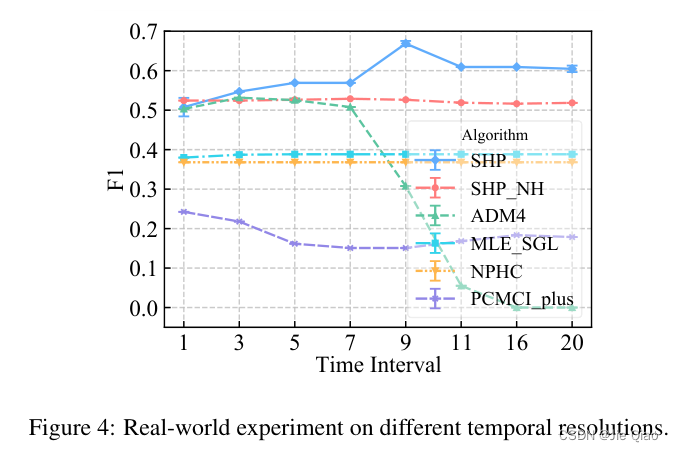
实验在不同的时间粒度上进行,有趣的是,我们把序列的粒度变得更粗反而会有助于提升效果,我们猜测原因是真实记录中存在时间不同步的情况,而粗粒度数据中形成的瞬时因果关系反而有助于因果发现。
结论
在这项工作中,我们研究了如何建模和利用瞬时效应来学习离散时间事件序列的因果结构。我们提出了利用瞬时效应的结构霍克斯过程和学习事件类型间因果结构的实用算法。理论结果表明,结构霍克斯过程中的瞬时因果结构确实是可以识别的。就我们所知,这是第一个针对具有瞬时效应的事件序列的因果结构学习方法。SHP的成功不仅为从现实世界的事件序列中学习因果结构提供了一个有效的解决方案,而且也为从离散时间事件序列中发现因果关系展示了一个有潜力的方向。
参考文献
[1]: Cai, R., Wu, S., Qiao, J., Hao, Z., Zhang, K., & Zhang, X. (2022). THPs: Topological Hawkes Processes for Learning Causal Structure on Event Sequences. IEEE Transactions on Neural Networks and Learning Systems.
[2]: J. Tao, Q. Chen, J. W. Snyder Jr, A. S. Kumar, A. Meisami, and L. Xue, “A Graphical Point Process Framework for Understanding Removal Effects in Multi-Touch Attribution,” arXiv preprint arXiv:2302.06075, 2023.
[3]: https://competition.huaweicloud.com/informations/mobile/1000041487/dataset