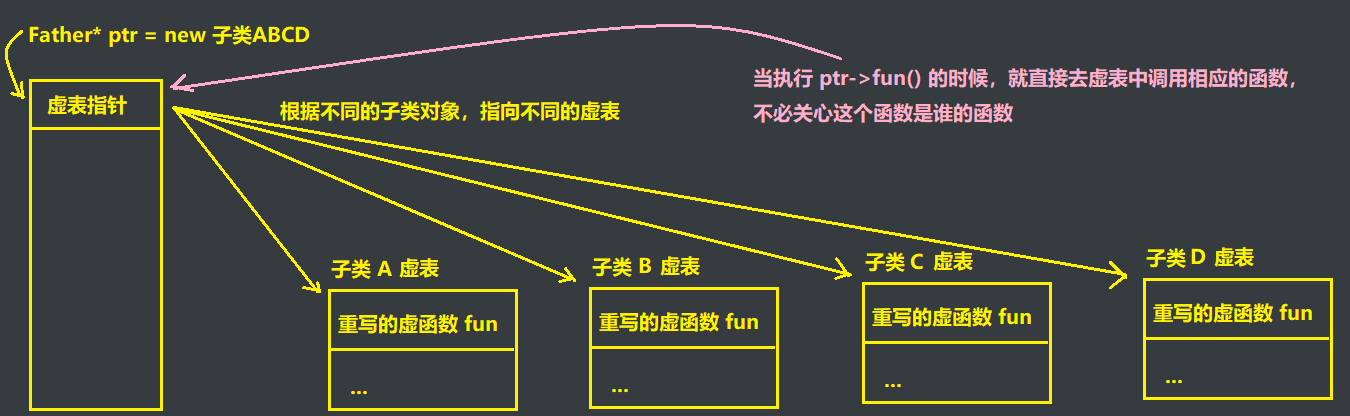
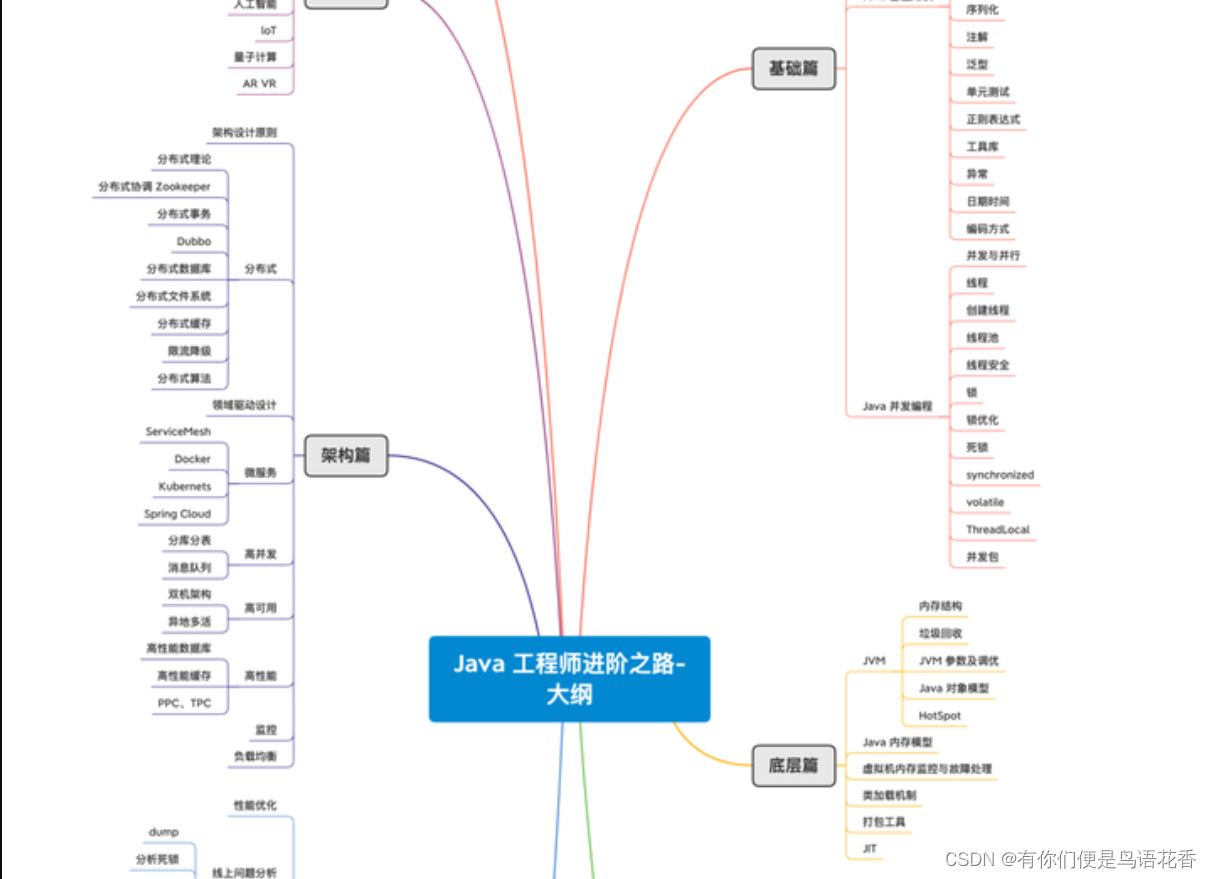
概览
时间复杂度与空间复杂度的作用是在衡量一个算法的优劣性,以及在二者之间进行权衡,寻找二者的平衡点。
时间复杂度是指执行算法所需时间的增长率,而空间复杂度则是指执行算法所需存储空间的增长率。
高时间复杂度的算法可能需要在短时间内完成大规模数据的计算,而高空间复杂度的算法可能需要占用大量的内存空间。
在进行算法设计和分析时,通常需要在时间和空间之间进行权衡,以找到适合特定问题的最佳算法。了解算法的时间和空间复杂度可以帮助我们确定在处理不同问题时哪些算法是可行的,以及如何优化算法以减少其时间和空间的占用。
- 数据结构和算法解决是 “如何让计算机时间更快、空间更省的方式解决问题”。
- 因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。
- 分别用时间复杂度(算法执行时间)和空间复杂度(占用空间)两个概念来描述性能问题,二者统称为复杂度。
- 复杂度描述的是算法执行时间(或占用空间)与数据规模的增长关系。
一、时间复杂度
算法的时间复杂度,也就是算法的时间量度。
时间复杂度表示算法运行时间的相对大小,是算法运行时间的增长率。特指在解决问题的规模(问题大小)趋于无穷大时,算法的运行时间与规模的关系。
它通常与输入数据进行比较,时间复杂度不是指具体的时间,而是算法的运算次数,是相对于问题规模的相对量。
举例:
当规模增长10倍时,算法的运行时间也增长了10倍,则该算法的时间复杂度为O(1)。如果规模增长10倍时,算法的运行时间增长了100倍,则该算法的时间复杂度为O(10)。
时间复杂度表示方法 - 大 O 表示法
算法的执行时间与每行代码的执行次数成正比,用 T(n) = O(f(n)) 表示,
T(n) :算法执行总时间,
f(n) :每行代码执行总次数
n: 数据的规模
实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势。
所以常量、低阶、系数实际上对这种增长趋势不产生决定性影响,我们在做时间复杂度分析时忽略这些项。
我们再看几个例子。
假设我们有一段代码
public static void main(String[] args) {
int i = 10;
for (int j = 0; j < i; j++) {
System.out.println("j" + j);
}
}
当运行这段代码时,所有语句的执行都需要花费时间,我们假设每条语句的执行时间一样,我们将代码进行拆解,如下
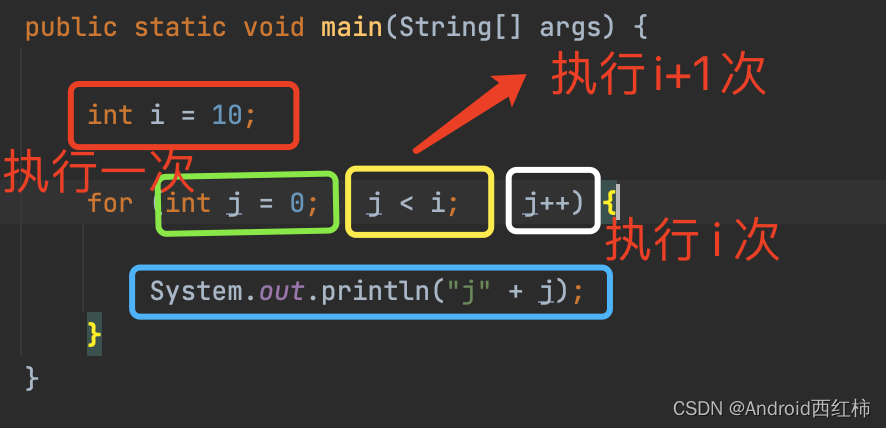
我们将这些次数加起来,总执行次数就 = 3 * i + 3; 当i 趋向于无穷大时, 我们可以忽略常数、低阶项、及高阶系数,这样总执行次数就 = i
T(i) = O(i)
时间复杂度计算
- 得出运行时间的函数
- 对函数进行简化,只保留最高阶项 (忽略常数、低阶项、及高阶系数等)
下面我们分别来举例说明
常数阶
时间复杂度为 T(n) = O(1)
function aFun() {
console.log("Hello, World!"); // 需要执行 1 次
return 0; // 需要执行 1 次
}
我们看到总共要执行2次,我们来简化一下,用1取代所有的常量,就变成了O(1)
时间复杂度为 T(n) = O(n)
function bFun(n) {
for(let i = 0; i < n; i++) { // 需要执行 (n + 1) 次
console.log("Hello, World!"); // 需要执行 n 次
}
return 0; // 需要执行 1 次
}
总共需要执行 3n + 2次,简化一下,O(n)
时间复杂度为 T(n) = O(n^2)
function cal(n) {
let sum = 0; // 1 次
let i = 1; // 1 次
let j = 1; // 1 次
for (; i <= n; ++i) { // n 次
j = 1; // n 次
for (; j <= n; ++j) { // n * n ,也即是 n平方次
sum = sum + i * j; // n * n ,也即是 n平方次
}
}
}
时间复杂度为 T(n) = O(log2n)
let i=1;
while (i <= n) {
i = i * 2;
}
代码是从 1 开始,每次循环就乘以 2,当大于 n 时,循环结束。
其实就是高中学过的等比数列,i 的取值就是一个等比数列。在数学里面是这样子的:
20 21 22 ... 2k ... 2x = n
所以,我们只要知道 x 值是多少,就知道这行代码执行的次数了,通过 2x = n 求解 x,
数学中求解得 x = log2n 。所以上面代码的时间复杂度为 O(log2n)。
二、空间复杂度
空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系
定义:算法的空间复杂度通过计算算法所需的存储空间实现,是对一个算法在运行过程中临时占用存储空间大小的量度
算法的空间复杂度的计算公式记作:S(n) = O(f(n)),
空间复杂度计算
public static void main(String[] args) {
int i = 10;
for (int j = 0; j < i; j++) {
System.out.println("j" + j);
}
}
随着i的变化,所需开辟的内存空间并不会随着i的变化而变化,因为 这 i、j 用的时相同的空间, i 、j各一个,简化一下就是 O(1)
n :问题的规模,
f(n) :语句关于 n 所占存储空间的函数。
function print(n) {
const newArr = []; // 第 2 行
newArr.length = n; // 第 3 行
for (let i = 0; i <n; ++i) {
newArr[i] = i * i;
}
for (let j = n-1; j >= 0; --j) {
console.log(newArr[i]) 当消耗空间和输入参数n保持线性增长
}
}
第 2 行代码中,申请了一个空间存储变量 newArr ,是个空数组。
第 3 行把 newArr 的长度修改为 n 的长度的数组,每项的值为 undefined ,
除此之外,剩下的代码都没有占用更多的空间,所以整段代码的空间复杂度就是 O(n)
我们常见的空间复杂度就是 O(1)、O(n)、O(n^2)






![设计模式-02.经典设计原则-第二节[必读]](https://img-blog.csdnimg.cn/990319dc459a4bdfa710d1bde387f84d.png)