二叉树OJ题详解

第一题：单值二叉树力扣链接：力扣

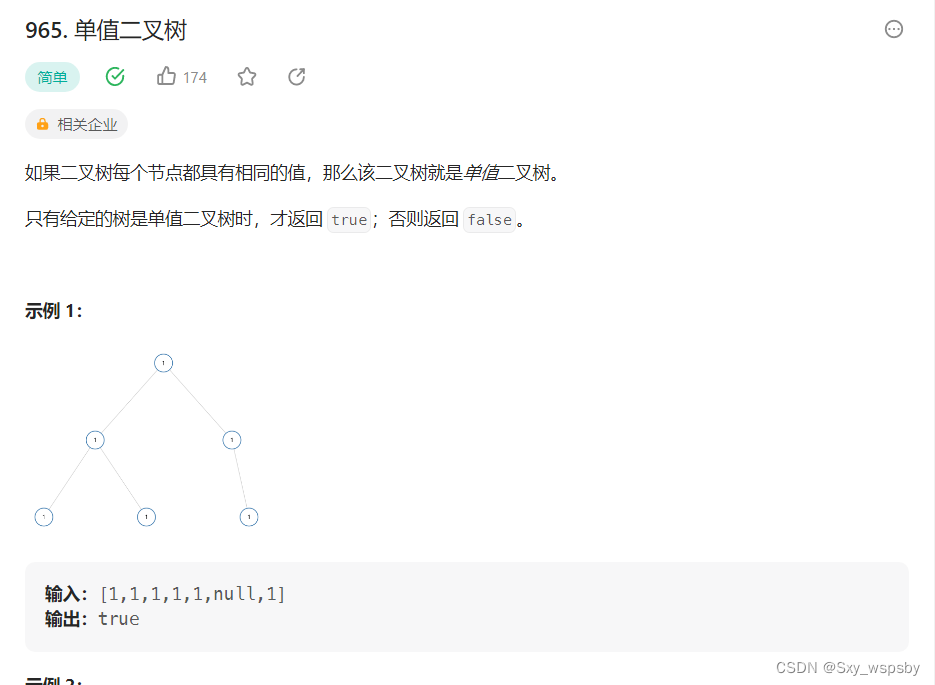
单值二叉树就是每一个节点存放的数据都相同，那么如何判断一棵树为单值二叉树呢？我们就拿最简单的一棵树为例子，比如根节点为1它的左子树和右子树也为1的一棵树，我们只需要比较根节点和它的左子树是否相等，根节点和它的右子树是否相等，也就是说判断一个二叉树是否为单值二叉树最重要的是判断父节点与左右子树的值是否相同。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isUnivalTree(struct TreeNode* root){
    if (root==NULL)
    {
        return true;
    }
    if (root->left&&root->val!=root->left->val)
    {
        return false;
    }
    if (root->right&&root->val!=root->right->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

如代码我们可以看到首先判断这棵树是否为空，我们要知道一颗空数也是单值二叉树，所以当这棵树为空就返回true，然后去判断这个节点的左子树是否存在，如果存在就让这个节点与它的左子树相比，如果不等于就说明不是单值二叉树，当我们在判断一棵树是否是什么样的树的时候我们大部分都要去找反例。判断完左子树再去判断右子树，当两个if语句都没有返回时就去递归这棵树的左子树和右子树直到程序结束。

第二题：二叉树最大深度力扣链接：力扣

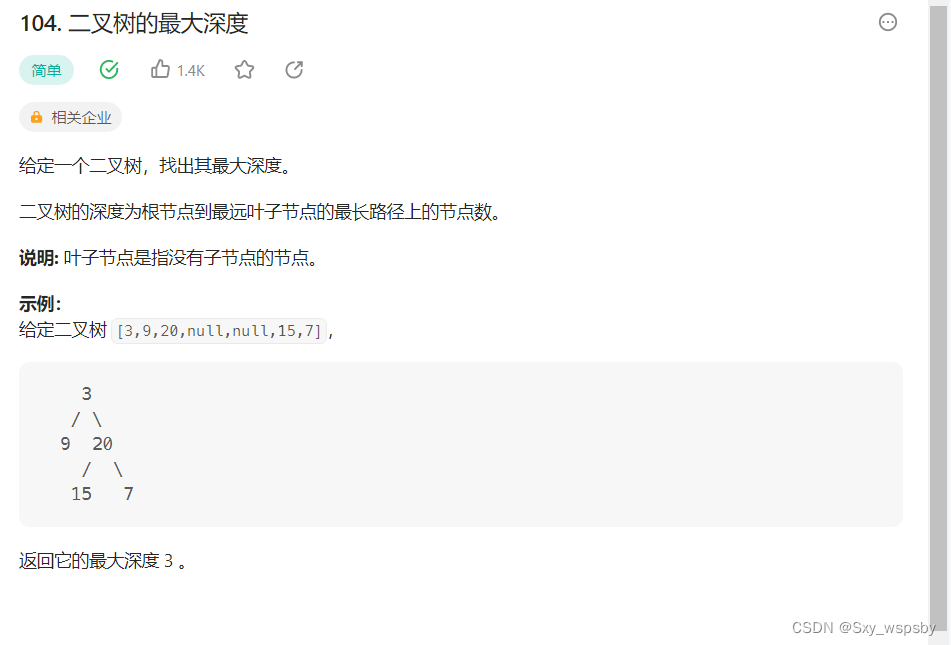
二叉树的最大深度相信我们并不陌生，我们在二叉树的构建中就讲解了二叉树的层数或者高度，这道题的本质就是求二叉树的高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


int maxDepth(struct TreeNode* root){
     if (root==NULL)
     {
         return 0;
     }
     int leftheight = maxDepth(root->left);
     int rightheight = maxDepth(root->right);
     return leftheight>rightheight?leftheight+1:rightheight+1;
}

我们只需要注意，当这棵树为空，那么层数就为0。用两个变量去记录这棵树的左子树的高度和右子树的高度，我们只需要返回左右子树中最大的那个，当两个数相等时任意返回一个即可。所以我们在返回的时候用了三目操作符，当左子树高度大于右子树高度时，我们就返回左子树高度再加上根节点的那一层高度即可。

第三题：相同的树力扣链接：力扣

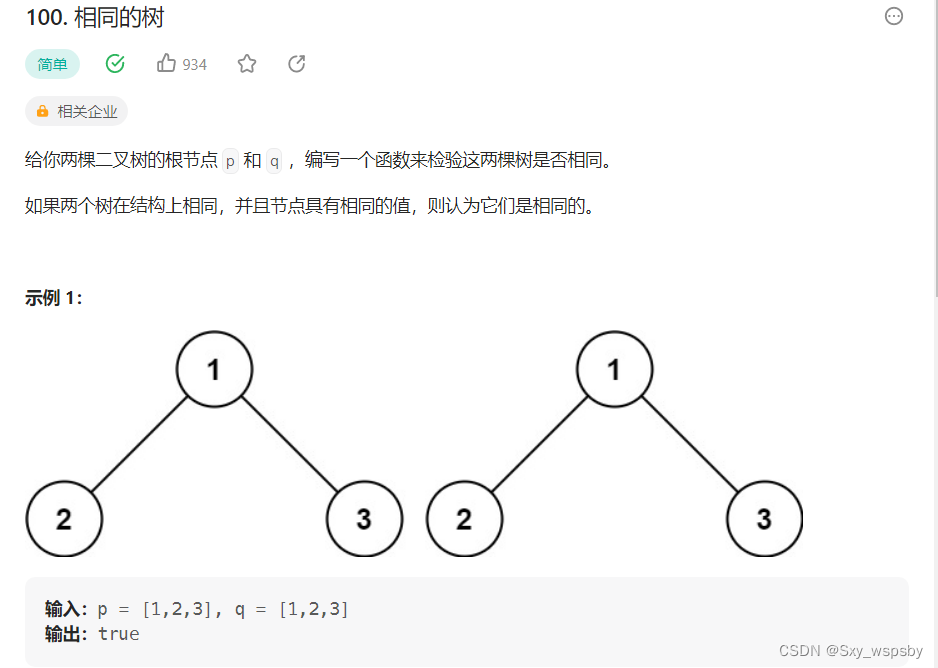
怎么判断两棵树是否相同呢？其实很简单，只需要看着两棵树的节点是否相同并且节点的左右子树也都是相同的，从这个角度出发，那么当两个树都为空树的时候那么这两棵树一定是相同的，当一棵树为空一棵树不为空那么这两棵树一定不相同，然后再去递归这个节点的左子树和另一棵树的左子树是否相同同时右子树也必须相同。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool isSameTree(struct TreeNode* p, struct TreeNode* q){
       if (p==NULL&&q==NULL)
       {
           return true;
       }
       if (p==NULL||q==NULL)
       {
           return false;
       }
       if (p->val!=q->val)
       {
           return false;
       }
       return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

代码中的P 和 Q 就是两颗不同的树，当两棵树都为空时那么就返回true，当一棵树为空一棵树不为空的时候就返回false，当第一棵树的节点和第二棵树的节点不相同的时候就返回false，然后再去递归第一棵树的左子树和第二棵树的左子树是否相等并且第一棵树的右子树也要和第二棵树的右子树相等。

第四题：二叉树的前序遍历力扣链接：力扣

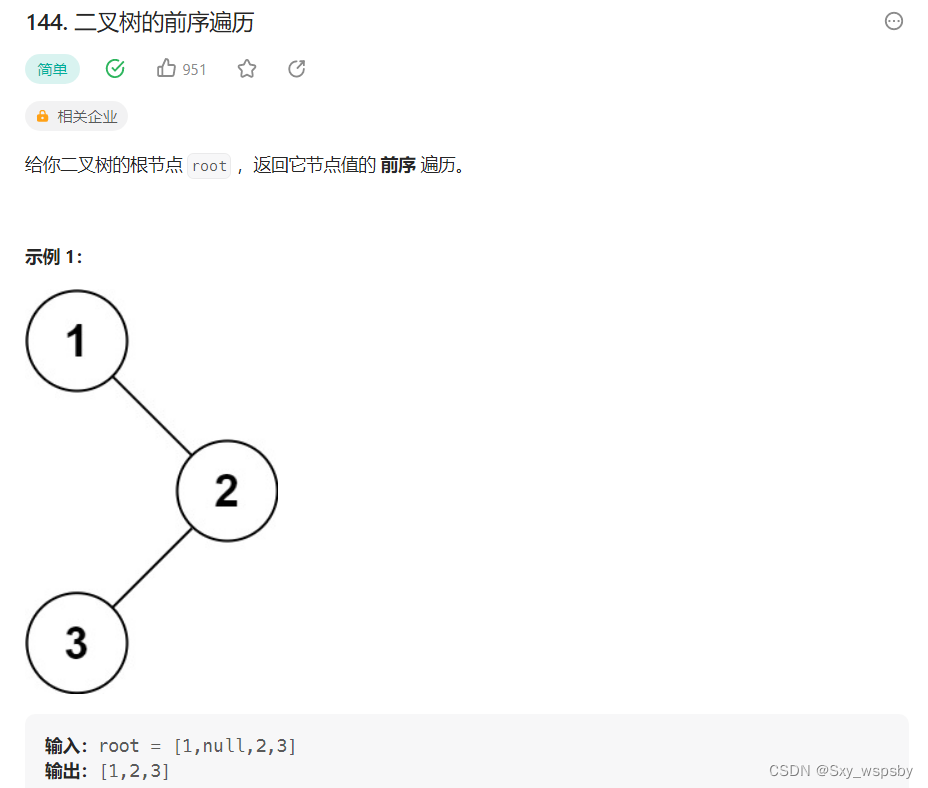
二叉树的前序遍历相信我们都并不陌生，但是这道题却有很多的坑，首先这道题并没有告诉我们数组的大小，也就是说我们要将遍历的数据放在数组中，但是每一个测试用例的数据多少都不一样，那么我们如何根据每一个测试用例有多少个节点就开辟多大的空间去存放数据呢？答案很简单，那就是先去计算这颗二叉树有多少个节点，然后直接给数组开辟这么大的空间即可。同样我们在往数组放数据的时候还需要一个下标，因为我们是用递归遍历的，所以这个下标一定要传地址过去。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int TreeSize(struct TreeNode* root)
{
    if (root==NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}
void PrevOrder(struct TreeNode* root,int* a,int* i)
{
     if (root==NULL)
     {
         return;
     }
     a[(*i)++]=root->val;
     PrevOrder(root->left,a,i);
     PrevOrder(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
      *returnSize = TreeSize(root);
      int*a = (struct TreeNode*)malloc(sizeof(int)*(*returnSize));
      int i = 0;
      PrevOrder(root,a,&i);
      return a;
}

如代码所示，我们必须将此题划分三个函数，有人问全放在一个函数实现不行吗？答案是不可以，我们在计算节点大小和前序遍历都用的是递归，了解递归的本质就知道这是不可能实现的。计算二叉树的节点我们已经讲过，当节点为空就返回0，否则就返回这个节点的左子树的节点加上右子树的节点然后再加上自己，然后我们利用这个函数的返回值来给数组a开辟空间，空间开好后我们定义一个变量去记录下标，将这个树的根和数组和下标的地址都传给前序遍历函数，当有节点为空我们就return一下，否则就将值放到数组里，我们既然传的是地址所以需要先解应用再++，然后去递归这个节点的左子树，在这里可能会有人问为什么递归的函数里传的是i而不是地址呢？我们要明白递归是自己调用自己，自己本来一开始就接收的是地址，所以在递归函数中i就是第一次传来的地址，如果将i改成&i则相当于拿第一次传来的地址的地址，如果这样就要用二级指针，三级指针一直往后累加了，所以切记在递归中要明白传值的意义。当前序遍历完成后数组里已经放完了数据这时候直接返回a数组即可。

第五题：翻转二叉树力扣链接：力扣

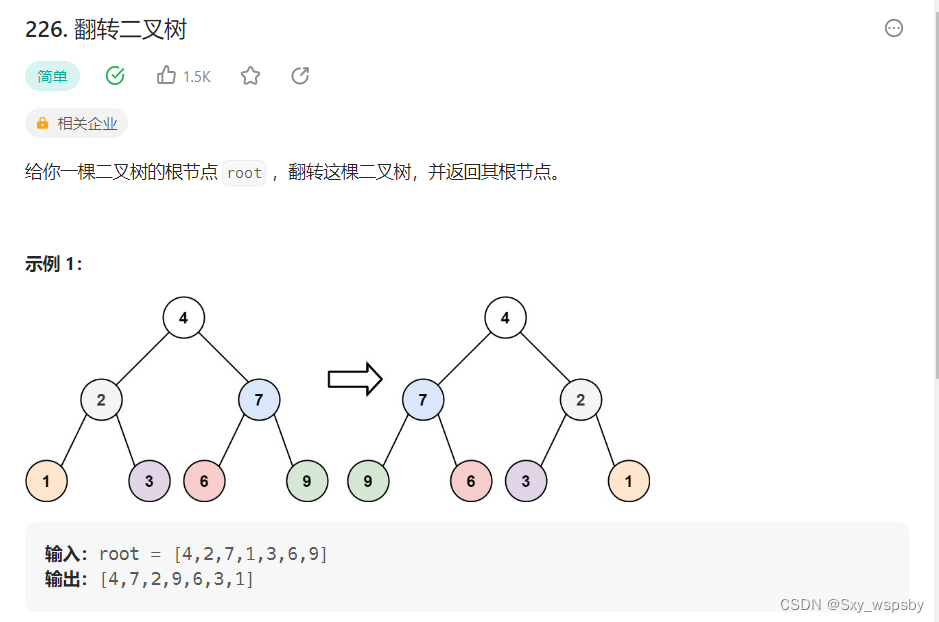
什么是翻转二叉树呢？其实就是将一颗二叉树的左子树和右子树交换，然后这个左子树的左子树与这个左子树的右子树再交换，这样一看就是递归了，方法也很简单，每次都是保存左子树的节点的地址然后将右子树给左子树，然后再将保存的左子树给右子树，然后再递归到这个节点的左子树右子树。明白了这个我们看代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

void Reverse(struct TreeNode* root)
{
    if (root==NULL)
    {
        return;
    }
    struct TreeNode*tmp = root->left;
    root->left = root->right;
    root->right = tmp;
    Reverse(root->left);
    Reverse(root->right);
}
struct TreeNode* invertTree(struct TreeNode* root){
     if (root==NULL)
     {
         return NULL;
     }
     Reverse(root);
     return root;
}

首先我们先判断这棵树是否为空树，如果是空树的话直接返回空指针即可，如果不是就去翻转，进入翻转函数后我们用变量保存这棵树的左子树，然后将右子树给左子树然后把保存的左子树给右子树，在这里我们不要判断这棵树的左子树和右子树是否为空，因为为空也不影响交换并且还有一边为空一边不为空的情况，所以我们直接去递归它的左子树和右子树，在递归的过程中如果遇到空节点那么就return一下。全部翻转后返回这棵树即可。

第六题：对称二叉树力扣链接：力扣

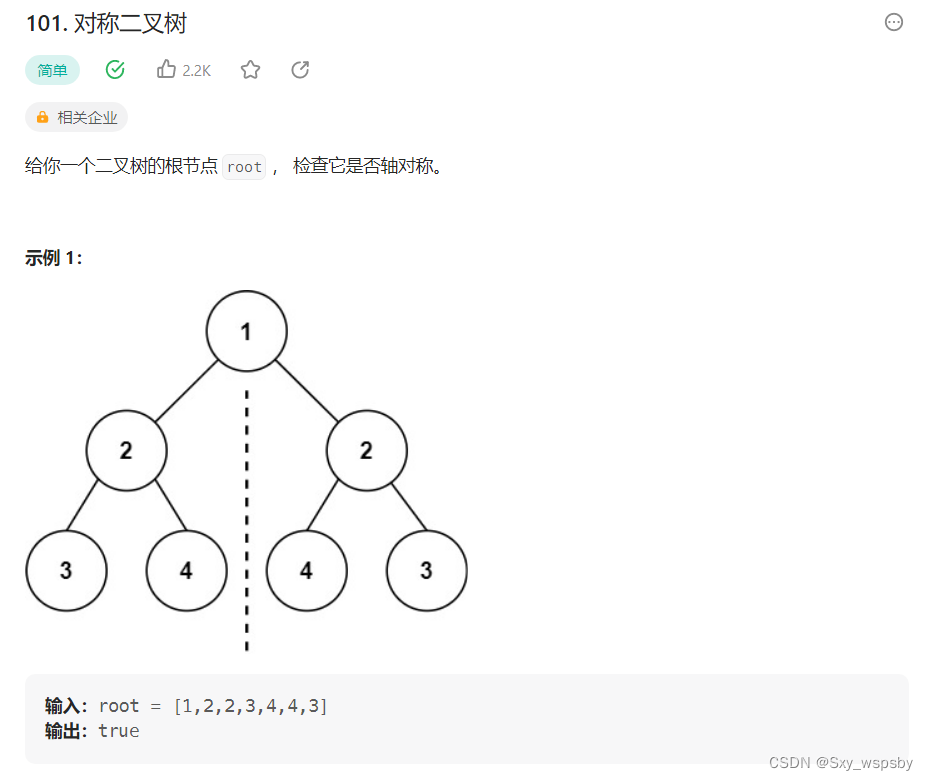
大家看到这道题有没有感觉到很熟悉呢？我们可以发现要判断一棵树是否对称，只需要判断这棵树的左子树的左子树是否等于这棵树的右子树的右子树，意思就是上图中左边2节点的左子树3要与右边2节点的右子树3相等。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2)
{
   if (root1==NULL&&root2==NULL)
   {
       return true;
   }
   if (root1==NULL||root2==NULL)
   {
       return false;
   }
   if (root1->val!=root2->val)
   {
       return false;
   }
   return _isSymmetric(root1->left,root2->right)&&_isSymmetric(root1->right,root2->left);
}

bool isSymmetric(struct TreeNode* root){
    return !root||_isSymmetric(root->left,root->right);
}

我们在判断前需要先判断这棵树是否为空，如果为空则也是对称的然后去判断这棵树的左子树和右子树是否满足条件，当左子树为空并且右子树为空那么一定是对称的，当只有一边的树不为空那么一定是不对称的，当左节点不等于右节点也是不对称的。然后去递归这棵树的左子树的左子树与这棵树的右子树的右子树是否对称满足条件并且这棵树的左子树的右子树也要和这棵树的右子树的左子树满足条件。

第七题：另一棵树的子树力扣链接：力扣

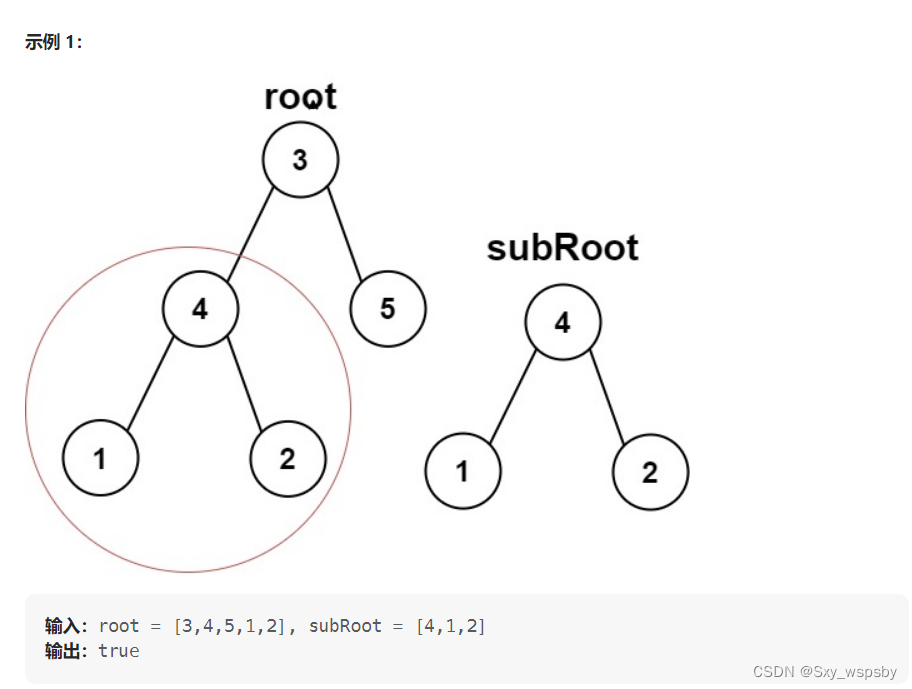
在做了前面几道判断对称或者相同数的题后看这道题就非常简单了，其实就是在第一个树中找到与第二个数相同的节点结构。我们只需要在第一棵树中递归，当发现第一棵树中的子树与第二棵树相同，那么就返回true。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSumTree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if (root==NULL&&subRoot==NULL)
    {
        return true;
    }
    if (root==NULL||subRoot==NULL)
    {
        return false;
    }
    if (root->val!=subRoot->val)
    {
        return false;
    }
    return isSumTree(root->left,subRoot->left)&&isSumTree(root->right,subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
     if (root==NULL)
     {
         return false;
     }
     if (isSumTree(root,subRoot))
     {
         return true;
     }
     return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

我们先判断第一棵树是否为空，如果第一棵树为空则一定不包含第二棵树。这里为什么不判断第二棵树为空呢？因为题目中告诉了第二棵树一定不为空。我们要写一个函数判断两棵树是否相同，当这个函数为真那么就返回true，否则就去递归第一棵树的左子树与第二棵树是否相等或者第一棵树的右子树与第二棵树是否相等。判断两棵树是否相同我们已经讲过，这道题只需要注意当在第一棵树的左子树发现了与第二棵树相同的数的时候直接返回true就不在递归第一棵树的右子树了，只有在第一棵树的左子树没有找到与第二棵树相同的数才需要去递归第一棵树的右子树。如果在第一棵树的左子树和右子树中都没有找到与第二棵树相同的树，那么就返回了false。

第八题：二叉树的构建及遍历牛客网链接：二叉树遍历_牛客题霸_牛客网

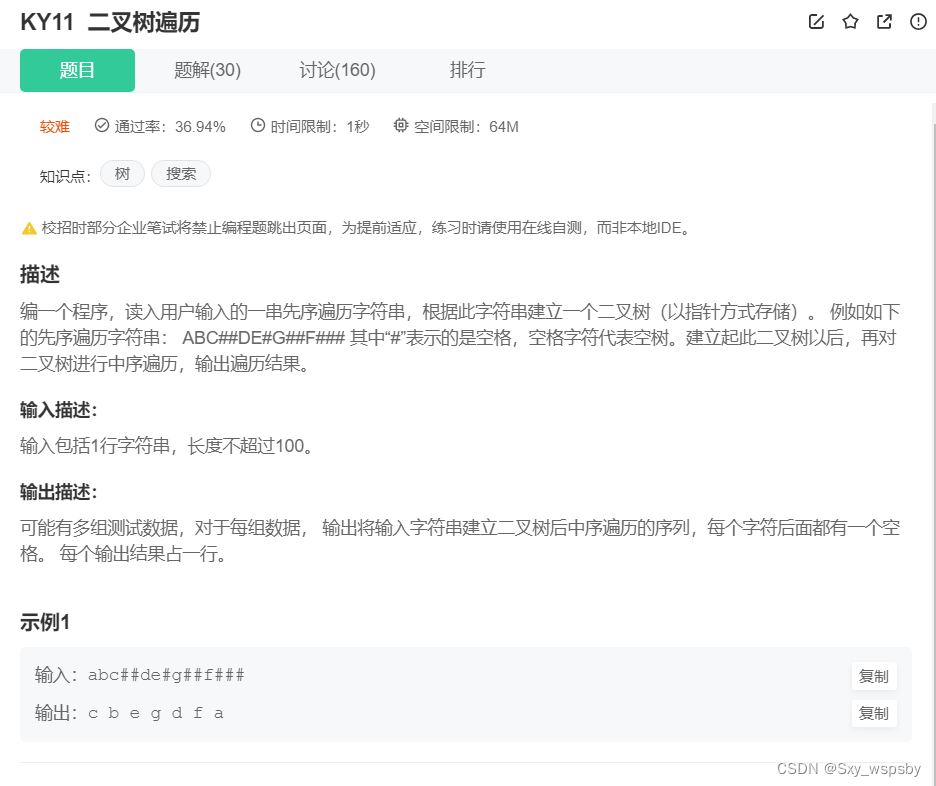
二叉树的遍历这道题我们在二叉树的构建中已经讲过并且还画了递归图，我们就快速的讲解一下这道题的难点即可。

#include <stdio.h>
#include <stdlib.h>
struct TreeNode
{
    char val;
    struct TreeNode*left;
    struct TreeNode*right;
};
struct TreeNode* rebuildTree(char* str,int* i)
{
    if (str[*i]=='#')
    {
        (*i)++;
        return NULL;
    }
    struct TreeNode*newnode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newnode->val = str[(*i)++];
    newnode->left = rebuildTree(str,i);
    newnode->right = rebuildTree(str,i);
    return newnode;
}
void middleOrder(struct TreeNode*root)
{
    if (root==NULL)
    {
        return;
    }
    middleOrder(root->left);
    printf("%c ",root->val);
    middleOrder(root->right);
}
int main() {
    char str[100];
    scanf("%s",str);
    int i = 0;
    struct TreeNode*tmp = rebuildTree(str,&i);
    middleOrder(tmp);
    return 0;
}

首先，因为牛客网上的这道题是IO型，所以需要我们自己写主函数以及数的结构等，所以我们在主函数中先定义了一个char类型的数组，因为题目告诉字符串长度不会超过100，所以我们就将数组的大小定为100即可，然后输入这个字符串，并且还需要一个下标记录每次取到字符串中字符的位置，这点与前序遍历那道题一样都是需要传下标的地址，这棵树建好后传来的是这棵树的根节点，然后我们在用中序遍历打印这个数，在重建这棵树的函数中，当我们遇到字符“#”时，我们就要返回一个NULL让上一个节点链接，在这里要注意下标的++，当遇到正常字符的时候，我们就创建一个新节点，新节点的值就是数组中下标位置的字符，放完后直接让下标++指向下一个字符，然后让这个新节点的左子树去链接下一个字符这里是用递归的形式链接左右子树，当字符串走完后各个节点链接完成返回这棵树。中序遍历只需要注意先去递归左子树然后再打印值然后递归右子树即可。

第九题：平衡二叉树力扣链接：力扣

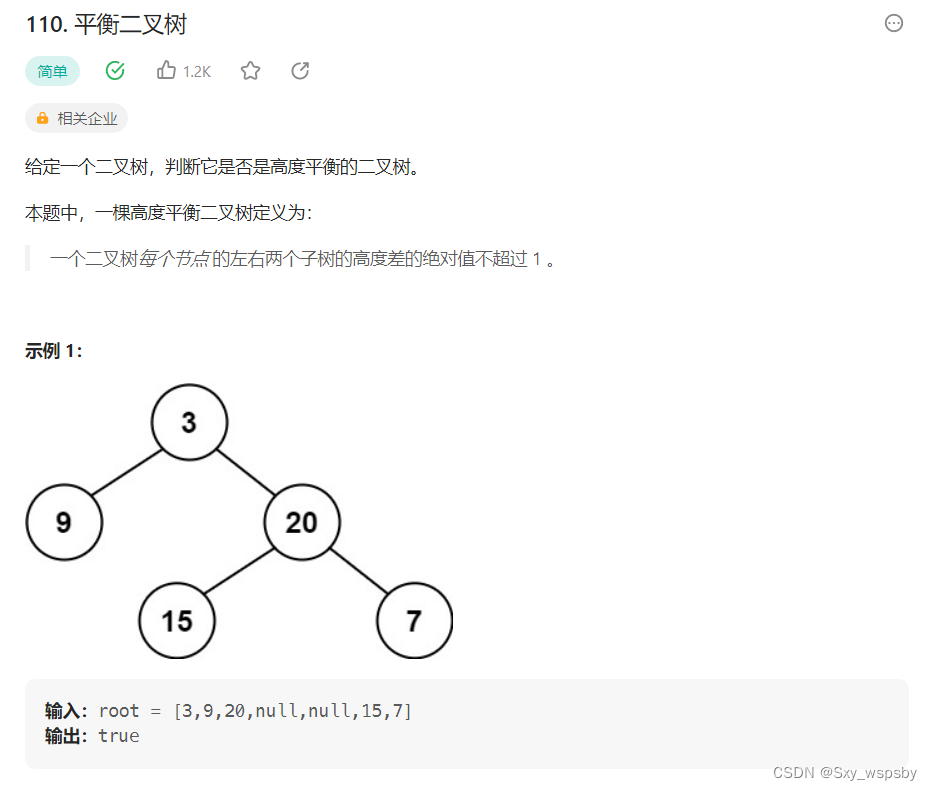我们从题目介绍可以看到判断是否为平衡二叉树就看左右两个子树的高度差有没有超过1，我们从这个角度出发，用之前写过的求二叉树高度的函数，分别去求这棵树左子树的高度和右子树的高度，然后用两个变量去接收高度，一旦两个高度的差值大于1我们就返回false。否则就去递归这棵树的左子树是否满足平衡二叉树的要求并且这棵树的右子树也要满足平衡二叉树的要求。

int TreeHeight(struct TreeNode* root)
{
    if (root==NULL)
    {
        return 0;
    }
    int leftheight = TreeHeight(root->left);
    int rightheight = TreeHeight(root->right);
    return leftheight>rightheight?leftheight+1:rightheight+1;
}
bool isBalanced(struct TreeNode* root){
     if (root==NULL)
     {
         return true;
     }
     int left = TreeHeight(root->left);
     int right = TreeHeight(root->right);
     if (abs(left-right)>1)
     {
         return false;
     }
     return isBalanced(root->left)&&isBalanced(root->right);
}

求二叉树的深度我们已经讲过就不在多说，主要看平衡二叉树函数，当这棵树为空时那么也是平衡二叉树，然后去用变量分别记录这棵树的左子树和右子树的高度，abs是求绝对值，我们用这个函数求左右高度的绝对值，一旦出现大于1的情况直接返回false。如果没有提前返回那就递归这棵树的左子树，看这棵树的左子树是否满足平衡二叉树的条件并且右子树也要递归去判断是否满足条件，有一个没满足就返回false。