目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

 首先介绍MATLAB部分的遗传算法的优化算法介绍：

       遗传算法的原理

       遗传算法GA把问题的解表示成“染色体”，在算法中也即是以二进制编码的串。并且，在执行遗传算法之前，给出一群“染色体”，也即是假设解。然后，把这些假设解置于问题的“环境”中，并按适者生存的原则，从中选择出较适应环境的“染色体”进行复制，再通过交叉，变异过程产生更适应环境的新一代“染色体”群。这样，一代一代地进化，最后就会收敛到最适应环境的一个“染色体”上，它就是问题的最优解。

一、遗传算法的目的
        典型的遗传算法CGA(Canonical Genetic Algorithm)通常用于解决下面这一类的静态最优化问题：考虑对于一群长度为L的二进制编码bi，i＝1，2，…，n；有

bi{0,1}L (3-84)

给定目标函数f，有f(bi)，并且

0

同时f(bi)≠f(bi+1)求满足下式

max{f(bi)|bi{0,1}L}

的bi。很明显，遗传算法是一种最优化方法，它通过进化和遗传机理，从给出的原始解群中，不断进化产生新的解，最后收敛到一个特定的串bi处，即求出最优解。

二、遗传算法的基本原理
        长度为L的n个二进制串bi(i＝1，2，…，n)组成了遗传算法的初解群，也称为初始群体。在每个串中，每个二进制位就是个体染色体的基因。根据进化术语，对群体执行的操作有三种：

1．选择(Selection)

这是从群体中选择出较适应环境的个体。这些选中的个体用于繁殖下一代。故有时也称这一操作为再生(Reproduction)。由于在选择用于繁殖下一代的个体时，是根据个体对环境的适应度而决定其繁殖量的，故而有时也称为非均匀再生(differential reproduction)。

2．交叉(Crossover)

这是在选中用于繁殖下一代的个体中，对两个不同的个体的相同位置的基因进行交换，从而产生新的个体。

3．变异(Mutation)

这是在选中的个体中，对个体中的某些基因执行异向转化。在串bi中，如果某位基因为1，产生变异时就是把它变成0；反亦反之。

        这里所指的某种结束准则一般是指个体的适应度达到给定的阀值；或者个体的适应度的变化率为零。
 

---

目标函数：

Min(F(x))=Min{H（i）}

F(x)=H（i）=H1m +H2m +H3m +H4m

其中设计变量：i1m ,i2m ,i3m ,i4m

目标函数：

Min(F(x))=Min{H（i）}

F(x)=H（i）=H1m +H2m +H3m +H4m

其中设计变量：i1m ,i2m ,i3m ,i4m

 优化结果：

螺杆总尺寸：H=

等速段最大圈数：i1m=

正弦加速度段最大圈数：i2m=

等加速度段最大圈数：i3m=

余弦加速度段最大圈数：i4m=

最大加速度：am=

螺杆对瓶子最大正压力：Pz=

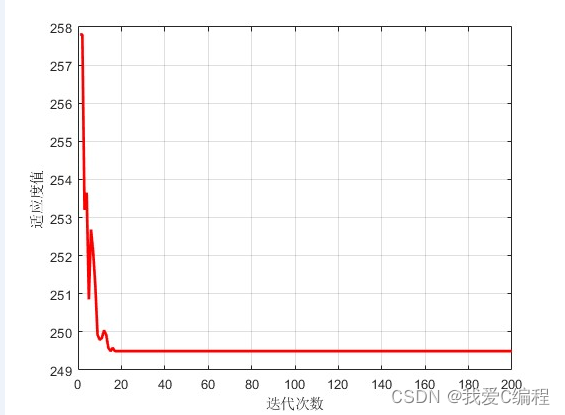
2.仿真效果预览

matlab2022a仿真如下：

 i1m =

    1.1283
i2m =

     2
i3m =

    3.0088
i4m =

    1.5044
am =

  149.6256
pz =

    2.2702
H =

  249.4948
 

3.MATLAB核心程序

p  = 26;%mm
cb = 42;
n  = 7;
fpd= 0.213;
fpc= 0.268;
fpb= 0.268;
g  = 9.8;
m  = 0.02;
G  = m*g;
es    = 0.75;
alpha = 24.749/180*pi;
gamma = 36.87/180*pi;
delta = 42/180*pi;
r2    = 9.2;
A     = 1 + fpb*sin(alpha)*csc(gamma);
B     = es - fpb*cos(alpha)*sin(delta)*csc(gamma);
C     = fpb*fpb*cos(alpha)*sin(delta)*csc(gamma);
hz    = 40; 
%%
%下面开始使用遗传优化算法
%根据遗传算法进行参数的拟合
MAXGEN = 200;
NIND   = 5000;
Nums   = 4;
Chrom  = crtbp(NIND,Nums*10);
Areas  = [[1.5,2,4,2]/4;
          [1.5,2,4,2]];

FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];

for a=1:1:NIND 
    %计算对应的目标值
    %初始值
    epls       = func_obj(0,0,0,0);
    E          = epls;
    Js(a,1)    = E;
end
Objv  = (Js+eps);
gen   = 0; 

while gen < MAXGEN;   
      gen
      Pe0 = 0.9;
      pe1 = 0.02;
      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   
      
      i1ms=[];
      i2ms=[];
      i3ms=[];
      i4ms=[];
      for a=1:1:NIND  
          i1m = phen1(a,1);
          i2m = phen1(a,2);
          i3m = phen1(a,3);
          i4m = phen1(a,4);
          am  = pi*n^2*(cb-p)/(2*i2m+pi*i3m+2*i4m);
    
          %约束设置
          %约束1
          SCALE = 3;
          if A+B*fpc > C*fpd
             if am > fpd*g
                i1m = SCALE*i1m; 
                i2m = SCALE*i2m;
                i3m = SCALE*i3m;
                i4m = SCALE*i4m;
             end
          end
          if A+B*fpc < C*fpd
             if am < fpd*g
                i1m = i1m/SCALE; 
                i2m = i2m/SCALE;
                i3m = i3m/SCALE;
                i4m = i4m/SCALE;                 
             end          
          end     
          
          %约束2
          tmps = r2/fpd;
          if hz < tmps
          end
          
          %约束3
          if am*pi*n/2/i2m > 10
             i2m = am*pi*n/20;
          end
          
          %约束4
          if i1m<0  ;i1m=0;end 
          if i1m>1.5;i1m=1.5;end
          
          if i2m<0  ;i2m=0;end 
          if i2m>2  ;i2m=2;end 
          
          if i3m<0  ;i3m=0;end 
          if i3m>4  ;i3m=4;end  
          
          if i4m<0  ;i4m=0;end 
          if i4m>2  ;i4m=2;end 
          
          %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
          %计算对应的目标值
          epls    = func_obj(i1m,i2m,i3m,i4m);
          E       = epls;
          JJ(a,1) = E;
          
          
          i1ms=[i1ms,i1m];
          i2ms=[i2ms,i2m];
          i3ms=[i3ms,i3m];
          i4ms=[i4ms,i4m]; 
      end 
      
      Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 

      %保存参数收敛过程和误差收敛过程以及函数值拟合结论
      index1      = isnan(JJ);
      index2      = find(index1 == 1);
      JJ(index2)  = [];
      Error2(gen) = min(JJ);
end 

%根据最优的参数值，计算各个指标
[V,I] = min(JJ);
i1m = i1ms(I);
i2m = i2ms(I);
i3m = i3ms(I);
i4m = i4ms(I);

 

am  = pi*n^2*(cb-p)/(2*i2m+pi*i3m+2*i4m);
pz  = abs(G*(fpd*g-am)/(g*(A+B*fpc-C*fpd)));
H   = func_obj(i1m,i2m,i3m,i4m);

i1m
i2m
i3m
i4m
am
pz
H
02_046m

4.完整MATLAB

V