0、引言
本文介绍一种能够偶快速查找字符串的树形数据结构-----字典树。介绍其原理,以及通过leetcode208题目这个实例,用数组动手实现一棵字典树,并完成其增、查字符串、查字符串前缀的功能。
1、字典树的应用场景
询问一个单词b,问b是否出现在n个给出的单词中,你会如何去求呢?暴力搜索显然复杂度太高,我们可以把问题转换成查字典的操作:平时是怎么查字典的呢?
如果你要在字典中查找单词“Avalon”,你是不是先找到首字母为‘A’的部分,然后再找第二个单词为‘V’的部分······最后,你可能可以找到这个单词,当然,也有可能这本词典并没有这个单词。你想想看,你这样子的查单词的方式是不是比你从词典第一页开始查询到最后一页寻找单词“Avalon”要高效多了?那我们可不可以也建一本"字典"呢?
2、字典树的介绍
字典树(TrieTree),是一种树形结构,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串,如01字典树)。主要思想是利用字符串的公共前缀来节约存储空间。很好地利用了串的公共前缀,节约了存储空间。字典树主要包含两种操作,插入和查找。
在这里,我们借用大佬http://t.csdn.cn/Z1rt2文章的图片例子来说明其原理。
比如,我们要怎么用树存下单词"abc",“abb”,“bca”,"bc"呢?见图

在图中,红点代表有一个以此节点为终点的单词。然后,我们如果要查找某个单词如s=“abc”,就可以这样

在这里,s=“abc” 的每一个字母都在树中被查到了,并且最后一个点是红色代表有一个在此结束的单词,查询成功。而 s=“bb” 的第二个字母没有在相应位置被查到,因此"bb"不在字典中。至于s=“ab” 虽然单词中每个点都被查到了,但是由于结尾的字母在树中没有标红,因此也是不在字典中。时间复杂度为log级别,比暴力快多了。
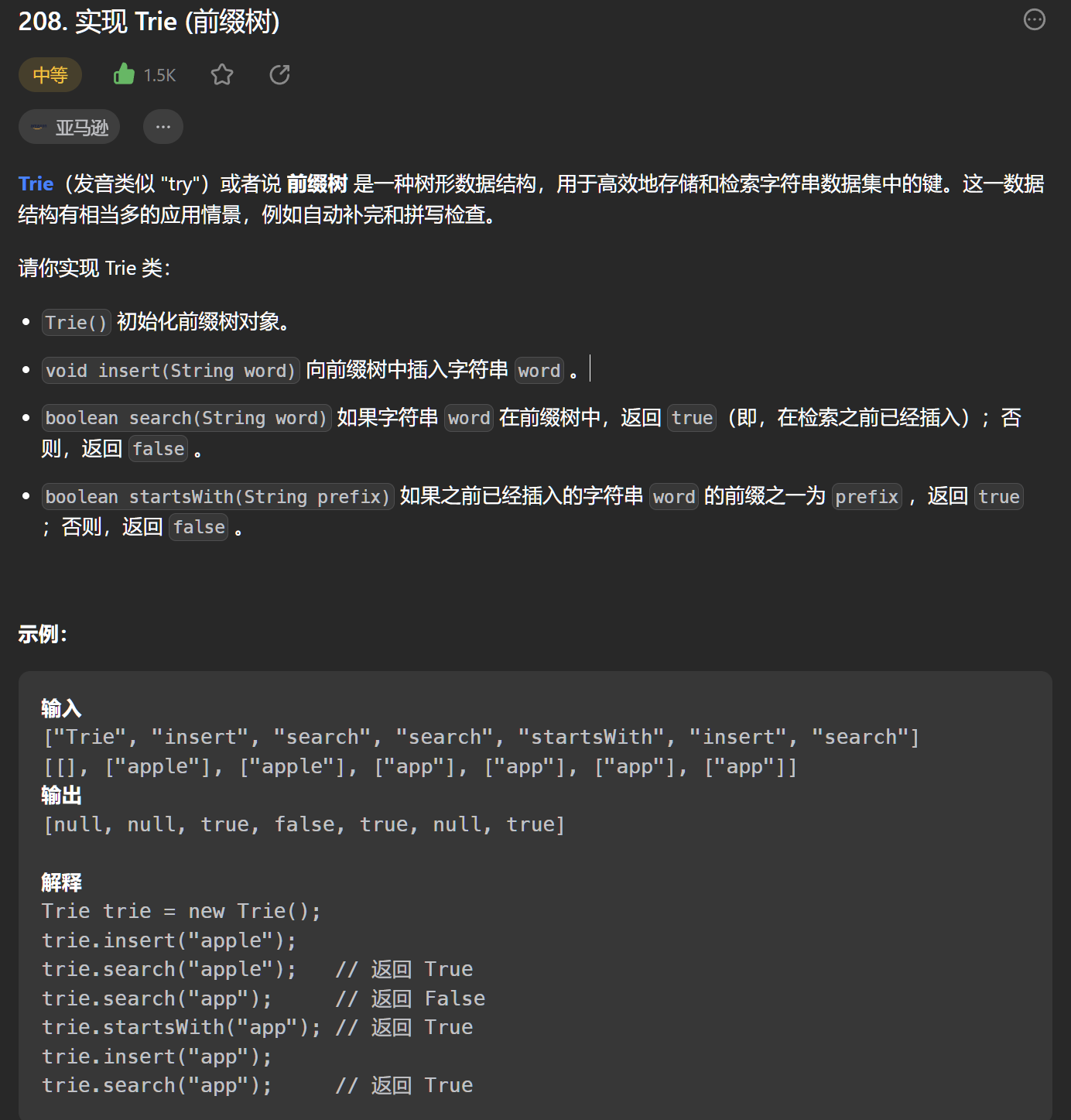
3、字典树的代码实现(leetcode208. 实现 Trie (前缀树))
力扣有一道现成的实现前缀树的题目,其中包含了初始化前缀树、往前缀树插入某单词、搜索前缀树是否存在某单词、搜索前缀树是否存在某前缀,这四个模块,用这个例子下面我们来实现一下这个字典树。
3.1 初始化
对于每个前缀树Trie类的对象,该对象有两个属性:
(1)类型是Trie的大小是26的数组children,象征着26个字母。
比如,如果存入一个‘b’,那么就在'b' - 'a'的位置,即索引1的位置创建一个Trie类的对象即可。
用这种方式来标识是否存在某个字母👆
(2)布尔类型的变量isEnd
因为后面需要判断是否存在“完整单词”与“单词前缀”,因此要设立isEnd,来标志是否是叶子节点。
比如插入了aabbc,如果搜索aabbc,沿着树找到c,发现isEnd是true,说明存在这个单词。如果搜aabb,能找到b,但isEnd是false,因此不存在这个单词,仅仅存在单词前缀。
代码如下:
//1、初始化26个字母节点数组、2、判断是否为叶子节点的标志
private Trie[] children;
private boolean isEnd;
//每个Trie类的对象有两个属性:
public Trie() {
children = new Trie[26];
isEnd = false;//初始化为非叶子节点,后面如果判断为叶子、再设为true
}3.2 插入字符串单词
插入单词,首先我们要拿到插入单词的Trie对象。
然后对于插入的word,遍历其每一个字母,在前缀树里往深处添加。代码很容易理解:
public void insert(String word) {
Trie node = this;//拿到要插入单词的前缀树对象node
for(int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
int index = ch - 'a';
if(node.children[index] == null){
node.children[index] = new Trie();
}
node = node.children[index];//无论是否为null,node都指向下一层Trie节点
}
node.isEnd = true;//最后一层,则为True
}3.3 在前缀树中搜索单词
我们在前缀树里,搜索某个单词,例如在aabb里:搜索ac,那么查到c的时候,children的位置应该是个空值,返回值是null。
如果搜索aab,那就是虽然能搜到,但isEnd是false。
如果搜索aabb,不仅能搜到,而且isEnd为true。
因此,我们可以写一个函数,返回的就是搜索前缀树的时候,搜索到最深处的对象node。
这样,如果node为空,就是不存在。node不为空:根据isEnd判断是否是完整单词or前缀单词即可!
代码如下:
//查是否含有某个完整单词的函数:
public boolean search(String word) {
Trie node = searchPrefix(word);
if(node == null || !node.isEnd){//根本没这个单词,或者,虽然含有有这个单词但不是完整的
return false;
}else{
return true;
}
//比如在aapp里搜索ab或者aap,那就是没这个单词
}
//查是否有某前缀的函数:
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;//只要存在就行,不是结尾也没关系。
//比如再aaple里搜索aap,那就是有这个前缀。
}
//核心函数!!!
private Trie searchPrefix(String word){
Trie node = this;
for(int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
int index = ch - 'a';
if(node.children[index] == null){
return null;
}
node = node.children[index];
}
return node;
}4、完整代码
class Trie {
//1、初始化26个字母节点数组、2、判断是否为叶子节点的标志
private Trie[] children;
private boolean isEnd;
//每个Trie类的对象有两个属性:
public Trie() {
children = new Trie[26];
isEnd = false;//初始化为非叶子节点,后面如果判断为叶子、再设为true
}
public void insert(String word) {
Trie node = this;
for(int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
int index = ch - 'a';
if(node.children[index] == null){
node.children[index] = new Trie();
}
node = node.children[index];//无论是否为null,node都指向下一层Trie节点
}
node.isEnd = true;//最后一层,则为True
}
public boolean search(String word) {
Trie node = searchPrefix(word);
if(node == null || !node.isEnd){//根本没这个单词,或者,虽然含有有这个单词但不是完整的
return false;
}else{
return true;
}
//比如在aapp里搜索ab或者aap,那就是没这个单词
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;//只要存在就行,不是结尾也没关系。
//比如再aaple里搜索aap,那就是有这个前缀。
}
private Trie searchPrefix(String word){
Trie node = this;
for(int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
int index = ch - 'a';
if(node.children[index] == null){
return null;
}
node = node.children[index];
}
return node;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/





![数据结构05:树的定义与双亲表示法[持续更新中]](https://img-blog.csdnimg.cn/baefcca43f8a484e9da5695a0dbfca1d.png)