1.应用:
- 教学计划(先修什么才能修什么课程)
- 社交网络
- 地图导航
2.什么是图? 顶点(有穷非空个)+顶点的边 ,抽象为G=(V,E) =(Vert,Edge)
1.无向图: 点到点都可以到达 表示为(vi,vj)
2.有向图 只能一个点到另外一个点 表示为<vi,vj>
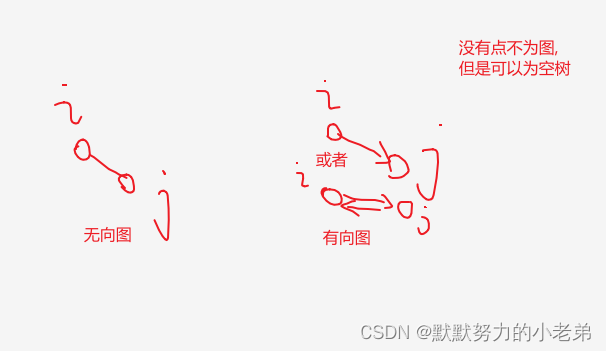
又分为:
1.非带权图(上面的例子就是)
2.带权图(网图)
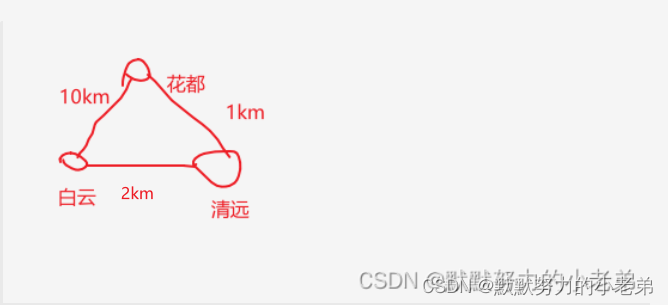
又又分为:
1.稠密图(边多) 只是相对概念
2.稀疏图(边少)
3.几个概念
1.邻接(从本节点可以到达另外一个节点) 邻接点(可到达的点),依附(与邻接相反的概念) 如图
无向图: A 邻接C和B
有向图: A邻接B和C D邻接A
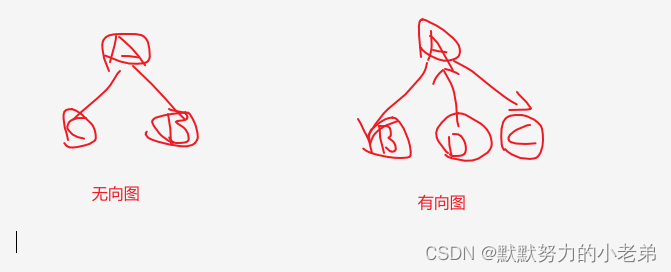
- 完全图
1. 无向完全图 任意两个点有边
边数=n*(n-1)/2 (n是节点数)
2. 有向完全图 任意两点有方向相反的两条弧
边数=n*(n-1)

- 度(无向图):边数
入度(有向图) 进入弧头有多少个
出度(有向图) 出去弧头有多少个
4,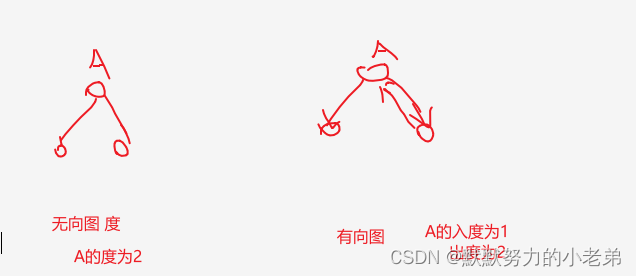
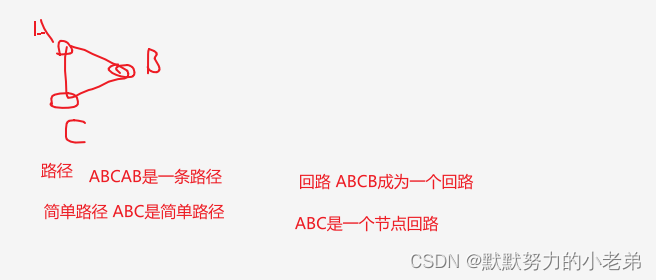
- 路径:顶点的序列
简单路径: 点不重复走
回路:成一个环形
简单回路:成环状但是点不重复
5.路径长度(边的权相加)
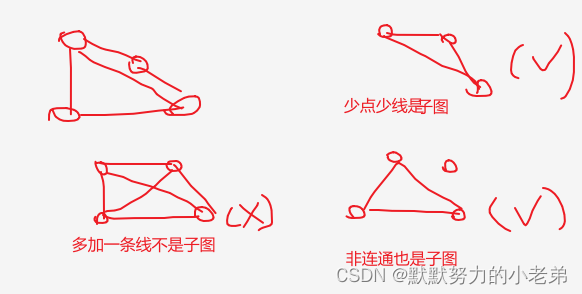
6.子图 G’(V’,E;) 属于 G(V,E)这个图
7.连通顶点:之间有路径
连通图: 任两点可以访问(可以间接通过其他节点)
非连通图: 任两点不能连通
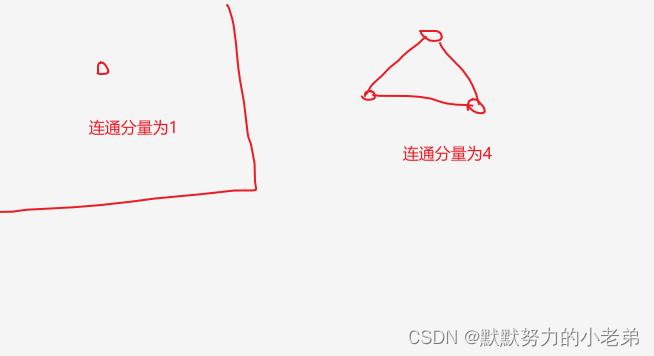
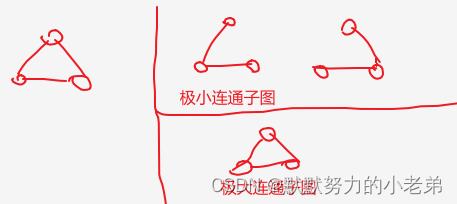
连通分量: 连通 后 里面的元素 (是图的极大连通子图)
极大连通子图: 加一个点连通 去边不连通
(有向)强连通分量: ^同理
4.图的深度优先遍历(需要stack栈辅助) 一边入栈一边访问 如果访问完了出栈访问
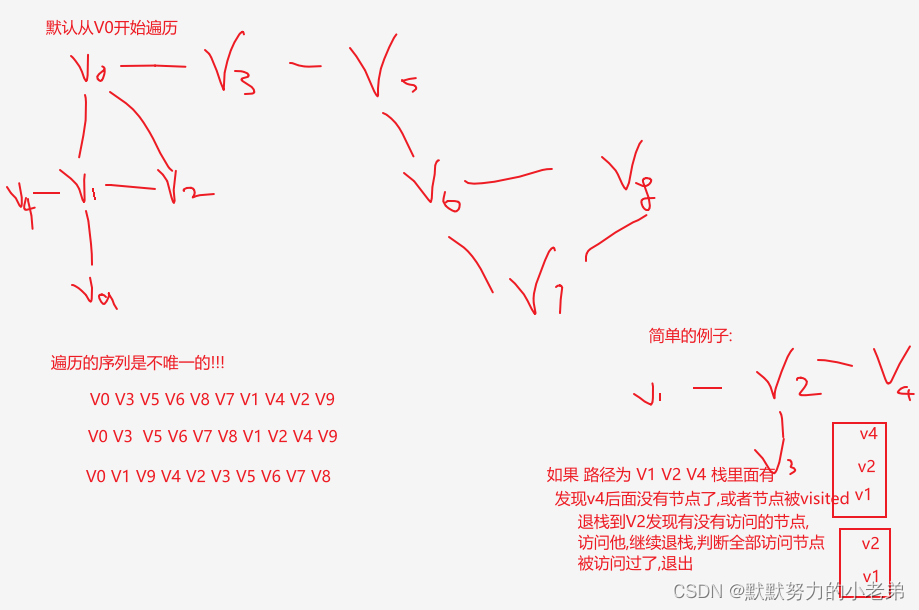
5.图的广度优先遍历(像树层次遍历)(需要队列辅助) 先访问相邻的全部节点后访问,相邻的相邻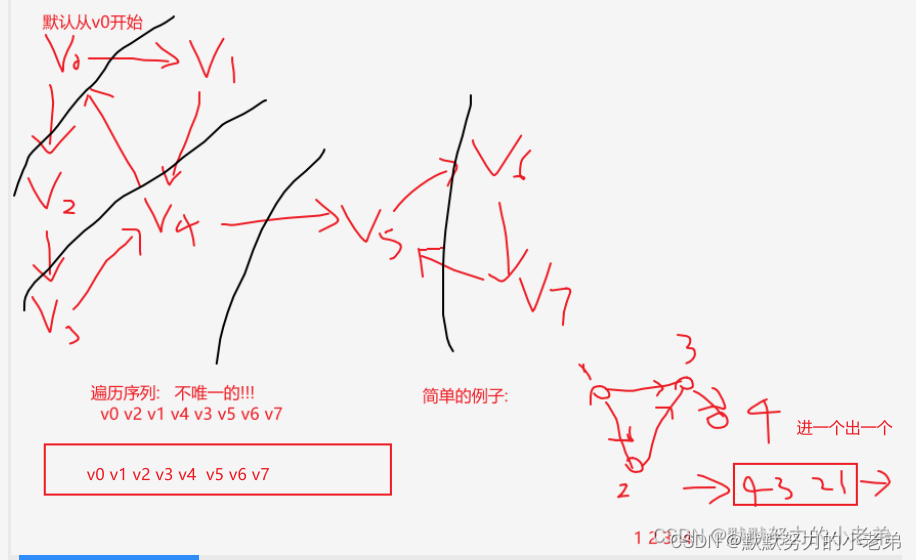
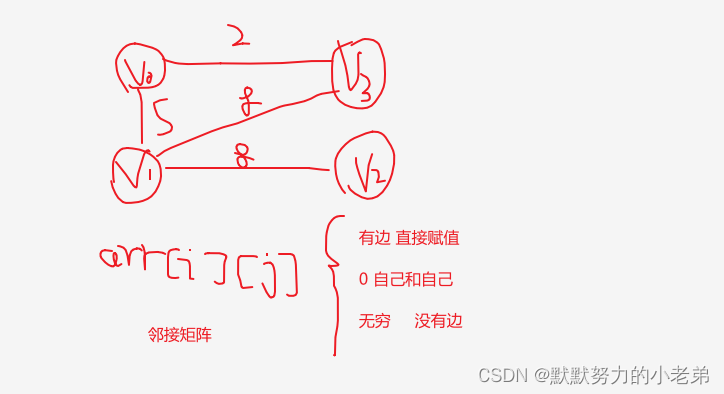
6.图的邻接矩阵(顺序存储存储图)(一维数组)(稠密图)
1.一维(存顶点)+二维(顶点之间的关系)
edge[i][j]=1 连接的 ------如果----- =0 不连接
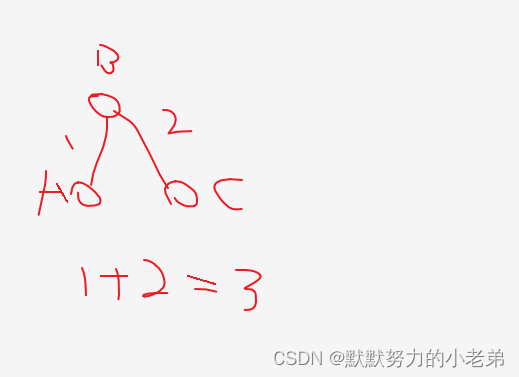
2.怎么求每个节点的度?(无向图) 一行的值相加即可 如: 上面 v0的度为2 v1的度为3
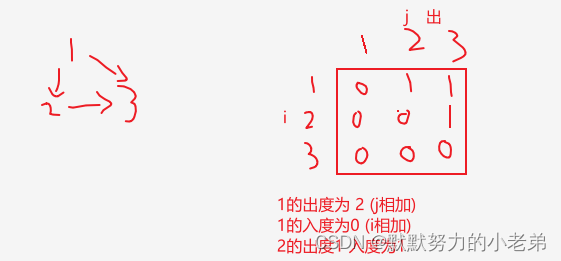
(有向图) j是出度 i是入度
3.网图的(带权)(需要多一个存全都二维[])
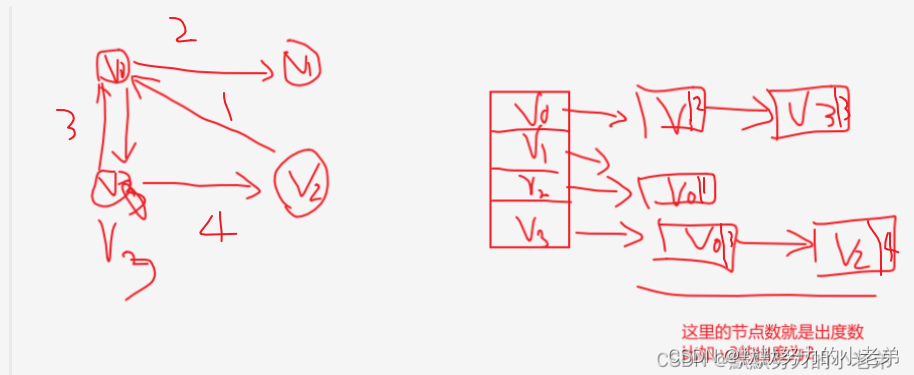
7.图的邻接表(改进了连接矩阵空间复杂度为O(n^2) 存稀疏图大量浪费空间)
1.无向 空间复杂度为O(n+e) 有n个顶点 e条边
2.有向的(链表的的指向,代表图箭头的方向)
3.带权的(2的基础上链表加个权值字段)
8.最小生成树(实际运用)(把图转换为树)
1.定义 (是极小连通子图 含 n-1条边)
2.代价: 权之和最小
3.在实际的应用(光纤布线,需要最短的距离,物流站点的设置)
9.最小生成树值Prim算法(无向图)(加入节点作为一个整体)必须访问全部节点结束
关键字: 整体
- 步骤:
1. 从任意一点出发
2. 找最短边,然后加入节点作为一个整体!!!(不能为环)
例如:
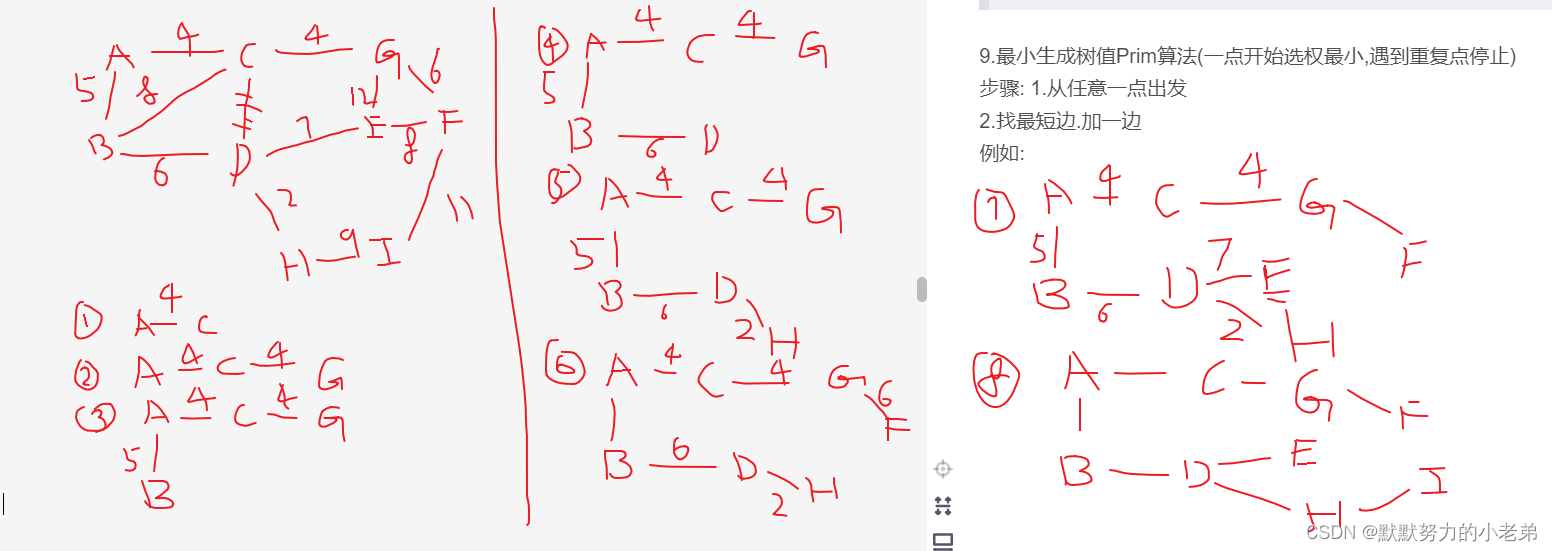
第二个例子 (好办法,使用圈圈辅助,容纳为一个整体)
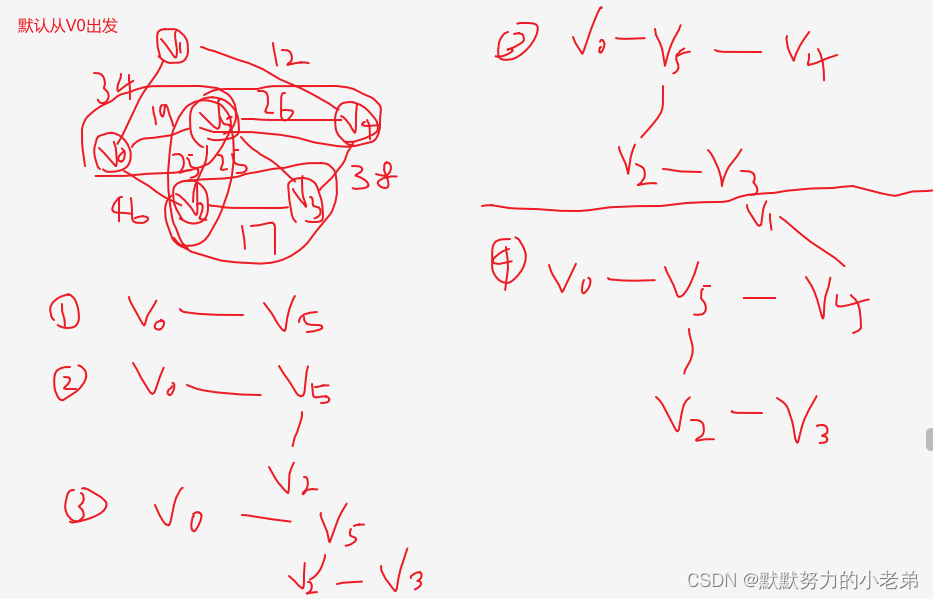
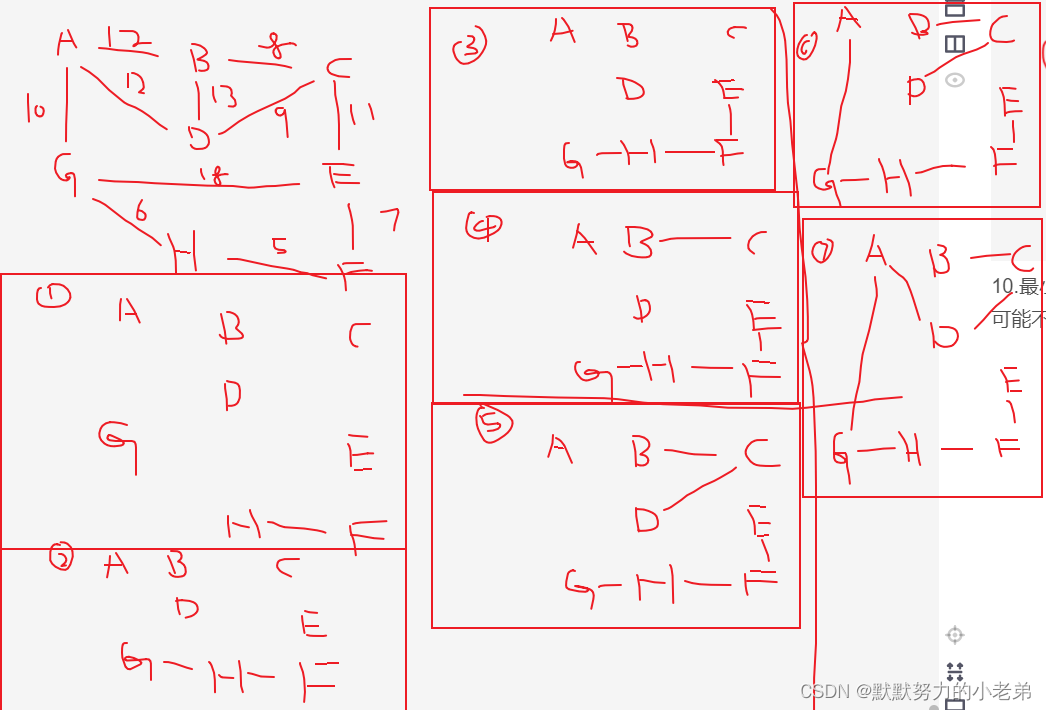
10.最小生成树值Kruskal算法(无向图)(全部点作为整体,分别在点与点直接连接)(适合边多的)(两个算法,生成树可能不一样,但权值加起来是一样的)
关键字: 部分
步骤:
1.画出全部点
2.全部边的权值放到一个数组里面从小到大排序
3.找到这个图最小权值的边连接,如果成环,剔除这个边
4.不停做3…
11.最小生成树之Dijkstra算法(上面两种算法是给你一个图生成树,求任意两点的最短距离)(不用于负权值) (不必访问所有顶点)复杂度O(n^2) 关键字: 以前
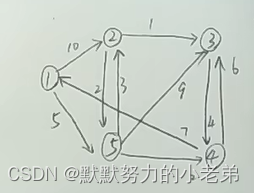
下面是求1->3的最短路径(需要从以前路径比较[看看是否到达这个点])

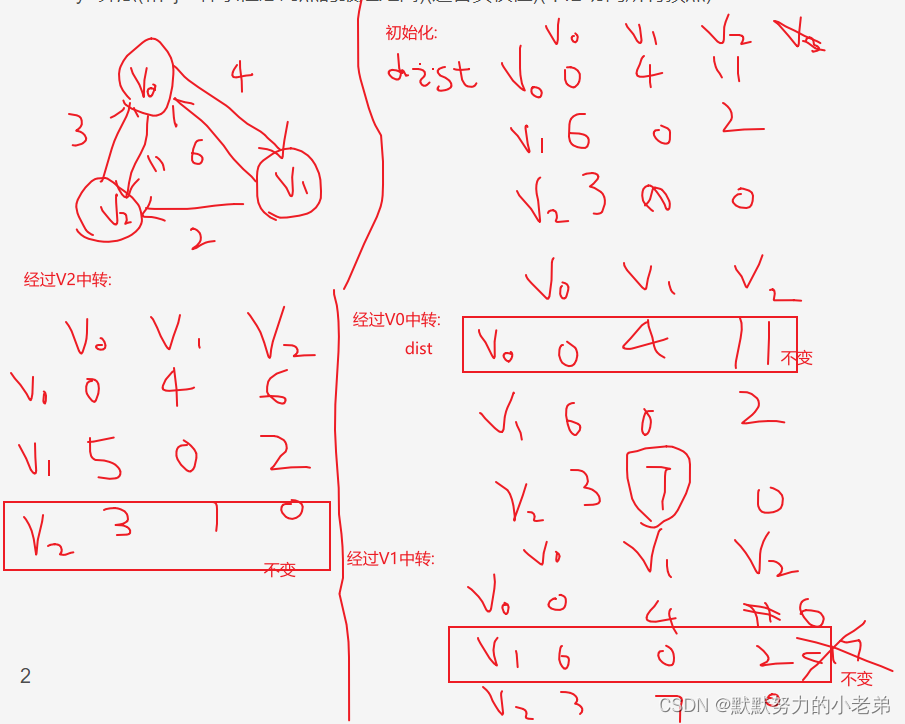
12.Floyd算法(和dj一样求任意两点的最短距离)(适合负权值)(不必访问所有顶点)(!!!遍历全部节点作为中转节点,如果中转后更小改值) 关键字: 中转
13.AOV网(activity on vertex network)(不一定有起点和终点)
- 工程:所有工程有子工程,必须完成子过程才能完成工程(说人话就是,一件事情有他的前提条件,必须先做完切菜洗菜,才能炒菜)
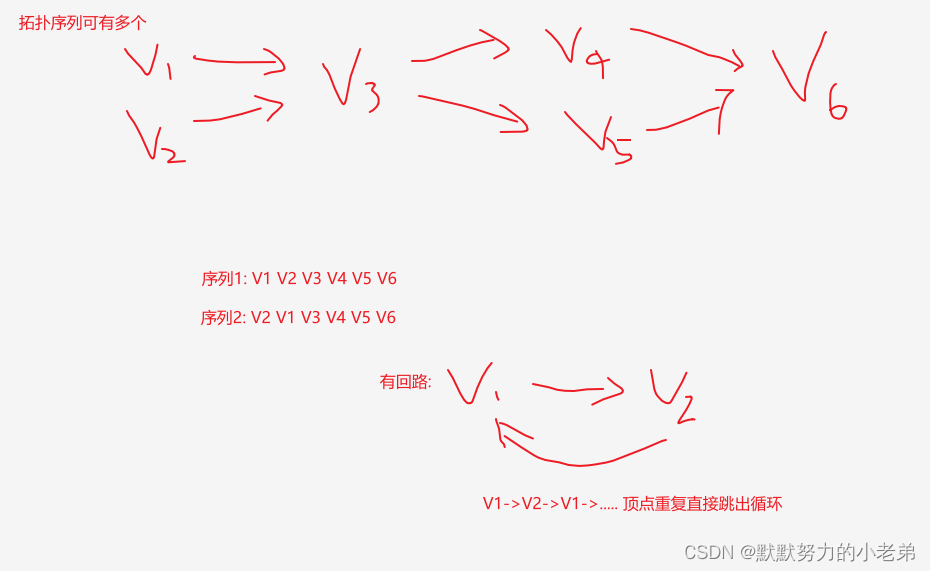
- 使用拓扑排序(有向无环图)(topology拓扑学 位置学的英译)(一个点在path不重复出现)判断AOV网是否有回路
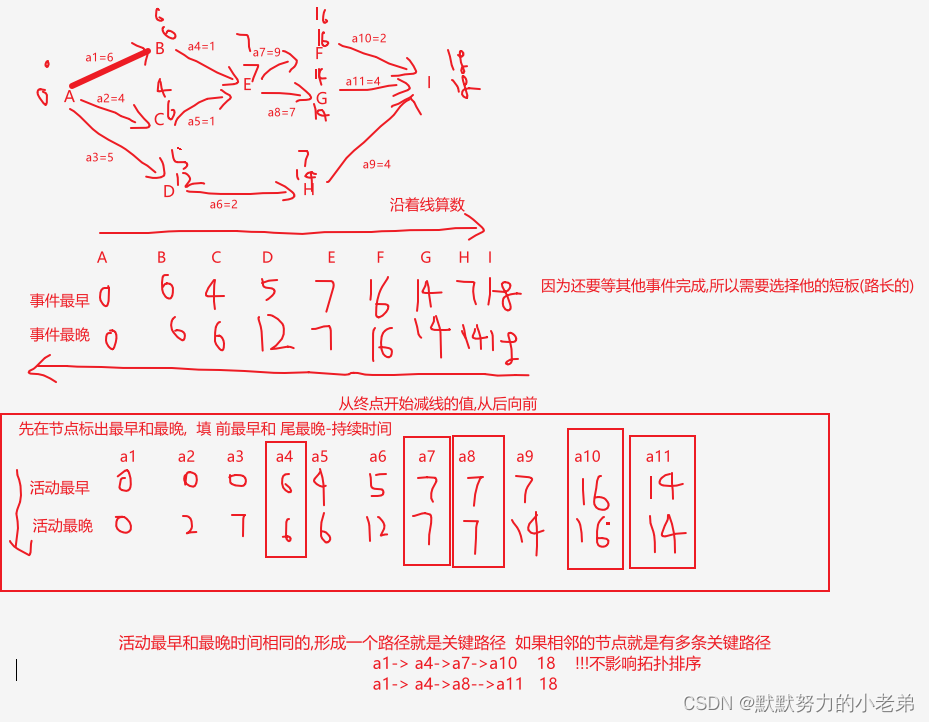
14.AOE网(AOE+权[时间] ) 边上的每个活动都有持续时间 activity on edge network(一定有源点[入度为0]和终点[出度为0])
1.解决的问题: 总工程最长(短)要多少时间, 缩短工期加快哪些活动更有效
2.关键路径(最长的路径,不同方案下)
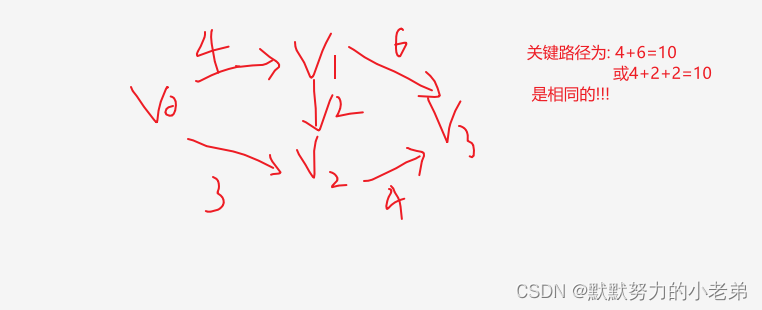
3.(算法过程而不是肉眼看到的)