一、光照模型
● 一种模拟自然光照过程的计算机模型
● 本次课程可以这样理解:光线与物体表面的作用
● 分类
○ 基于物理的光照模型(PBR)(有可依据的公式)
○ 经验模型(进行了一些近似、模拟,所以会不准)
光照模型发展历史

二、局部光照模型
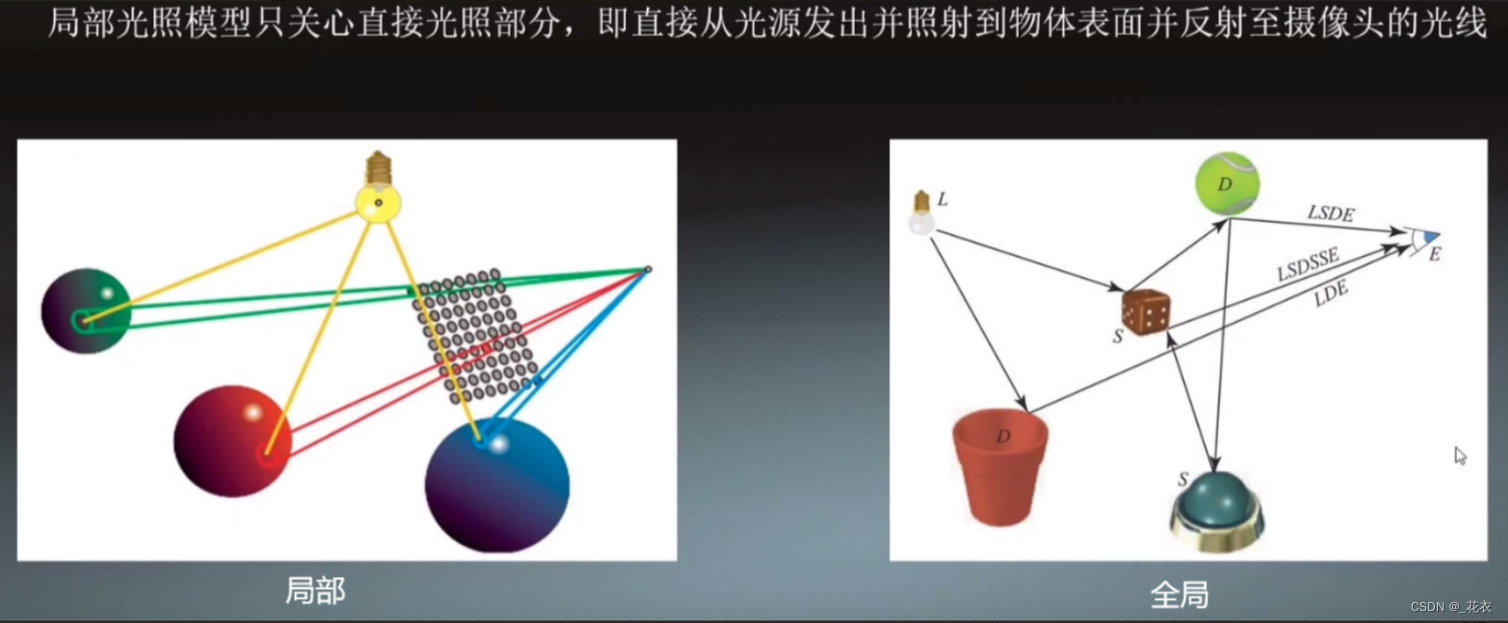
1.局部光照的定义
● 只考虑光源的影响,不考虑光线多次反射
● (对应的概念:全局光照=直接光照+间接光照)
①漫反射
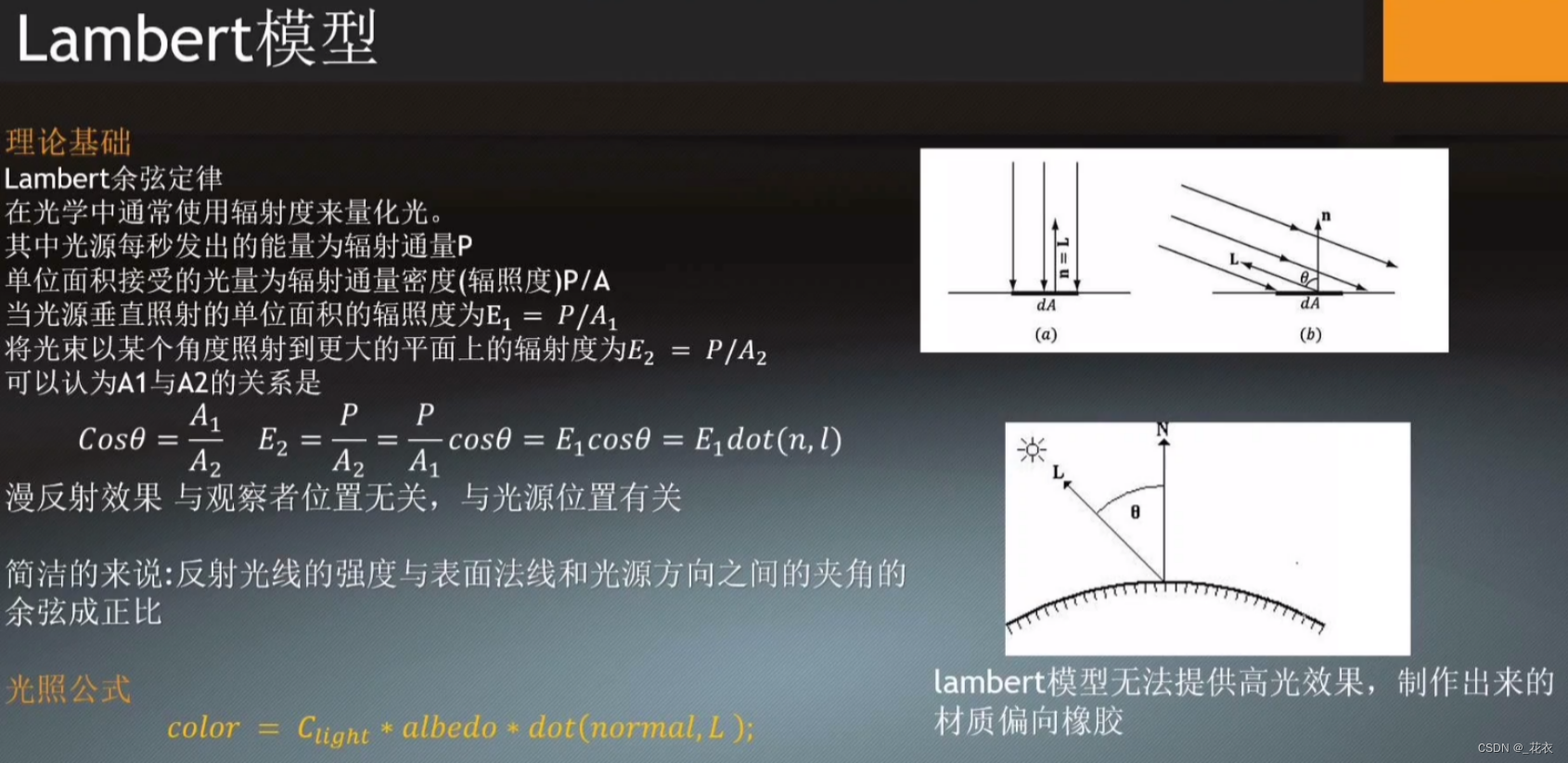
计算:Lambert余弦定理

● 补充:
○ 首先其中对应GAMES101中的辐射度量学中的一个概念
■ Irradiance翻译为辐照度
○ Lambert余弦定律结论:n(法线方向)和 l(光照方向)的夹角决定了明暗
②高光项(镜面反射)

● 高光项中,和光的方向l有关
● 补充
○ blinn-phong模型中,引入了“半程向量”,用来代替反射的计算
○ gloss指数的作用:控制高光的大小。(就是GAMES101-blinn-phone模型中的p指数)
③环境光

④自发光

3.局部光照总体效果总览

三、经典光照模型
1.Lambert模型
//定义顶点shader
v2f vert(a2v v)
{
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
//把法线转化到世界空间
float3 worldNormal = mul(v.normal, (float3x3)_World2Object);
//归一化法线
worldNormal = normalize(worldNormal);
//把光照方向归一化
fixed3 worldLightDir = normalize(_WorldSpaceLightPos0.xyz);
//根据兰伯特模型计算顶点的光照信息,dot可能有负值,小于0的部分可以理解为看不见,直接取0
fixed3 lambert = max(0.0, dot(worldNormal, worldLightDir));
//最终输出颜色为lambert光强*材质diffuse颜色*光颜色
o.color = fixed4(lambert * _Diffuse.xyz * _LightColor0.xyz, 1.0);
return o;
}
//定义片元shader
fixed4 frag(v2f i) : SV_Target
{
return i.color;
}
//使用vert函数和frag函数
#pragma vertex vert
#pragma fragment frag
ENDCG
}
}
2.Phone模型

//顶点着色器
v2f vert(a2v v){
v2f o;
//顶点转换到裁切空间坐标
o.pos = UnityObjectToClipPos(v.vertex);
//顶点法线转换到世界空间
o.worldNormal = UnityObjectToWorldNormal(v.normal);
//顶点位置转换到世界空间坐标
o.worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;
//顶点着色器纹理的UV坐标
o.uv = v.texcoord.xy * _MainTex_ST.xy + _MainTex_ST.zw;
return o;
}
//片元逐像素实现
fixed4 frag(v2f i) : SV_Target {
//世界空间下法线方向
fixed3 worldNormal = normalize(i.worldNormal);
//世界空间下光照方向
fixed3 worldLightDir = normalize(UnityWorldSpaceLightDir(i.worldPos));
//tex2D()纹理采样
//得到材质反射率
fixed3 albedo = tex2D(_MainTex, i.uv).rgb * _Color.rgb;
//得到光照下材质反射率
fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz * albedo;
//计算环境光
fixed3 diffuse = _LightColor0.rgb * albedo * max(0, dot(worldNormal, worldLightDir));
fixed3 viewDir = normalize(UnityWorldSpaceLightDir(i.worldPos));
fixed3 halfDir = normalize(worldLightDir + viewDir);
//计算高光反射
fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(max(0,dot(worldNormal, halfDir)), _Gloss);
return fixed4(ambient + diffuse + specular, 1.0);
}
3.Blinn-Phone模型
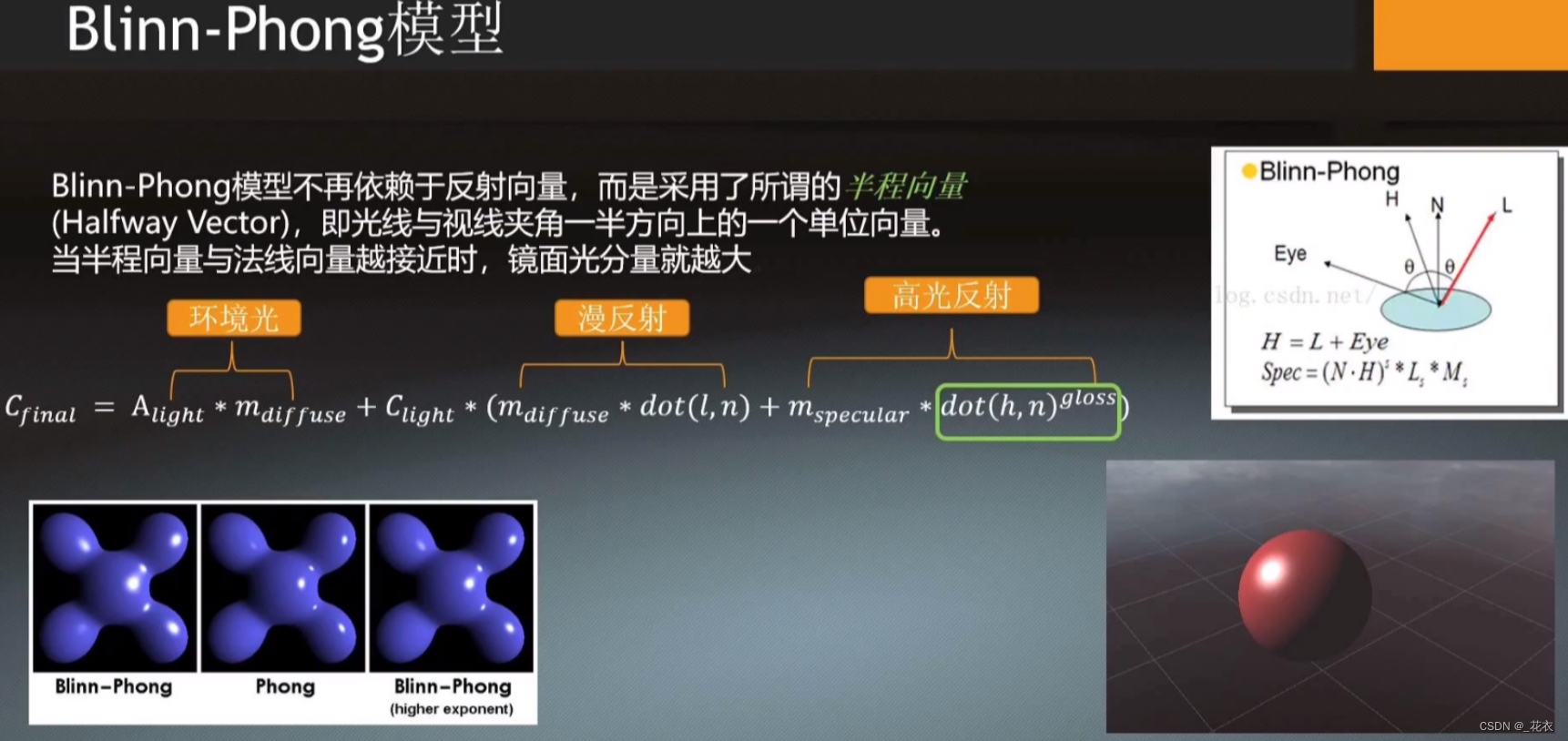
● 对Phong模型进行了改进,不用反射向量来计算高光
● 关键:引入了半程向量h
● 半程向量的计算:光照方向和观察方向相加,再归一化
● NdotH:就是半程向量和法线向量的夹角的余弦。得到高光方向
4Phong模型和Blinn-Phong模型的区别

5.Gourand模型

6.Flat模型

7.提到的光照模型的展示

能量守恒在基础光照模型中的作用
首先搞懂渲染中能量守恒的概念。
● 传统光照模型中,漫反射部分认为光会被均匀的反射到不同的方向。
● 但是在微表面理论中认为,达到微观尺度之后任何平面都可以用被称为微平面(Microfacets)的细小镜面来进行描绘。根据平面粗糙程度的不同,这些细小镜面的取向排列可以相当不一致。如图,产生的效果就是:一个平面越是粗糙,这个平面上的微平面的排列就越混乱。这些微小镜面这样无序取向排列的影响就是,当我们特指镜面光/镜面反射时,入射光线更趋向于向完全不同的方向发散(Scatter)开来,进而产生出分布范围更广泛的镜面反射。而与之相反的是,对于一个光滑的平面,光线大体上会更趋向于向同一个方向反射,造成更小更锐利的反射:
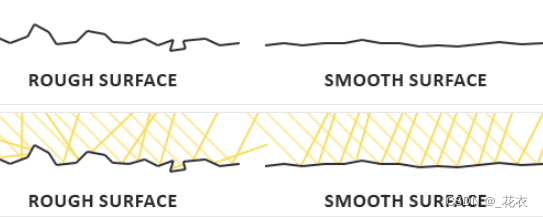
● 我们假设一个粗糙度的参数,然后用统计学的方法来概略的估算微平面的粗糙程度。基于一个平面的粗糙度来计算出某个向量的方向与微平面平均取向方向一致的概率,这个向量就是Blinn-Phong模型中的半程向量 h 。
● 微平面的取向方向与中间向量的方向越是一致,镜面反射的效果就越是强烈越是锐利。然后再加上一个介于0到1之间的粗糙度参数,这样我们就能概略的估算微平面的取向情况了:
微平面近似法使用了这样一种形式的能量守恒(Energy Conservation):出射光线的能量永远不能超过入射光线的能量(发光面除外)。如图示我们可以看到,随着粗糙度的上升镜面反射区域的会增加,但是镜面反射的亮度却会下降。如果不管反射轮廓的大小而让每个像素的镜面反射强度(Specular Intensity)都一样的话,那么粗糙的平面就会放射出过多的能量,而这样就违背了能量守恒定律。这也就是为什么正如我们看到的一样,光滑平面的镜面反射更强烈而粗糙平面的反射更昏暗。

● 能量守恒(Energy Conservation):出射光线的能量永远不能超过入射光线的能量(发光面除外)。
● 如上图,随着粗糙度的上升镜面反射区域的会增加,但是镜面反射的亮度却会下降。如果不管反射轮廓的大小而让每个像素的镜面反射强度(Specular Intensity)都一样的话,那么粗糙的平面就会放射出过多的能量,而这样就违背了能量守恒定律。
而能量守恒对于传统光照模型的作用,我认为可以这么说
● 让人们人知道经验模型的不准确的地方,以改良模型,来实现更真实的效果。
● 引出PBR的概念。
● 为了遵守能量守恒定律,我们需要区分镜面反射(反射),和漫反射(折射)。
● 当一束光线碰撞到一个表面的时候,它就会分离成一个折射部分和一个反射部分。
○ 反射部分就是会直接反射开来而不会进入平面的那部分光线,这就是我们所说的镜面光照。
○ 折射部分就是余下的会进入表面并被吸收的那部分光线,这也就是我们所说的漫反射光照