1. 正态分布简介

正态分布应该是概率论和数理统计中最重要的一类概率分布，最早的完整论述是由数学王子高斯提出，高斯主要用来分析观测的误差分析中推导出正态分布。虽然随着概率统计学的发展，自然分布形式多种多样，但是正态分布仍然可以说是最重要的自然分布。
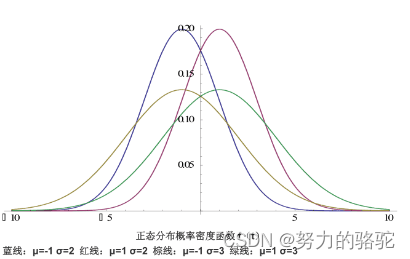
一维正态分布的概率密度函数如下所示：
$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}$$
上述概率密度图形如下图所示。

1. 正态分布的数字特征

正态分布的期望也就是均值如下式所示。
$$\begin{array}{rl}E(x)& ={\int }_{-\infty }^{\infty }xf(x)dx={\int }_{-\infty }^{\infty }x\cdot \frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\\ & ={\int }_{-\infty }^{\infty }\frac{x-\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx+{\int }_{-\infty }^{\infty }\frac{\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\end{array}$$
第一个积分式中用变量变换$z=\frac{x-\mu }{\sigma }$
$$\begin{array}{rl}{\int }_{-\infty }^{\infty }\frac{x-\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx& ={\int }_{-\infty }^{\infty }z\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}{z}^2}\sigma dz\\ & =\frac{\sigma }{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz\\ & =\frac{\sigma }{\sqrt{2\pi }}({\int }_{-\infty }^{0}z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz+{\int }_0^{\infty }z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz)\\ & =\frac{\sigma }{\sqrt{2\pi }}({\int }_{-\infty }^0(-t){\mathbf{e}}^{-\frac{1}{2}(-t{)}^2}d(-t)+{\int }_0^{\infty }z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz)\\ & =\frac{\sigma }{\sqrt{2\pi }}({\int }_{\infty }^{0}t{\mathbf{e}}^{-\frac{1}{2}{t}^2}dt+{\int }_0^{\infty }z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz)\\ & =\frac{\sigma }{\sqrt{2\pi }}(-{\int }_0^{\infty }t{\mathbf{e}}^{-\frac{1}{2}{t}^2}dt+{\int }_0^{\infty }z{\mathbf{e}}^{-\frac{1}{2}{z}^2}dz)\\ & =0\end{array}$$
第二个积分式其实就是正态分布的累积函数
$${\int }_{-\infty }^{\infty }\frac{\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx=\mu \cdot {\int }_{-\infty }^{\infty }\frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx=\mu \cdot 1$$
因此，
$$\begin{array}{rl}E(x)& ={\int }_{-\infty }^{\infty }\frac{x-\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx+{\int }_{-\infty }^{\infty }\frac{\mu }{\sigma }\cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\\ & =0+\mu \cdot 1\\ & =\mu \end{array}$$

正态分布的方差如下式所示。
$$\begin{array}{rl}Var(x)& ={\int }_{-\infty }^{\infty }(x-E(x){)}^{2}f(x)dx={\int }_{-\infty }^{\infty }(x-\mu {)}^2\cdot \frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\\ & ={\int }_{-\infty }^{\infty }(\frac{x-\mu }{\sigma }{)}^2\cdot \sigma \cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\end{array}$$
对上式使用变量变换$z=\frac{x-\mu }{\sigma }$
$$\begin{array}{rl}Var(x)& ={\int }_{-\infty }^{\infty }(\frac{x-\mu }{\sigma }{)}^2\cdot \sigma \cdot \frac{1}{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}dx\\ & ={\int }_{-\infty }^{\infty }{z}^2\cdot \frac{\sigma }{\sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}{z}^2}\sigma dz\\ & =\frac{{\sigma }^2}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{z}^2\cdot {\mathbf{e}}^{-\frac{1}{2}{z}^2}dz\end{array}$$
对上式使用变量变换$t=\frac{z}{\sqrt{2}}$
$$\begin{array}{rl}Var(x)& =\frac{{\sigma }^2}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{z}^2\cdot {\mathbf{e}}^{-\frac{1}{2}{z}^2}dz\\ & =\frac{{\sigma }^2}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }(\sqrt{2}t{)}^2\cdot {\mathbf{e}}^{-\frac{1}{2}(\sqrt{2}t{)}^2}d(\sqrt{2}t)\\ & =\frac{{\sigma }^2}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }2t^2\cdot {\mathbf{e}}^{-t^2}\cdot \sqrt{2}dt\\ & =\frac{2{\sigma }^2}{\sqrt{\pi }}{\int }_{-\infty }^{\infty }{t}^2\cdot {\mathbf{e}}^{-t^2}dt\\ & =\frac{2{\sigma }^2}{\sqrt{\pi }}{\int }_{-\infty }^{\infty }(-\frac{1}{2}t)\cdot d({\mathbf{e}}^{-t^2})\\ & =\frac{2{\sigma }^2}{\sqrt{\pi }}[(-\frac{1}{2}t)\cdot {\mathbf{e}}^{-t^2}{|}_{-\infty }^{+\infty }-{\int }_{-\infty }^{\infty }({\mathbf{e}}^{-t^2})\cdot d(-\frac{1}{2}t)]\end{array}$$
上式中第一项等于零，因为
$$\begin{gathered} \underset{t\to -\infty }{\lim }t\cdot {\mathbf{e}}^{-t^2}=\underset{t\to -\infty }{\lim }\frac{t}{{\mathbf{e}}^{t^2}}=0 \\ \underset{t\to +\infty }{\lim }t\cdot {\mathbf{e}}^{-t^2}=\underset{t\to +\infty }{\lim }\frac{t}{{\mathbf{e}}^{t^2}}=0 \end{gathered}$$
那么方差就只剩第二项了，这里要用到${\int }_{-\infty }^{\infty }{\mathbf{e}}^{-t^2}dt=\sqrt{\pi }$，这个方程可以从伽马函数中导出。
$$\begin{array}{rl}Var(x)& =\frac{2{\sigma }^2}{\sqrt{\pi }}\cdot \frac{1}{2}{\int }_{-\infty }^{\infty }{\mathbf{e}}^{-t^2}dt\\ & =\frac{{\sigma }^2}{\sqrt{\pi }}{\int }_{-\infty }^{\infty }{\mathbf{e}}^{-t^2}dt\\ & ={\sigma }^2\end{array}$$

2. 正态分布的代数运算

a. 单随机变量的代数运算

假设随机变量$X$服从正态分布，$X\sim N(\mu ,{\sigma }^2)$，那么随机变量$Y=aX+b$可由变量变换$X=\frac{Y-b}{a}$来导出，即随机变量$X$的累积函数为
$$\begin{array}{rl}F(x)& ={\int }_{-\infty }^{x}f(\xi )d\xi ={\int }_{-\infty }^x\frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(\xi -\mu {)}^2}{{\sigma }^2}}d\xi \\ & ={\int }_{-\infty }^{\frac{y-b}{a}}\frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(\frac{\eta -b}{a}-\mu {)}^2}{{\sigma }^2}}d(\frac{\eta -b}{a})\\ & ={\int }_{-\infty }^y\frac{1}{\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(\eta -b-a\mu {)}^2}{a^2{\sigma }^2}}\frac{1}{a}d\eta =F(y)\end{array}$$
那么随机变量$Y$的概率密度函数为
$$f(y)=\frac{dF(y)}{dy}=\frac{1}{a\sigma \sqrt{2\pi }}{\mathbf{e}}^{-\frac{1}{2}\frac{(\eta -b-a\mu {)}^2}{a^2{\sigma }^2}}$$
那么显然随机变量$Y$也是正态分布的，且$Y\sim N(b+a\mu ,a^2{\sigma }^2)$。

b. 两个正态分布随机变量的和

假设随机变量$X、Y$服从正态分布，$X\sim N({\mu }_X,{\sigma }_X^2)$，$Y\sim N({\mu }_Y,{\sigma }_Y^2)$，那么$Z=X+Y$服从什么分布呢？
我们从$Z$的累积函数定义出发观察，
$$F_Z(z)={\int }_{-\infty }^{z}f(Z)dZ$$
由$Z=X+Y$，那么$Z$的累积函数一定也可以表示成（X，Y）联合概率密度的积分形式，并且积分域如下图所示

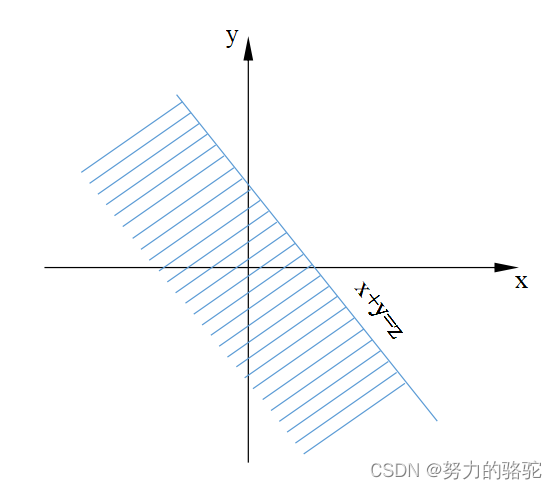
由二重积分的定义出发，我们可以得到
$$F_Z(z)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{z-x}f(x,y)dydx$$
用变量变换$y=\upsilon -x$，上式变成
$$\begin{array}{rl}{F}_Z(z)& ={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{z-x}f(x,y)dydx={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{z-x}f(x,\upsilon -x)d(\upsilon -x)dx\\ & ={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{z}f(x,\upsilon -x)d\upsilon dx\end{array}$$
那么随机变量$Z$的概率密度函数为
$$f_Z(z)=\frac{d{F}_Z(z)}{dz}={\int }_{-\infty }^{+\infty }f(x,z-x)dx$$
如果随机变量$X、Y$是独立的，那么
$$\begin{array}{rl}{f}_Z(z)& ={\int }_{-\infty }^{+\infty }f(x,z-x)dx={\int }_{-\infty }^{+\infty }{f}_X(x)f_Y(z-x)dx\\ & ={\int }_{-\infty }^{+\infty }\frac{1}{{\sigma }_x\sqrt{2\pi }}{\mathbf{e}}^{-\frac{(x-{\mu }_x{)}^2}{2{\sigma }_x^2}}\frac{1}{{\sigma }_y\sqrt{2\pi }}{\mathbf{e}}^{-\frac{(z-x-{\mu }_y{)}^2}{2{\sigma }_y^2}}dx\\ & ={\int }_{-\infty }^{+\infty }\frac{1}{{\sigma }_x{\sigma }_{y}2\pi }{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}-\frac{1}{2}(\sqrt{\frac{{\sigma }_x^2+{\sigma }_y^2}{{\sigma }_x^2\cdot {\sigma }_y^2}}x+\frac{{\sigma }_{x}z}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_y{\mu }_x}{{\sigma }_x\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_x{\mu }_y}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}{)}^2}dx\\ & =\frac{1}{{\sigma }_x{\sigma }_{y}2\pi }{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}{\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}(\sqrt{\frac{{\sigma }_x^2+{\sigma }_y^2}{{\sigma }_x^2\cdot {\sigma }_y^2}}x+\frac{{\sigma }_{x}z}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_y{\mu }_x}{{\sigma }_x\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_x{\mu }_y}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}{)}^2}dx\\ & =\frac{1}{{\sigma }_x{\sigma }_{y}2\pi }{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}\sqrt{\frac{{\sigma }_x^2\cdot {\sigma }_y^2}{{\sigma }_x^2+{\sigma }_y^2}}{\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}(\sqrt{\frac{{\sigma }_x^2+{\sigma }_y^2}{{\sigma }_x^2\cdot {\sigma }_y^2}}x+\frac{{\sigma }_{x}z}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_y{\mu }_x}{{\sigma }_x\sqrt{{\sigma }_x^2+{\sigma }_y^2}}+\frac{{\sigma }_x{\mu }_y}{{\sigma }_y\sqrt{{\sigma }_x^2+{\sigma }_y^2}}{)}^2}d(\sqrt{\frac{{\sigma }_x^2+{\sigma }_y^2}{{\sigma }_x^2\cdot {\sigma }_y^2}}x)\\ & =\frac{1}{2\pi \sqrt{{\sigma }_x^2+{\sigma }_y^2}}{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}{\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}{t}^2}dt\end{array}$$
这其中
$${\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}{t}^2}dt=\sqrt{2}\cdot {\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}{t}^2}d(\frac{t}{\sqrt{2}})=\sqrt{2}\cdot {\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-{\tau }^2}d\tau =\sqrt{2}\cdot \sqrt{\pi }$$
那么
$$\begin{array}{rl}{f}_Z(z)& =\frac{1}{2\pi \sqrt{{\sigma }_x^2+{\sigma }_y^2}}{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}{\int }_{-\infty }^{+\infty }{\mathbf{e}}^{-\frac{1}{2}{t}^2}dt\\ & =\frac{1}{2\pi \sqrt{{\sigma }_x^2+{\sigma }_y^2}}{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}\sqrt{2}\cdot \sqrt{\pi }\\ & =\frac{1}{\sqrt{2\pi }\sqrt{{\sigma }_x^2+{\sigma }_y^2}}{\mathbf{e}}^{-\frac{(z-{\mu }_x-{\mu }_y{)}^2}{2({\sigma }_x^2+{\sigma }_y^2)}}\end{array}$$
不难得出随机变量$Z$也是服从正态分布，并且$Z\sim N({\mu }_X+{\mu }_Y,{\sigma }_X^2+{\sigma }_Y^2)$。

c. 多个正态分布随机变量的线性组合

假设随机变量$X_1、X_2、...、X_n$服从正态分布，$X_i\sim N({\mu }_i,{\sigma }_i^2)$，那么$Z=\sum a_i{X}_i$服从什么分布呢？
通过a节、b节内容，不难得出随机变量$Z$服从正态分布，且$Z\sim N(\sum a_i{\mu }_i,\sum a_i^2{\sigma }_i^2)$。