基本操作



树的相关定义
树的深度(高度):树中叶子结点所在的最大层次
森林: m m m棵互不相交的树的集合
二叉树
二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、互不交的二叉树组成。
性质
- 二叉树,第
i
i
i层上至多有
2
i
−
1
2^{i-1}
2i−1的结点(
i
≥
1
i≥1
i≥1)
这个性质比较好理解,因为第i层是由i-1层引出的,再以此递归到根结点就很好理解 - 深度为
k
k
k 的二叉树上至多含
2
k
−
1
2^k-1
2k−1 个结点(
k
≥
1
k≥1
k≥1)
这个也很好理解,先把树想象成一棵满二叉树,因为根结点那层只有一个结点,所以减一即可 - 对任何一棵二叉树,若它含有 n 0 n_0 n0个叶子结点、 n 2 n_2 n2 个度为 2 2 2 的结点,则必存在关系式: n 0 = n 2 + 1 n_0 = n_2+1 n0=n2+1
- 具有 n 个结点的完全二叉树的深度为
l
o
g
2
n
+
1
log_2n+1
log2n+1
用第2条性质很好理解 - 对于含有
n
n
n 个节点的完全二叉树,我们可以按照从上到下、从左到右的顺序为每个节点进行编号,从
1
1
1 到
n
n
n。对于任意一个编号为
i
i
i 的节点:
- 如果 i = 1 i=1 i=1 ,那么该节点就是整棵二叉树的根节点,它没有父节点;否则,它的父节点的编号为 ⌊ i / 2 ⌋ \lfloor i/2 \rfloor ⌊i/2⌋。
- 如果 2 i > n 2i>n 2i>n,那么编号为 i i i 的节点没有左孩子,否则,它的左孩子的编号为 2 i 2i 2i。
- 如果 2 i + 1 > n 2i+1>n 2i+1>n,那么编号为 i i i 的节点没有右孩子,否则,它的右孩子的编号为 2 i + 1 2i+1 2i+1。
这些规则的推论可以帮助我们更好地理解完全二叉树的结构,而且可以方便地进行完全二叉树节点的查找和遍历。
完全二叉树:
完全二叉树是一种特殊的二叉树,它与普通的二叉树区别在于它的层数,及对于第 i i i 层,如果该层的节点没有填满,则其所有节点都必须集中在左侧连续位置上。也就是说,完全二叉树中除最后一层外,其他层的节点数都达到了最大值,且最后一层的节点都集中在该层最左边的若干位置上。
存储结构
顺序存储
#define MAX_TREE_SIZE 100 // 二叉树的最大结点数
typedef int TElemType; // 定义元素类型为整型
typedef struct BiTNode {
TElemType data; // 数据域
struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTNode, *BiTree; // 二叉链表结点定义和二叉树定义
BiTree bt; // 定义一个指向二叉树根节点的指针
二叉链表
// 定义二叉树结点和指向二叉树结点的指针类型
typedef struct BiTNode {
TElemType data; // 数据域
struct BiTNode *lchild, *rchild; // 左右孩子指针
} BiTNode, *BiTree;
示意图
| lchild | data | rchild |
|---|
三叉链表
// 定义三叉链表结点和指向三叉链表结点的指针类型
typedef struct TriTNode {
TElemType data; // 数据域
struct TriTNode *lchild, *rchild; // 左右孩子指针
struct TriTNode *parent; // 双亲指针
} TriTNode, *TriTree;
根节点的 p a r e n t parent parent为NULL
| parent | lchild | data | rchild |
|---|
二叉树遍历
- 先序遍历
根左右 - 中序遍历
左根右 - 后序遍历
左右根
先序遍历算法比较简单,我就不放了
中序遍历:
//采用非递归的方式,中序遍历以T为根指针的二叉树
Status InOrderTraverse(BiTree T, Status (*Visit)(TElemType e)){
SqStack S; //定义一个栈 S 来存储节点。
InitStack(&S); //初始化栈
BiTree p = T; //p为遍历指针,初始时指向根结点
while (p || !StackEmpty(S)){ //p非空或者栈不为空
if (p){ //如果p非空
Push(&S, p); //节点入栈
p = p->lchild; //遍历左子树
}
else{ //如果p为空
Pop(&S, &p); //取出栈顶元素
if (!Visit(p->data)) return ERROR; //访问栈顶元素
p = p->rchild; //遍历右子树
}
}
return OK;
}
创建二叉树
//按照前序遍历方式,创建一棵二叉树,并返回 OK
Status CreateBiTree(BiTree &T) {
char ch; //定义一个字符类型的变量 ch 用于输入二叉树结点的值
scanf("%c", &ch); //从用户输入中读取下一个字符,即当前结点的值
if (ch == ' ') T = NULL; //如果输入的是空格,则表示该结点为空结点
else { //否则,生成一个新的二叉树结点,并赋值为 ch
if (!(T = (BiTNode *)malloc(sizeof(BiTNode))))
exit(OVERFLOW); //若生成结点失败,则退出程序
T->data = ch; //为当前结点赋值
CreateBiTree(T->lchild); //递归调用 CreateBiTree 函数构造左子树
CreateBiTree(T->rchild); //递归调用 CreateBiTree 函数构造右子树
}
return OK; //返回 OK 表示创建成功
}
由先序和中序遍历构建二叉树:
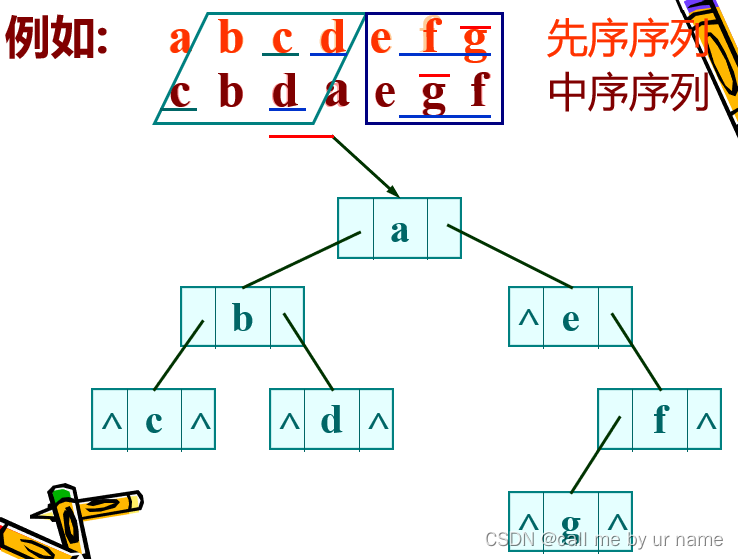
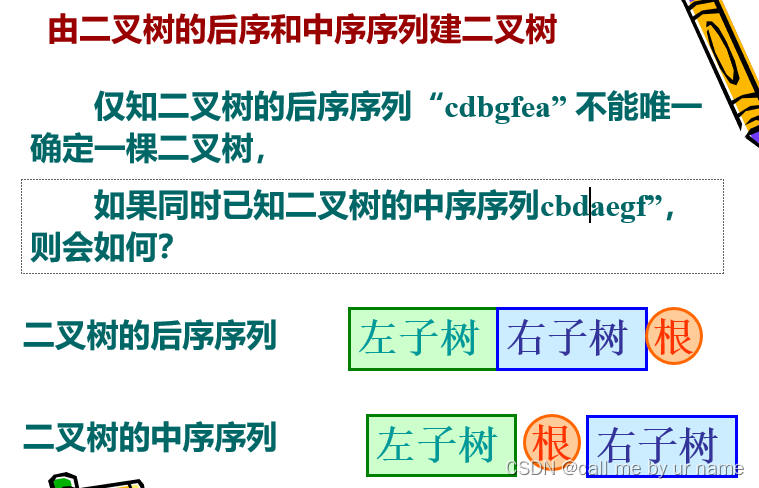
由后序和中序构建:
线索二叉树
线索二叉树是在二叉树的基础上增加了线索信息的一种数据结构。线索二叉树的每个结点除了指向左右子树的指针外,还有两个特殊指针,分别称为前驱线索和后继线索指针,用来记录该结点在中序遍历中的前驱和后继结点。
在线索二叉树中,如果一个结点没有左子树,则将其左子树指针指向该结点在中序遍历中的前驱结点;如果一个结点没有右子树,则将其右子树指针指向该结点在中序遍历中的后继结点。当然并非一定中序遍历,只是书上的内容多是中序遍历
线索化过程即为将二叉树转换成线索二叉树的过程。线索化的方法主要有以下两种:
- 中序遍历线索化:对于给定的二叉树,中序遍历得到的结点序列中,每个结点都有唯一的前驱和后继。通过修改二叉树中的指针,使其变成一个线性的结构,同时保留原有的中序遍历序列,即可得到该二叉树的线索二叉树。
- 先序遍历线索化:与中序遍历类似,只是遍历顺序不同。
线索二叉树的主要优点是可以加快对二叉树的遍历操作,同时节省存储空间。缺点是线索化过程需要额外的时间开销,并且增加了代码的复杂度。
typedef enum { Link, Thread } PointerThr; // Link==0:指针,Thread==1:线索
typedef struct BiThrNode {
TElemType data; // 结点数据
struct BiThrNode *lchild; // 左子树指针
struct BiThrNode *rchild; // 右子树指针
PointerThr LTag; // 左标志
PointerThr RTag; // 右标志
} BiThrNode, *BiThrTree;
遍历算法
void InOrderTraverse_Thr(BiThrTree T, void (*Visit)(TElemType e)) {
BiThrTree p = T->lchild; // p指向根结点的左子树
while (p != T) { // 空树或遍历结束时,p==T
while (p->LTag == Link) p = p->lchild; // 如果左标志为指针,则p进至其左子树的最左下结点
if (!Visit(p->data)) return; // 访问该结点,如果访问失败则返回错误
while (p->RTag == Thread && p->rchild != T) {
p = p->rchild; Visit(p->data); // 循环访问后继结点,直到遇到右标志为指针的结点
}
p = p->rchild; // 如果右标志为指针,则p进至其右子树的根结点
}
}
仔细看看吧,第一次看的时候还有点不理解
建立线索链表
Status InOrderThreading(BiThrTree &Thrt, BiThrTree T) {
if (!T) { // 如果二叉树为空,则创建头结点并将左右指针都指向自身
if (!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) {
exit(OVERFLOW);
}
Thrt->LTag = Link;
Thrt->RTag = Thread;
Thrt->lchild = Thrt;
Thrt->rchild = Thrt;
return OK;
}
// 否则,创建头结点,并将左指针指向根节点,右指针指向尾节点
if (!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) {
exit(OVERFLOW);
}
Thrt->LTag = Link;
Thrt->RTag = Thread;
Thrt->rchild = Thrt;
pre = Thrt; // 初始化前驱节点,方便遍历时标记前驱线索
Thrt->lchild = T; // 左指针指向根节点
InThreading(T); // 中序遍历二叉树并进行线索化
pre->rchild = Thrt; // 将最后一个节点的右子树指针指向头结点
pre->RTag = Thread;
Thrt->rchild = pre; // 将头结点的右指针指向最后一个节点
return OK;
}
首先判断输入的二叉树是否为空。如果为空,则创建一个头结点,并将左右指针都指向自身。否则,我们创建一个头结点,将其左指针指向根节点,将其右指针指向尾节点。
接下来,我们初始化前驱节点 pre,并将其指向头结点,以便遍历二叉树时能够方便地标记前驱线索。然后,我们将头结点的左指针指向根节点,调用函数 InThreading 对二叉树进行中序线索化。
在 InThreading 函数返回后,我们需要找到最后一个节点,并将它的右子树指针指向头结点。我们使用变量 pre 来保存当前遍历过的最后一个节点,在循环中不断更新,直到遍历到最后一个节点。最后,我们将最后一个节点的右子树指针指向头结点,并将头结点的右指针指向最后一个节点。
需要注意的是,在整个过程中,我们只需要通过修改线索来实现中序遍历,无需创建新的节点或者修改原有节点的结构。这就是中序线索二叉树的优点,它可以大大提高中序遍历的效率,减少程序的内存占用。
这个算法的具体实现还是有点复杂的
In Threading函数
void InThreading(BiThrTree p, BiThrTree &pre) {
if (!p) { // 如果当前节点为空,则直接返回
return;
}
// 对左子树进行线索化
InThreading(p->lchild, pre);
// 建立前驱线索
if (!p->lchild) {
p->LTag = Thread;
p->lchild = pre;
}
// 建立后继线索
if (pre && !pre->rchild) {
pre->RTag = Thread;
pre->rchild = p;
}
pre = p; // 确定当前节点的前驱节点
// 对右子树进行线索化
InThreading(p->rchild, pre);
}
森林与树
表示法
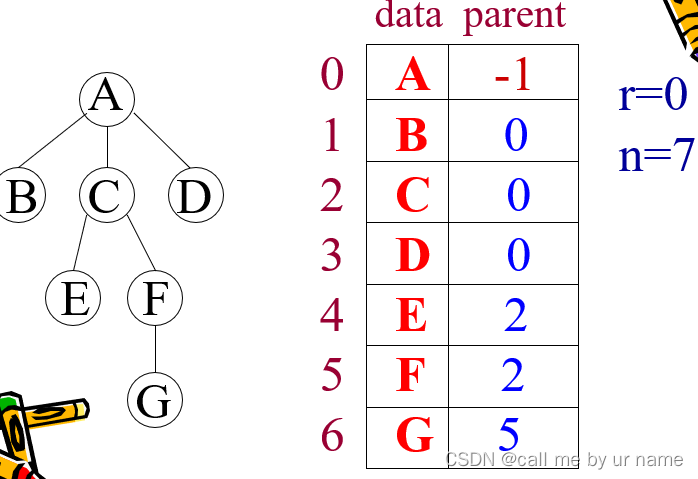
双亲表示法
孩子链表表示法
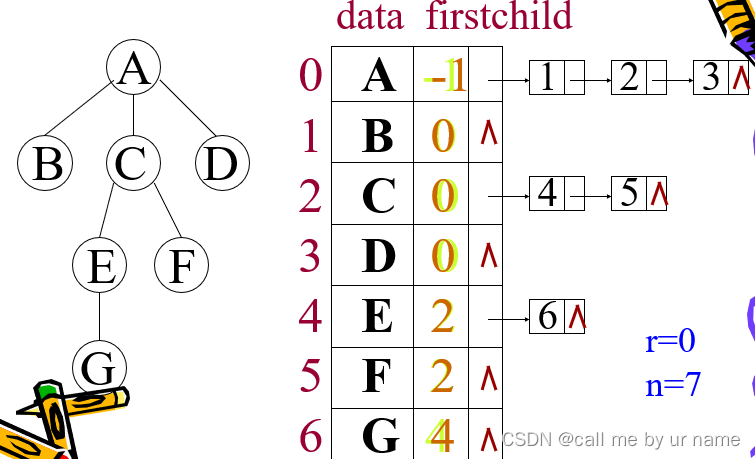
比双亲表示法多了一个存储孩子的域空间
树的二叉链表(孩子-兄弟)表示法
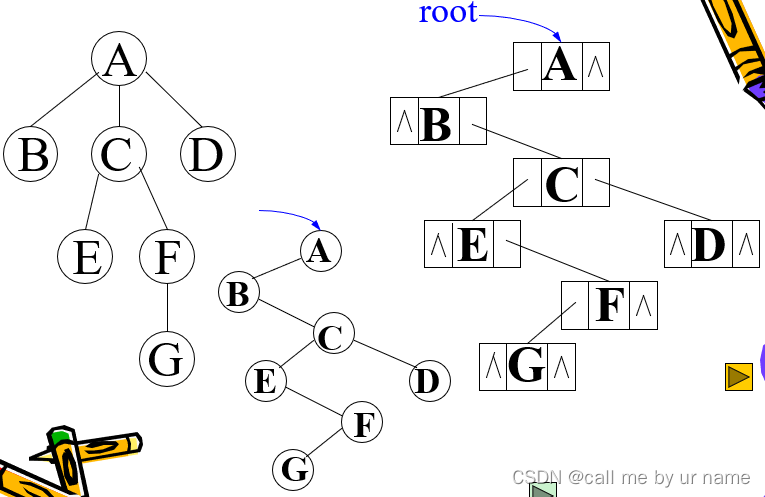
左孩子-右兄弟
二叉树与森林的转换
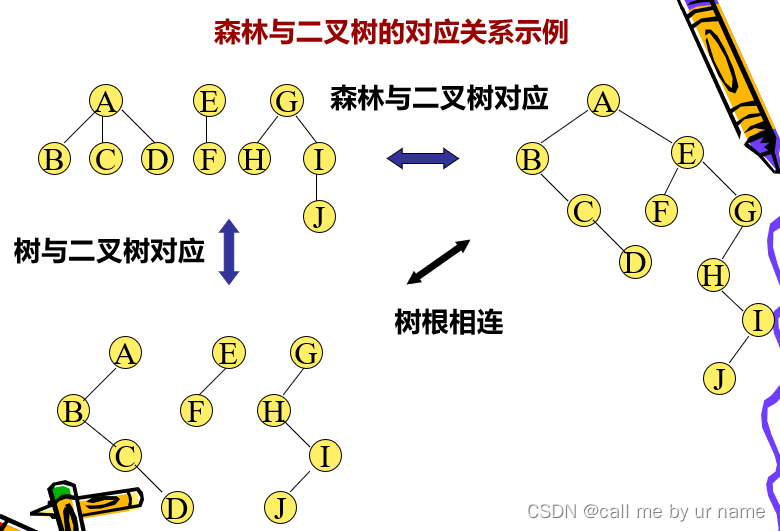
遍历
树的遍历:
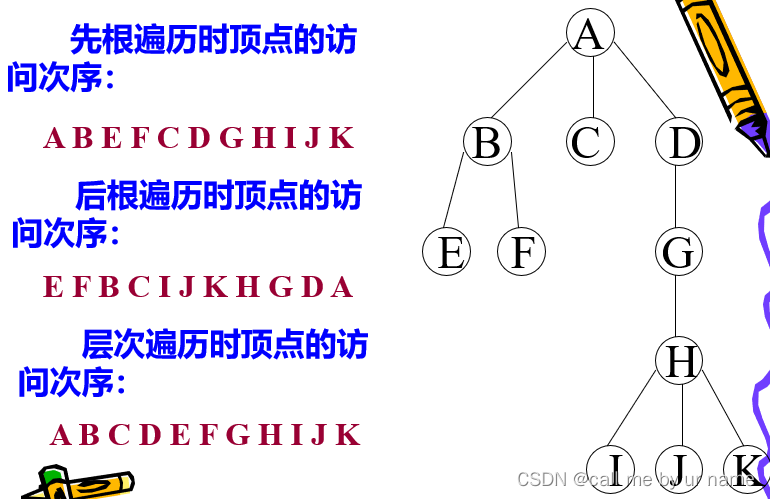
层次遍历——BFS
森林的遍历:
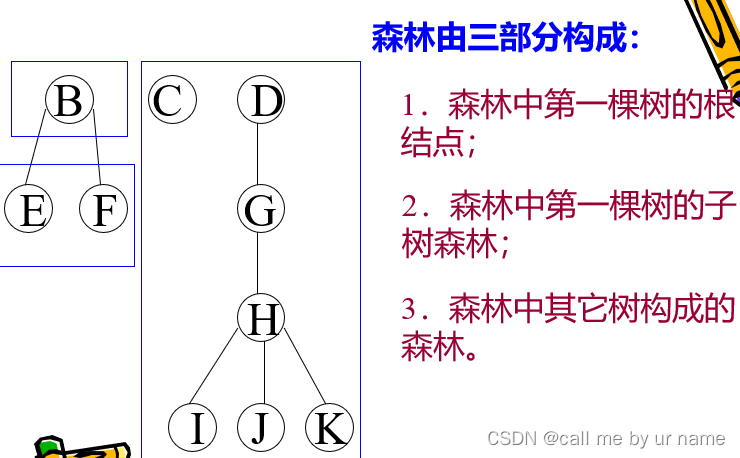
-
若森林不空,则可按下述规则遍历之:(先序遍历)
(1)访问森林中第一棵树的根结点;
(2)先序遍历森林中第一棵树的子树森林;
(3)先序遍历森林中(除第一棵树之外)其余树构成的森林。 -
若森林不空,则可按下述规则遍历之:(中序遍历)
(1)中序遍历森林中第一棵树的子树森林;
(2)访问森林中第一棵树的根结点;
(3)中序遍历森林中(除第一棵树之外)其余树构成的森林。

树的存储结构
typedef struct CSNode {
Elem data;
struct CSNode *left, *right; // 左儿子和右兄弟指针
} CSNode, *CSTree;
左孩子-右兄弟
常见应用算法
求树的深度
int TreeDepth(CSTree T) {
if (!T) {
return 0;
} else {
int h1 = TreeDepth(T->left); // 递归求左子树深度
int h2 = TreeDepth(T->right); // 递归求右子树深度
return (h1 > h2 ? h1 : h2) + 1; // 返回深度较大的子树深度加1
}
} // TreeDepth
求从根到所有叶子的路径
void AllPath(Bitree T, Stack &S) {
if (T) {
Push(S, T->data);
if (!T->left && !T->right) {
PrintStack(S);
} else {
AllPath(T->left, S);
AllPath(T->right, S);
}
Pop(S);
}
} // AllPath
Huffman
结点的路径长度:
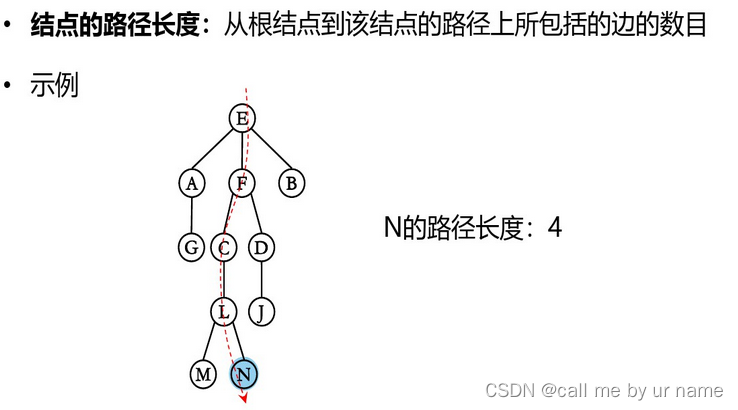
树的路径长度:从树根到每个结点的路径长度之和
结点的带权路径长度:从该结点到树根之间的路径长度与结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。记作: WPL(T) = ∑wklk (对所有叶子结点)。
构造最优二叉树的一种算法——huffman算法
霍夫曼算法的实现过程如下:
- 计算每个字符在文本中出现的频率;
- 将所有字符和其频率作为叶子节点构建一棵二叉树,其中节点的权重值为该节点代表的字符的频率;
- 对于这棵二叉树,从中选择两个权重值最小的节点作为左右子树,将它们的权重值相加并作为新节点的权重值;
- 将这个新节点作为子树的根节点,并将它插入到二叉树中原来两个被选中的节点所在的位置;
- 重复步骤 3 和 4 直到整棵树变成一个节点,这个节点就是霍夫曼树的根节点;
- 对于每个字符,从根节点开始,如果字符在左子树中,则输出0,否则输出1,直到找到对应的叶子节点;
- 将所有字符的编码串连接起来,就是压缩后的数据。
huffman结构体
typedef struct {
unsigned int weight;
unsigned int parent;
unsigned int lchild;
unsigned int rchild;
} HTNode, *HuffmanTree;
huffman编码
void HuffmanCoding(HuffmanTree& HT, HuffmanCode& HC, int* w, int n) {
// w 存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HC。
if (n <= 1) return;
int m = 2 * n - 1; // 计算哈夫曼树节点数
HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode)); // 动态分配内存
// 初始化叶子节点
for (int i = 1; i <= n; ++i) {
HT[i].weight = w[i-1];
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
// 初始化内部节点
for (int i = n+1; i <= m; ++i) {
HT[i].weight = 0;
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
// 建立哈夫曼树
for (int i = n+1; i <= m; ++i) {
// 在HT[1..i-1]选择parent为0且weight最小的两个结点,其序号分别为s1和s2。
Select(HT, i-1, s1, s2);
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
// 分配编码头指针向量
HC = (HuffmanCode)malloc((n+1) * sizeof(char*));
// 分配求编码的工作空间
cd = (char*)malloc(n * sizeof(char));
cd[n-1] = '\0'; // 编码结束符
// 逐个字符求编码并保存到HC中
for (int i = 1; i <= n; ++i) {
int start = n-1; // 编码结束符位置
int c = i, f = HT[i].parent;
// 从叶子到根逆向求编码
while (f != 0) {
if (HT[f].lchild == c) {
cd[--start] = '0';
}
else {
cd[--start] = '1';
}
c = f;
f = HT[f].parent;
}
HC[i] = (char*)malloc((n-start) * sizeof(char));
// 为第i个字符编码分配空间
strcpy(HC[i], &cd[start]); // 从 cd 复制编码串到 HC
}
free(cd); //释放工作空间
}
这个有点复杂,其中编码部分可以用更好理解的递归来解决
void generateHuffmanCodes(HuffmanNode* root, string code) {
if (!root) return;
if (root->left == nullptr && root->right == nullptr) codes[root->ch] = code;
generateHuffmanCodes(root->left, code + "0");
generateHuffmanCodes(root->right, code + "1");
}
习题
相似
若已知两棵二叉树
B
1
B1
B1
B
2
B2
B2 皆为空,或者皆不空且
B
1
B1
B1 的左、右子树和
B
2
B2
B2的左、右子树分别相似,则称二叉树
B
1
B1
B1和
B
2
B2
B2 相似。试编写算法,判别给定两棵二叉树是否相似。

比较简单,但不妨看看
栈实现后序遍历
写出后序遍历的非递归算法(提示:为分辨后序遍历时两次进栈的不同返回点,需在指针进栈时同时将一个标志进栈)。

仔细看看
层次遍历
编写按层次顺序(同一层自左至右)遍历二又树的算法。

判断完全二叉树
bool full(tree t) {
init_queue(q);
int flag = 0;
enqueue(q, t);
while (!queue_empty(q)) {
dequeue(q.p);
if (!p) {
flag = 1;
} else if (flag) {
return 0;
} else {
enqueue(q, p->lchild);
enqueue(q, p->rchild);
}
}
return 1;
}
求孩子-兄弟链的深度
typedef struct TreeNode * Tree;
int depth(Tree root) {
if (!root) {
return 0; // 如果节点为空,深度为 0
}
int maxDepth = 0;
for (Tree p = root->firstChild; p; p = p->rightSibling) {
int d = depth(p); // 递归计算子节点的深度
if (d > maxDepth) {
maxDepth = d; // 记录最大深度
}
}
return maxDepth + 1; // 当前节点的深度等于最深子节点的深度加上 1
}
Tree p = root->firstChild; p; p = p->rightSibling
这一条代码可以好好看看
依据前序序列和中序序列构建二叉树(二叉链表)
Tree buildTree(int preorder[], int inorder[], int n) {
if (n == 0) {
return NULL; // 当序列为空时,返回空指针
}
// 在前序序列中找到根节点
int root_val = preorder[0];
int i;
for (i = 0; i < n; i++) {
if (inorder[i] == root_val) {
break;
}
}
// 根据中序序列划分左右子树
int left_size = i;
int right_size = n - i - 1;
// 递归构建左右子树
Tree root = (Tree) malloc(sizeof(struct TreeNode));
root->val = root_val;
root->left = buildTree(preorder + 1, inorder, left_size);
root->right = buildTree(preorder + 1 + left_size, inorder + 1 + left_size, right_size);
return root;
}
依据递归解决即可