系列文章目录

前言

        本文主要介绍BIRCH算法、DBSCAN算法、OPTICS算法，以及相关案例举例，以下案例仅供参考

一、BIRCH算法

1.1、BIRCH算法简介

        BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies，平衡迭代规约和层次聚类）是一种基于树结构的聚类算法，其主要思想是使用一棵 CF 树（Clustering Feature Tree，聚类特征树）来表示数据集，通过不断对 CF 树进行迭代规约和层次聚类来实现对数据集的聚类。该算法具有高效性和可扩展性，并且可以处理大数据集。

在 Python 中，scikit-learn 库提供了 BIRCH 的实现，可以使用 `sklearn.cluster.Birch` 类来进行聚类。该类的主要参数包括：

• - `threshold`: float, optional (default=0.5)，叶子节点的阈值，用于控制 CF 树的大小，默认值为 0.5。
• - `branching_factor`: int, optional (default=50)，分支因子，用于控制 CF 树的分支度，默认值为 50。
• - `n_clusters`: int or None，聚类的数量，默认为 None，表示不指定聚类的数量，而是通过阈值和分支因子来自动确定聚类的数量。

在 `Birch` 类中，有以下常用的方法：

• - `fit(X[, y])`: 对数据 X 进行聚类，并返回一个 `Birch` 对象。
• - `fit_predict(X[, y])`: 对数据 X 进行聚类，并返回每个数据点的簇标签。
• - `predict(X)`: 对新数据 X 进行预测，返回每个数据点的簇标签。
• - `transform(X)`: 将数据 X 转换成 CF 树中的叶子节点，返回一个稀疏矩阵。

除此之外，还有一些其他的参数和方法，可以根据具体需求来使用。

1.2、案例举例

案例

#使用BIRCH算法进行聚类
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.cluster import Birch
from itertools import cycle
N1,N2=500,500#样本数量
from sklearn.datasets import make_classification


X,labels = make_classification(n_samples = N1+N2,n_features = 2,n_redundant = 0,n_clusters_per_class = 1)
for class_value in range(2):
    row_ix = np.where(labels == class_value)
    plt.scatter(X[row_ix,0],X[row_ix,1],color = 'k',marker = 'o',s=5)
    plt.title("初始数据发布")
plt.xlabel("属性1")
plt.ylabel("属性2")
plt.show()
#也可以使用生成的正态分布随机数的方法生成数据
mu1,cov1 = [0,0],[[1,0],[0,2]]
set1 = np.random.multivariate_normal(mu1,cov1,N1)
mu2,cov2 = [5,5],[[1,0.9],[0.9,1]]
set2 = np.random.multivariate_normal(mu2,cov2,N2)
X=np.vstack([set1,set2])
fig = plt.figure()
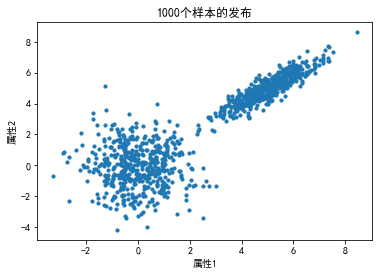
plt.scatter(X[:,0],X[:,1],s=10)
plt.title("%d个样本的发布"%(N1+N2))
plt.xlabel("属性1")
plt.ylabel("属性2")
plt.show()
B,T=[100,150,200],[1,1.5,2]
i=1
colors=cycle('bgrcmyk')
for b,tau in zip(B,T):
    plt.figure()
    bir = Birch(n_clusters=None,threshold = tau,branching_factor = b)
    bir.fit(X)
    labels=np.unique(bir.labels_)
    print('标签的个数：',len(labels))
    print(bir.root_)
    i+=1
    for color,k in zip(colors,labels):
        plt.scatter(X[bir.labels_==k,0],X[bir.labels_==k,1],c=color,s=10,alpha = 0.5)
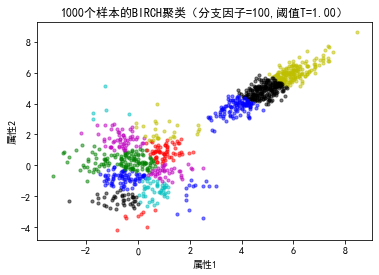
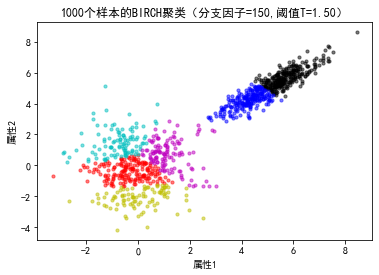
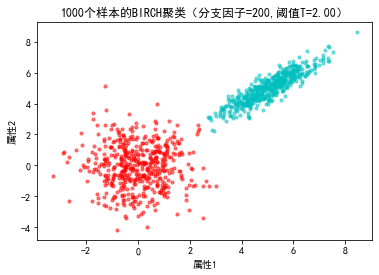
    plt.title("%d个样本的BIRCH聚类（分支因子=%d,阈值T=%.2f）"%(N1+N2,b,tau))
    plt.xlabel("属性1")
    plt.ylabel("属性2")
    plt.show()

标签的个数： 15
<sklearn.cluster._birch._CFNode object at 0x0000022BA0E6B9D0>

标签的个数： 6
<sklearn.cluster._birch._CFNode object at 0x0000022BA0CD56A0>

标签的个数： 2
<sklearn.cluster._birch._CFNode object at 0x0000022BA0E08CA0>

from sklearn.cluster import Birch
B,T=[100,150,200],[1, 1.5,2]
i=1
#定义分支因子和阈值的组合
#BIRCH聚类结果数量未知，所以作图时用cyclc控制颜色循环 
from itertools import cycle 
colors = cycle('bgrcmyk')
for b,tau in zip(B,T):
    plt.figure() 
    bir = Birch(n_clusters=None,threshold=tau,branching_factor=b) 
    bir.fit(X)
    labels =np.unique(bir.labels_)
    i+=1 
    for color,k in zip(colors,labels):
        plt.scatter(X[bir.labels_==k,0],X[bir.labels_==k,1],c=color)
    plt.show()

运行结果：

二、DBSCAN算法

2.1、算法简介

        DBSCAN 是一种基于密度的聚类算法，它的主要思想是将高密度的数据点聚成一类，低密度的数据点视为噪声或离群点。在 DBSCAN 中，密度被定义为在某个半径范围内的数据点个数。具体来说，该算法需要指定两个参数：半径 ε 和最小邻居数 minPts。对于某个数据点，如果它的 ε-邻域（即距离该点不超过 ε 的所有点）中包含不少于 minPts 个数据点，则该点被视为一个核心点；如果某个数据点在某个核心点的 ε-邻域中，但它自身不是核心点，则该点被视为边界点；如果某个数据点的 ε-邻域中没有包含不少于 minPts 个数据点，则该点被视为噪声或离群点。通过以上定义，DBSCAN 可以将数据点分成三类：核心点、边界点和噪声点。该算法的优点是可以处理任意形状的簇，并且可以有效地过滤噪声和离群点。

        DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，其基本思想是将高密度的数据点聚成一类，低密度的数据点视为噪声或离群点。该算法可以处理任意形状的簇，并且可以有效地过滤噪声和离群点。

         DBSCAN算法中的参数包括eps和min_samples。eps参数指定了一个点的邻域半径，min_samples指定了在eps半径内最少需要有多少个点才能形成一个簇。除此之外，还有一个可选参数metric，表示使用哪种距离度量来计算点之间的距离，默认值为欧几里得距离。

        在Python中，可以使用scikit-learn库中的sklearn.cluster.DBSCAN类来进行DBSCAN聚类，并可以根据具体需求设置参数和使用方法。DBSCAN类的主要方法包括fit和predict，其中fit方法用于训练模型，predict方法用于预测样本所属的簇标签。

以下是一些常用的参数和函数说明：

• - eps: float, default=0.5 最大距离
• - min_samples: int, default=5 最小样本数
• - metric: string, callable or None, default='euclidean' 距离度量，默认为欧几里得距离 
• - fit(X[, y, sample_weight])：进行模型训练
• - fit_predict(X[, y, sample_weight])：进行模型训练并返回聚类标签
• - labels_：返回聚类标签
• - core_sample_indices_：返回核心样本的索引
• - components_：返回每个簇的质心

2.2、案例举例

案例1：

#使用DBSCAN算法实现聚类
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.datasets import make_moons
from sklearn.datasets import make_circles
from sklearn import cluster
noises = [0.05,0.1,0.15]
for noise in noises:
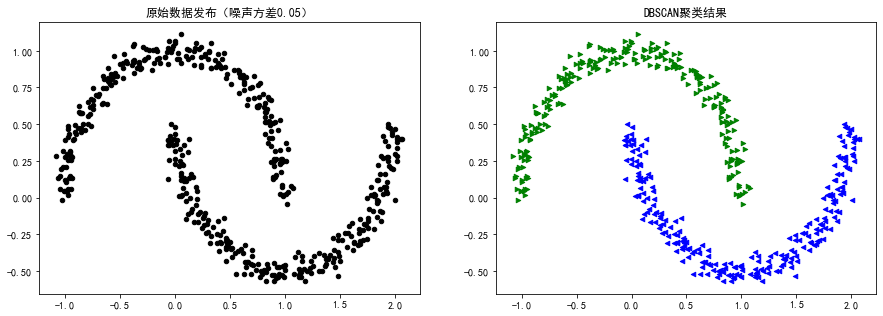
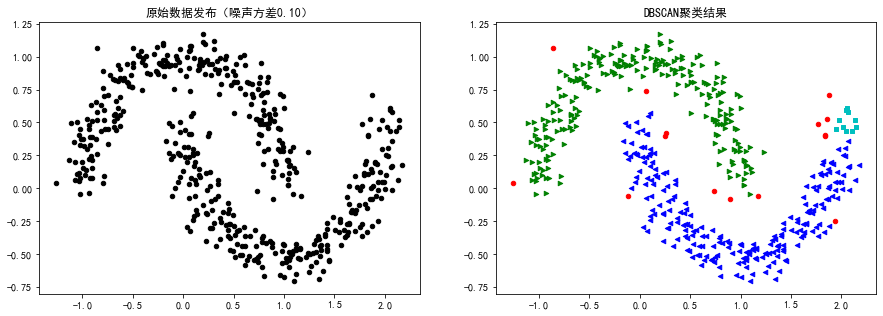
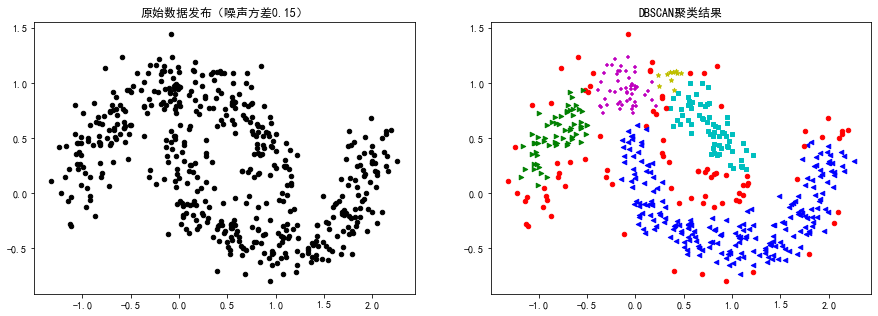
    X,labels = make_moons(n_samples = 500,noise = noise)
    plt.figure(figsize=(15,5))
    plt.subplot(121)
    plt.scatter(X[:,0],X[:,1],color = "black",s=20)
    plt.title("原始数据发布（噪声方差%.2f）"%noise)
    
    db = cluster.DBSCAN(eps = 0.15,min_samples = 10)
    db.fit(X)
    print('DBSCAN算法参数：',db.get_params())
    result = np.unique(db.labels_)
    print('DBSCAN类别标签：',result)
    plt.subplot(122)
    colors = ["b","g","c","m","y","k","r"]
    markers = ["<",">","s","+","*","^","o"]
    labels = ['簇1','簇2','簇3','簇4','簇5','簇6','噪声']
    for i,j in enumerate(db.labels_):
        plt.scatter(X[i][0],X[i][1],color = colors[j],marker = markers[j],s = 20)
    plt.title("DBSCAN聚类结果")
    plt.show()

运行结果：

DBSCAN算法参数： {'algorithm': 'auto', 'eps': 0.15, 'leaf_size': 30, 'metric': 'euclidean', 'metric_params': None, 'min_samples': 10, 'n_jobs': None, 'p': None}
DBSCAN类别标签： [0 1]

DBSCAN算法参数： {'algorithm': 'auto', 'eps': 0.15, 'leaf_size': 30, 'metric': 'euclidean', 'metric_params': None, 'min_samples': 10, 'n_jobs': None, 'p': None}
DBSCAN类别标签： [-1  0  1  2]

DBSCAN算法参数： {'algorithm': 'auto', 'eps': 0.15, 'leaf_size': 30, 'metric': 'euclidean', 'metric_params': None, 'min_samples': 10, 'n_jobs': None, 'p': None}
DBSCAN类别标签： [-1  0  1  2  3  4]

案例2：

import numpy as np
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
%matplotlib inline

# 生成样本数据
X, y = make_blobs(n_samples=500, centers=5, random_state=42)

# 对数据进行标准化
X = StandardScaler().fit_transform(X)

# 创建 DBSCAN 对象并进行聚类
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan.fit(X)

# 绘制聚类结果
plt.scatter(X[:,0], X[:,1], c=dbscan.labels_, cmap='rainbow')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

运行结果：

 

三、OPTICS算法

3.1、算法简介

OPTICS是一种基于密度的聚类算法，可以有效地识别具有不同密度的数据簇。与DBSCAN不同，OPTICS不需要事先知道簇的数量。它通过在数据集中生成一个基于密度的可达性图来工作，从而可以在处理具有任意形状的簇时表现出良好的性能。

在Python中，可以使用scikit-learn库中的`sklearn.cluster.OPTICS`类来实现OPTICS聚类。该类的主要参数和函数如下：

**主要参数：**

• - `min_samples`: 用于定义一个数据点的邻域中必须包含的最少数据点数。默认值为5。
• - `xi`: 用于控制点之间的相似度度量。默认值为0.05。
• - `min_cluster_size`: 用于定义簇的最小数量。默认值为None（自适应）。
• - `max_eps`: 用于定义一个点的邻域的最大半径。默认值为inf。

**主要函数：**

• - `fit(X)`: 对数据集X进行聚类，并返回OPTICS聚类器对象。
• - `fit_predict(X)`: 对数据集X进行聚类，并返回聚类标签。
• - `set_params(**params)`: 设置OPTICS聚类器的参数。
• - `get_params()`: 获取OPTICS聚类器的参数。

需要注意的是，由于OPTICS算法的计算复杂度较高，因此在处理大数据集时可能会遇到效率问题。在这种情况下，可以考虑使用DBSCAN或BIRCH等其他聚类算法来代替。

3.2、案例举例

案例1：

#使用OPTICS算法实现聚类
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.datasets import make_moons
from sklearn.datasets import make_circles
from sklearn import cluster
noises = [0.05,0.1,0.15]
for noise in noises:
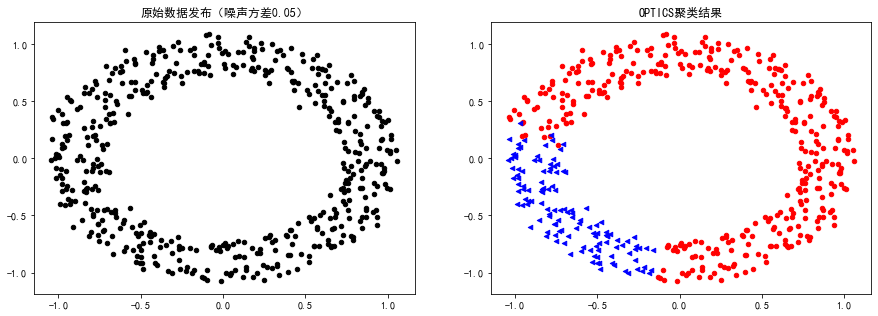
    X,labels = make_circles(n_samples = 500,noise = noise)
    plt.figure(figsize=(15,5))
    plt.subplot(121)
    plt.scatter(X[:,0],X[:,1],color = "black",s=20)
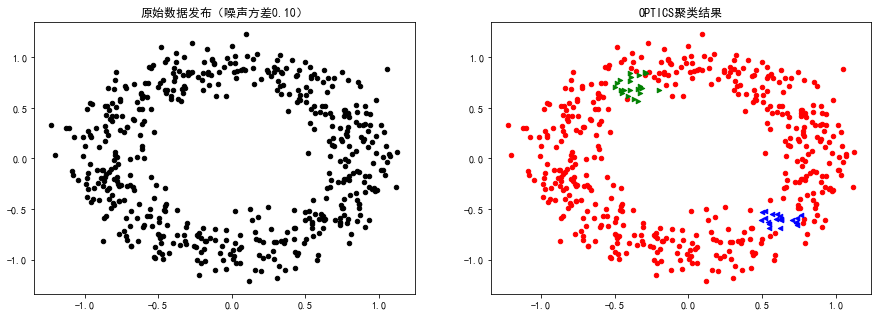
    plt.title("原始数据发布（噪声方差%.2f）"%noise)
    
    opt = cluster.OPTICS(min_samples = 20,max_eps = 0.5,cluster_method = 'xi',xi = 0.05)
    opt.fit(X)
    print('OPTICS类别标签(噪声%.2f):'%noise,np.unique(opt.labels_))
    plt.subplot(122)
    colors = ["b","g","c","m","y","k","r"]
    markers = ["<",">","s","+","*","^","o"]
    labels = ['簇1','簇2','簇3','簇4','簇5','簇6','噪声']
    for i,j in enumerate(opt.labels_):
        plt.scatter(X[i][0],X[i][1],color = colors[j],marker = markers[j],s = 20)
    plt.title("OPTICS聚类结果")
    plt.show()

运行结果：

OPTICS类别标签(噪声0.05): [-1  0]

OPTICS类别标签(噪声0.10): [-1  0  1]

OPTICS类别标签(噪声0.15): [-1  0  1  2  3  4]

案例2：

分别生成半月形、园环形数据、4类单标签数据以及正态分布的随机数据集;
分别使用k均值、BIRCH和DBSCAN算 法对4种不同形状的数据聚类;

#分别生成半月形、园环形数据、4类单标签数据以及正态分布的随机数据集;
#分别使用k均值、BIRCH和DBSCAN算 法对4种不同形状的数据聚类;
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn import cluster
from sklearn.datasets import make_blobs
from sklearn.datasets import make_moons
from sklearn.datasets import make_circles
#生成4种不同分布的数据
X1,labels = make_moons(n_samples = 500,noise = 0.1)#半月形分布数据
X2,labels = make_circles(n_samples = 500,factor = 0.2,noise = 0.05)#圆环形分布
X3,labels = make_blobs(n_samples = 500,centers=[[3,1],[-1,4],[0,-3],[-4,3]],n_features = 2,cluster_std = 1)
X4 = np.random.randn(300,2)#正态分布数据
#预定义12种颜色和形状，实际运行时可能出现聚类结果超过12种而报错的情况。
colors = ["b","g","r","c","m","y","k","lightgree","grey","pink","orange","purple"]
markers = ["o","s","D","+","*","^","<",">","1","2","3","4"]
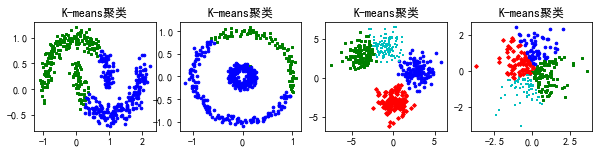
#使用k均值聚类对上述4种形状数据进行聚类分析
plt.figure(figsize = (10,2))
km = cluster.KMeans(n_clusters = 2,init = "k-means++",max_iter = 10,n_init = 1)
for index,data in enumerate([X1,X2,X3,X4]):
    if index>1:
        km.n_clusters = 4
    km.fit(data)
    plt.subplot(1,4,index+1)
    for i,j in enumerate(km.labels_):
        plt.scatter(data[i][0],data[i][1],color = colors[j],marker = markers[j],s = 7)
        plt.title('K-means聚类')
plt.show()
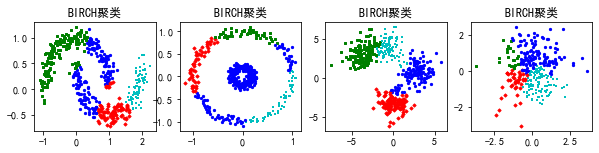
#使用BIRCH聚类对上述4种形状数据进行聚类分析
plt.figure(figsize = (10,2))    
bir = cluster.Birch(threshold = 0.5,n_clusters = 4,branching_factor = 60)
for index,data in enumerate([X1,X2,X3,X4]):
    if index>1:
        bir.n_clusters = 4
    bir.fit(data)
    plt.subplot(1,4,index+1)
    for i,j in enumerate(bir.labels_):
        plt.scatter(data[i][0],data[i][1],color = colors[j],marker = markers[j],s = 5)
        plt.title('BIRCH聚类')
plt.show()
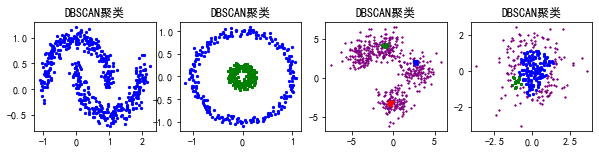
#使用DBSCAN聚类对上述4种形状数据进行聚类分析
plt.figure(figsize = (10,2))    
db = cluster.DBSCAN(eps = 0.3,min_samples = 10)
for index,data in enumerate([X1,X2,X3,X4]):
    db.fit(data)
    plt.subplot(1,4,index+1)
    for i,j in enumerate(db.labels_):
        plt.scatter(data[i][0],data[i][1],color = colors[j],marker = markers[j],s = 5)
        plt.title('DBSCAN聚类')
plt.show()

运行结果：

总结

以上就是今天的内容~

最后欢迎大家点赞👍，收藏⭐，转发🚀，
如有问题、建议，请您在评论区留言💬哦。