1.数据降维
通过自动数据收集和特征生成技术,可以快速获取大量特征,但不是所有特征都是有用的。数据降维就是在保留重要信息的同时消除那些“无信息量的信息”。
“无信息量”有多种定义方法,PCA 关注的是线性相关性,假设我们将数据矩阵的列空间描述为所有特征向量的生成空间。如果列空间的秩小于特征总数,那么多数特征就是几个关键特征的线性组合。线性相关的特征是对空间和计算能力的浪费,因为它们包含的信息可以从更少的几个特征中推导出来。为了避免这种情况,PCA 试图将数据挤压到一个维度大大小于原空间的线性子空间,从而消除这些“臃肿”。
PCA 的核心思想是,使用一些新特征代替冗余特征,这些新特征能恰当地总结初始特征空
间中包含的信息。当只有两个特征时,很容易找出新特征,但当初始特征空间中有成百上
千个维度时,就非常困难了。我们需要一种方法,先用数学语言描述要找出的新特征,然
后使用最优化技术来找出它们。
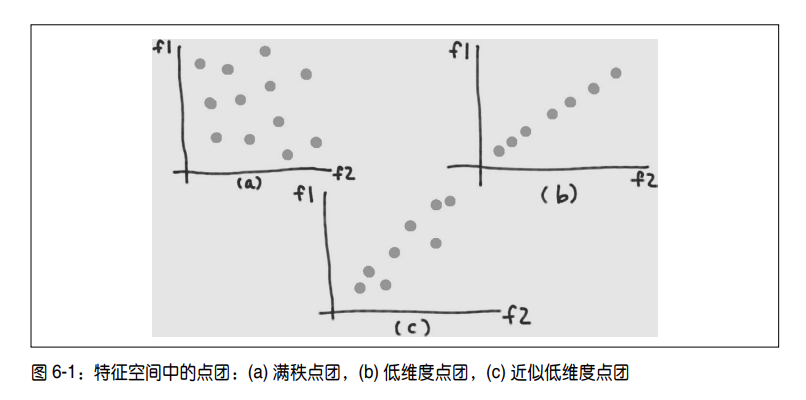
对“恰当地总结信息”的一种数学定义是,新的数据点团应该尽量多地保持原数据集中的
信息。我们将数据点团挤压成了一个扁平的饼,但我们希望这个饼在正确的方向上尽可能
地大。这意味着我们需要一种测量信息量的方式。信息量肯定与距离有关,但数据集合中的距离表示总是有点模糊。有人使用集合中任意两点之间距离的最大值,但事实证明这种函数很难进行数学优化。另一种方式是使用两点之间距离的平均值,或另一种等价形式——每个数据点与均值之间的平均距离,也就是方差;事实证明这种方式更容易进行优化。(生活本已艰难,幸好统计学家已经找到了捷径。)采用数学方式,这个问题就变成了使新特征空间中数据点的方差最大化。
2.PAC思想
PCA 关注的是线性相关性。将数据矩阵的列空间描述为所有特征向量的生成空间,如果列空间的秩小于特征总数,那么多数特征就是几个关键特征的线性组合。线性相关的特征是对空间和计算能力的浪费,因为它们包含的信息可以从更少的几个特征中推导出来。为了避免这种情况,PCA 试图将数据挤压到一个维度大大小于原空间的线性子空间,从而消除这些“臃肿”。
- PCA 的核心思想是,使用一些新特征代替冗余特征,这些新特征能恰当地总结初始特征空间中包含的信息。
在使用 PCA 进行数据降维时,必须确定要使用的主成分的数目(k)。和所有超参数一样,这个数目可以根据最终模型的质量来进行优化,但也有一些不需要昂贵计算成本的启发式方法。
- 选择 k 的一种可行方法是要求主成分能解释一定比例的总方差。
3.PCA降维实现
from sklearn import datasets
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib notebook
digits_data = datasets.load_digits()
n = len(digits_data.images)
print(n)
# 每个图像都表示为一个8×8的数组。将这个数组作为PCA的输入。
image_data = digits_data.images.reshape((n, -1))
print(image_data.shape)
# 真实值标签
labels = digits_data.target
labels
# 为这个数据集拟合一个PCA转换器
# 自动选择主成分的数目,使主成分能解释至少80%原来的方差\
pca_transformer = PCA(n_components=0.8)
pca_images = pca_transformer.fit_transform(image_data)
pca_transformer.explained_variance_ratio_
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(100):
ax.scatter(pca_images[i,0], pca_images[i,1], pca_images[i,2], marker=r'${}$'.format(labels[i]), s=64)
ax.set_xlabel('Principal component 1')
ax.set_ylabel('Principal component 2')
ax.set_zlabel('Principal component 3')
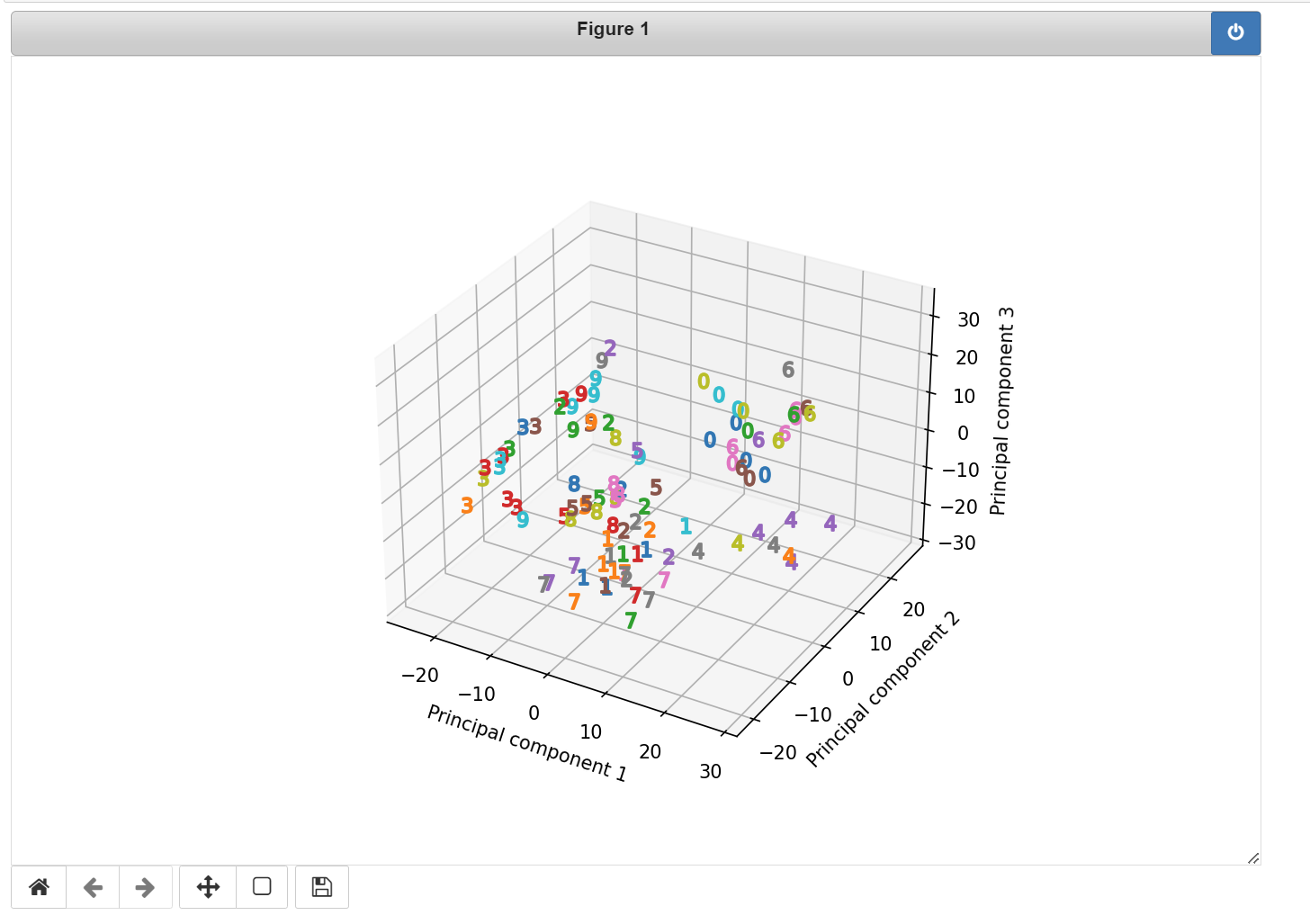
# 因为数字之间还有相当数量的重叠,所以在投影空间中使用线性分类器将数字区分开来还是很困难的。只使用前 3 个主成分作为特征是不够的。
# 所以这里仅仅是演示PCA的降维而已。
4.白化与ZCA
由于目标函数的正交限制,PCA 转换有一个非常好的副作用:转换后的特征都是不相关的。换句话说,每对特征向量之间的内积都是 0。
白化:一组特征,彼此之间的相关度为 0,与自身的相关度为 1。数学上,将PCA 转换乘以奇异值的倒数,就可以实现白化;
ZCA:是一种与 PCA 联系非常紧密的白化转换,但它不会减少特征的数量。ZCA 白化使用未削减的整个主成分集合,还要再乘上一个 V 的T次方 。白化与数据降维是彼此独立的,可以分别进行。
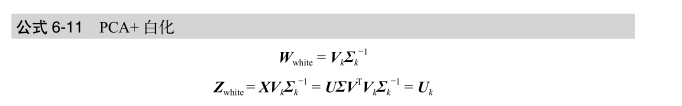
简单的 PCA 投影可以在新特征空间中以主成分为基生成坐标。这些坐标只表示投影向量的长度,不表示方向。乘以主成分之后,才能得到长度和方向。另一个合理解释是,这次相乘可以将坐标旋转回初始特征空间。(V 是一个正交矩阵,正交矩阵可以对输入进行没有拉伸和压缩的旋转。)所以,ZCA 生成的白化数据与初始数据是最接近的(用欧氏距离衡量)。
5.PCA的局限性与注意事项
在使用 PCA 进行数据降维时,必须确定要使用的主成分的数目(k)。和所有超参数一样,这
个数目可以根据最终模型的质量来进行优化,但也有一些不需要昂贵计算成本的启发式方法。
5.1谱分析确定降维个数K
选择 k 的一种可行方法是要求主成分能解释一定比例的总方差。(scikit-learn 的 PCA 包中有
这个选项。)在 k 个主成分上的投影的方差为:
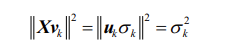
这个方差就是 X 第 k 大奇异值的平方。奇异值的排序列表称为矩阵的谱(spectrum)。因
此,要确定使用多少主成分,可以对数据矩阵做一个简单的谱分析,并选定能解释足够方
差的阈值。