数据结构与算法之美 | 递归(Recursion)

news2024/11/29 20:59:44

什么叫做递归？

递归：去的过程叫“递”，回来的过程叫“归”

递归的三个条件

条件一：一个问题的解可以分解为几个子问题的解
条件二：这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
条件三：存在递归终止条件

写递归的正确姿势

关键点：写出递推公式，找到终止条件

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码
只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤

假如有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？

假设 $f (n)$ 表示走 $n$ 个台阶的走法总数，那么有以下递推式：

$f (n) = f (n - 1) + f (n - 2)$

$f (n - 1)$ 表示先走一步，剩下的 $n - 1$ 个台阶就变成了一个子问题，即 $f (n - 1)$ ；
$f (n - 2)$ 表示先走两步，剩下的 $n - 2$ 个台阶也变成了一个子问题，即 $f (n - 2)$ 。最后的结果就是这两个子问题的总和。
边界条件是 $f (1) = 1$ ， $f (2) = 2$ 。因为只有一个台阶时只有一种走法，两个台阶时有两种走法，分别是一步一步走和直接跨两步。

用 Python 实现这个递推过程，可以写成如下代码：

def climbStairs(n):
    """
    计算爬楼梯的方案数
    :param n: 需要爬的楼梯数   
    :return: 爬楼梯的方案数
    """
    # 如果只有一级楼梯，只有一种爬法
    if n == 1:
        return 1
    # 如果有两级楼梯，有两种爬法
    if n == 2:
        return 2
    # 否则，根据递推公式计算爬楼梯的方案数
    return climbStairs(n-1) + climbStairs(n-2)

递归的副作用

堆栈溢出

问题原因：函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险

解决方法：在代码中限制递归调用的最大深度

使用Python代码实现：

import sys
# 进行递归深度限制
sys.setrecursionlimit(50)

def climbStairs(n):
    """
    计算爬楼梯的方案数，避免堆栈溢出。
    :param n: 需要爬的楼梯数   
    :return: 爬楼梯的方案数
    """
    # 如果只有一级楼梯，只有一种爬法
    if n == 1:
        return 1
    # 如果有两级楼梯，有两种爬法
    if n == 2:
        return 2
    # 否则，根据递推公式计算爬楼梯的方案数
    return climbStairs(n-1) + climbStairs(n-2)

但这种做法并不能完全解决问题，因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，事先无法计算。如果实时计算，代码过于复杂，就会影响代码的可读性。所以，如果最大深度比较小，比如 10、50，就可以用这种方法，否则这种方法并不是很实用。

重复计算

问题原因：在前述代码中，想要计算f(5)，需要先计算 f(4) 和 f(3)，而计算 f(4) 还需要计算 f(3)，因此，f(3) 就被计算了很多次，这就是重复计算问题。

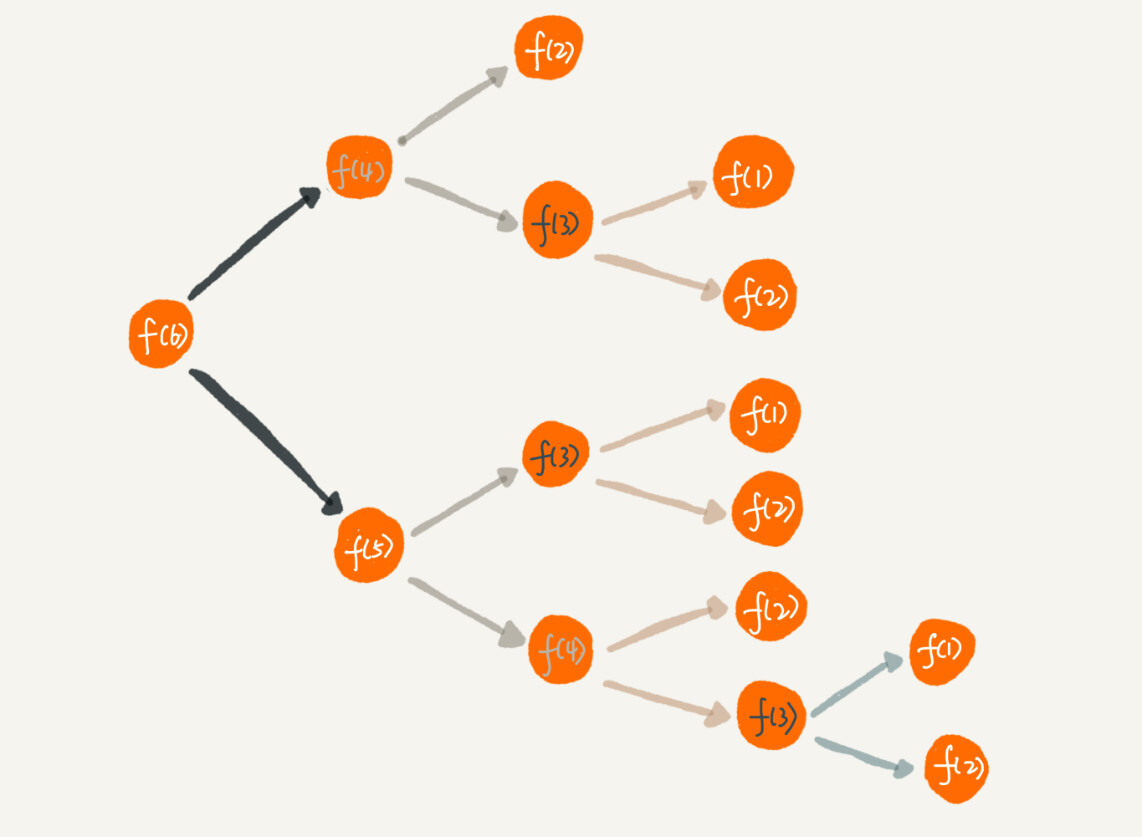
解决方法：可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算，这样就能避免刚讲的问题了。

使用Python代码实现：

def climb_stairs(n, memo):
    """
    计算爬楼梯的方案数，避免重复计算。
    :param n: 需要爬的楼梯数
    :param memo: 用于保存已经计算过的结果的散列表
    :return: 爬楼梯的方案数
    """
    if n in memo:
        # 如果已经计算过，直接返回结果
        return memo[n]
    if n == 1:
        # 如果只有一级楼梯，只有一种爬法
        memo[n] = 1
    elif n == 2:
        # 如果有两级楼梯，有两种爬法
        memo[n] = 2
    else:
        # 否则，根据递推公式计算爬楼梯的方案数
        memo[n] = climb_stairs(n - 1, memo) + climb_stairs(n - 2, memo)
    # 返回计算结果
    return memo[n]


n = 10
memo = {}
print(climb_stairs(n, memo))