---

买卖股票的最佳时机 III

力扣连接：123. 买卖股票的最佳时机 III（中等）

1.动态规划方法

1. 确定dp数组以及下标的含义
   一天一共就有五个状态，
   0：没有操作 （其实我们也可以不设置这个状态）
   1：第一次持有股票
   2：第一次不持有股票
   3：第二次持有股票
   4：第二次不持有股票
   dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

2. 确定递推公式
   达到dp[i][1]状态，有两个具体操作：
   操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
   操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

图解步骤

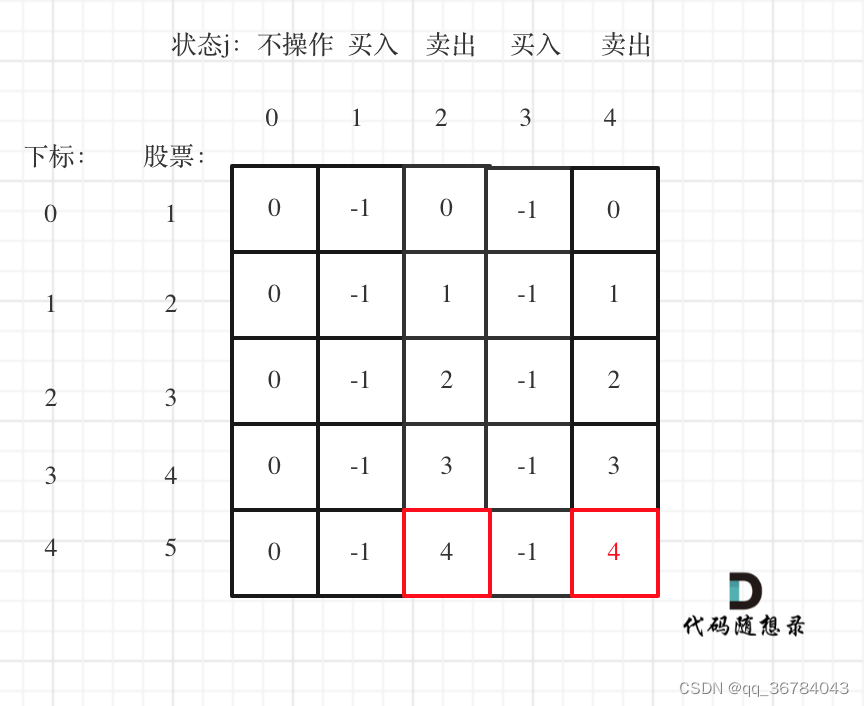
关键点：

• 初始化dp[0][2] 和 dp[0][4]的值为0

递归代码

class Solution {
    public int maxProfit(int[] prices) {
        int size = prices.length;
        int[][] dp = new int[size][5];

        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        dp[0][2] = 0; //当天买当天卖，手头上钱为0
        dp[0][3] = -prices[0];
        dp[0][4] = 0; //当天买当天卖，手头上钱为0

        for(int i=1;i<size;i++){
            dp[i][0] = 0;
            dp[i][1] = Math.max(dp[i-1][1], dp[i][0]-prices[i]);
            dp[i][2] = Math.max(dp[i-1][2], dp[i][1]+prices[i]);
            dp[i][3] = Math.max(dp[i-1][3], dp[i][2]-prices[i]);
            dp[i][4] = Math.max(dp[i-1][4], dp[i][3]+prices[i]);
        }

        return dp[size-1][4];

    }
}

---

---

买卖股票的最佳时机 IV

力扣连接：188. 买卖股票的最佳时机 IV（中等）

1.动态规划方法

和买卖III类似，将2次拓宽成k次（加for循环）即可

图解步骤

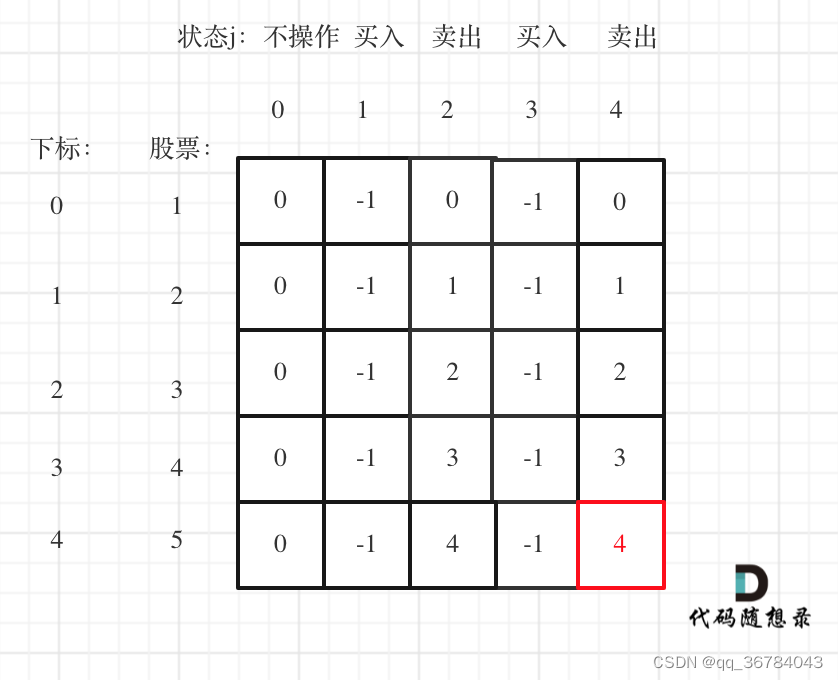
关键点：

• dp[0][j]当j为奇数的时候都初始化为 -prices[0]

代码

class Solution {
    public int maxProfit(int k, int[] prices) {
        int size = prices.length;
        int[][] dp = new int[size][2*k+1];

        dp[0][0] = 0;
        for(int j=1; j<2*k; j+=2){
            dp[0][j] = -prices[0];
        }

        for(int i=1;i<size;i++){
            for(int j=1;j<2*k;j+=2){
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]-prices[i]);
                dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i][j]+prices[i]);
            }
        }

        return dp[size-1][2*k];
    }
}

---

---