1.基本路径测试
2.画出程序控制流图
3.计算流图的环形复杂度
4.确定线性独立路径的基本集合
5.设计测试用例

基本路径测试

除了逻辑覆盖，还有一种常用的白盒测试的测试方法：基本路径测试。基本路径测试是 Tom McCabe提出的一种白盒测试技术。使用这种技术设计测试用例时，首先需要计算程序的环形复杂度，并用该复杂度为指南定义执行路径的基本集合，从该基本集合导出的测试用例可以保证程序中的每条语句至少执行一次，而且每个条件在执行时都将分别取真、假两种值。

画出程序控制流图

流图其实就是程序的流程图的简化版。其中只用圆圈来表示程序中的代码语句。
我们不妨通过一个例子带大家画出程序的流图。程序如下图所示：

这段代码的功能是计算不超过100个在规定值域内的有效数字的平均值。
代码中有一个while结构，两个if结构，在流图中能体现出这三个结构的话，流图就算是画出来了，如下所示：
 

计算环形复杂度

画出程序控制流的流图后，下一步便是计算流图的环形复杂度。环形复杂度定量度量程序的逻辑复杂性。使用基本路径测试法设计测试用例时，程序的环形复杂度决定了程序中独立路径的数量，而且这个数是确保程序中所有语句至少被执行一次所需的测试数量的上界。
有以下两种方法计算环形复杂度：

给定流图G的环形复杂度V(G)，定义为V(G)=E-N+2，E是流图中边的数量，N是流图中结点的数量；

给定流图G的圈复杂度V(G)，定义为V(G)=P+1，P是流图G中判定结点的数量。

上面的流图的环形复杂度，可以分别使用这两种方法进行计算：

方法一：环形复杂度= 17 条边 - 13 个节点 + 2 ，即环形复杂度为 6；
方法二：环形复杂度= 6 个判定节点 + 1，即环形复杂度为 6。

确定独立路径

计算好流图的环形复杂度，便可以知晓程序独立路径的条数。所谓独立路径就是从流图开始的地方到结束的地方的通路。独立路径的数量等于流图的环形复杂度。上面例子的环形复杂度为6，所以独立路径总共有6条。
下面列出这6条独立路径：

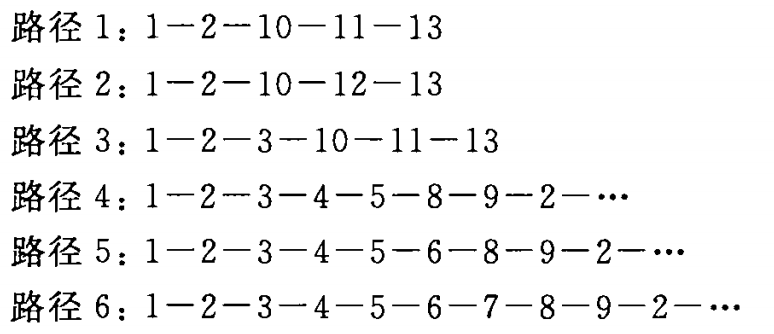
路径4、5、6后的省略号表示可以后接通过控制结构其余部分的任意路径。

设计测试用例

确定了独立路径后，就需要设计多组测试用例，覆盖所有的独立路径。每组测试用例覆盖一条独立路径。因此测试用例可以是：
路径1的测试用例：
value[k] = 有效输入值
value[i] = -999
预期结果：基于k的正确平均值和总数
路径2的测试用例：
value[1] = -999
预期结果：avarage = -999
路径3的测试用例：
试图处理101个或更多值
预期结果：前100个数的平均值，总数为100
路径4的测试用例：
value[i] = 有效输入值,i<100
value[k] < minimum,k<i
预期结果：基于k的正确平均值和总数
路径5的测试用例：
value[i] = 有效输入值,i<100
value[k] > maximum,k<i
预期结果：基于k的正确平均值和总数
路径6的测试用例：
value[i] = 有效输入值，i<100
预期结果：正确的平均值和总数

至此，我们便完整的走完了一遍基本路径测试法的全部流程。

作答要求

使用基本路径测试法，设计满足基本路径测试的多个测试用例，用于对test函数进行白盒测试。函数代码如下：

测试结果

1. public static void test(int numA,int numB){
2. int x = 0;
3. int y = 0;
4. while(numA-- > 0)
5. {
6. if(numB == 0)
7. x = y + 1;
8. else
9. if(numB == 1)
10. x = y + 2;
11. else
12. x = y + 3;
13. }
14. }

16. 1、

    该程序的流图的环形复杂度和独立路径条数分别是多少？

    A、

    3，3

    B、

    4，4

    C、

    5，5

    D、

    6，6

17. 2、

    以下哪种测试用例的设计可以覆盖所有的独立路径？

    A、

    TestCase1: numA = 0, numB = 1
    TestCase2: numA = 1, numB = 0
    TestCase3: numA = 1, numB = 1
    TestCase4: numA = 1, numB = 2

    B、

    TestCase1: numA = 0, numB = 0
    TestCase2: numA = 1, numB = 0
    TestCase3: numA = 1, numB = 1

    C、

    TestCase1: numA = 1, numB = 0
    TestCase2: numA = 1, numB = 1
    TestCase3: numA = 1, numB = 2

    D、

    TestCase1: numA = 0, numB = 0
    TestCase2: numA = 0, numB = 1
    TestCase3: numA = 0, numB = 2
    TestCase4: numA = 1, numB = 0