2022年国赛高教杯数学建模
A题 波浪能最大输出功率设计
原题再现
随着经济和社会的发展,人类面临能源需求和环境污染的双重挑战,发展可再生能源产业已成为世界各国的共识。波浪能作为一种重要的海洋可再生能源,分布广泛,储量丰富,具有可观的应用前景。波浪能装置的能量转换效率是波浪能规模化利用的关键问题之一。
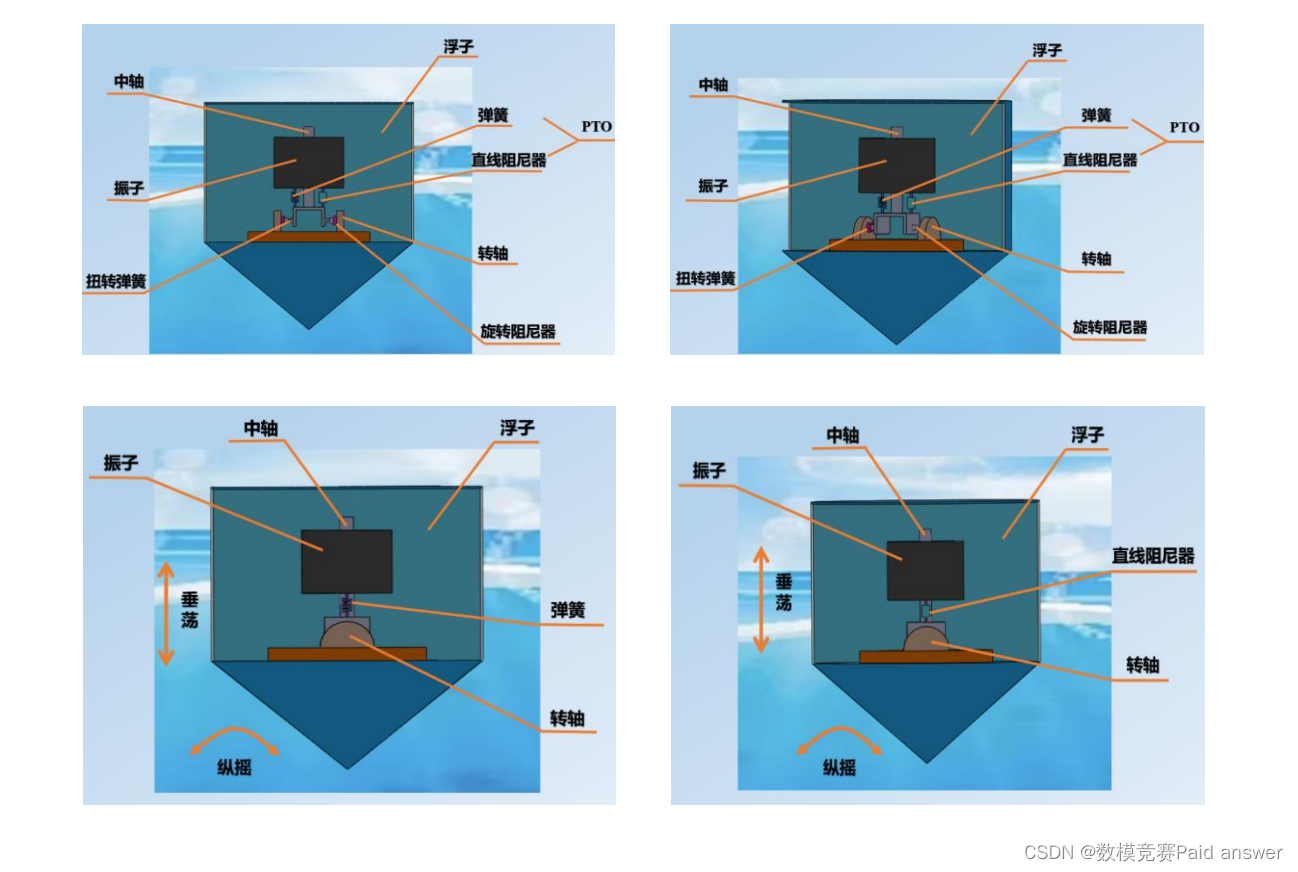
图 1 为一种波浪能装置示意图,由浮子、振子、中轴以及能量输出系统(PTO,包括弹簧和阻尼器)构成,其中振子、中轴及 PTO 被密封在浮子内部;浮子由质量均匀分布的圆柱壳体和圆锥壳体组成;两壳体连接部分有一个隔层,作为安装中轴的支撑面;振子是穿在中轴上的圆柱体,通过 PTO 系统与中轴底座连接。在波浪的作用下,浮子运动并带动振子运动(参见附件 1 和附件 2),通过两者的相对运动驱动阻尼器做功,并将所做的功作为能量输出。考虑海水是无粘及无旋的,浮子在线性周期微幅波作用下会受到波浪激励力(矩)、附加惯性力(矩)、兴波阻尼力(矩)和静水恢复力(矩)。在分析下面问题时,忽略中轴、底座、隔层及 PTO 的质量和各种摩擦。

请建立数学模型解决以下问题:
问题 1 如图 1 所示,中轴底座固定于隔层的中心位置,弹簧和直线阻尼器一端固定在振子上,一端固定在中轴底座上,振子沿中轴做往复运动。直线阻尼器的阻尼力与浮子和振子的相对速度成正比,比例系数为直线阻尼器的阻尼系数。考虑浮子在波浪中只做垂荡运动(参见附件 1),建立浮子与振子的运动模型。初始时刻浮子和振子平衡于静水中,利用附件 3 和附件 4 提供的参数值(其中波浪频率取 1.4005 s−1,这里及以下出现的频率均指圆频率,角度均采用弧度制),分别对以下两种情况计算浮子和振子在波浪激励力 𝑓 cos 𝜔𝑡(𝑓 为波浪激励力振幅,𝜔 为波浪频率)作用下前 40 个波浪周期内时间间隔为 0.2 s 的垂荡位移和速度:(1) 直线阻尼器的阻尼系数为 10000 N·s/m;(2) 直线阻尼器的阻尼系数与浮子和振子的相对速度的绝对值的幂成正比,其中比例系数取 10000,幂指数取 0.5。将结果存放在 result1-1.xlsx 和result1-2.xlsx 中。在论文中给出 10 s、20 s、40 s、60 s、100 s 时,浮子与振子的垂荡位移和速度。
问题 2 仍考虑浮子在波浪中只做垂荡运动,分别对以下两种情况建立确定直线阻尼器的最优阻尼系数的数学模型,使得 PTO 系统的平均输出功率最大:(1) 阻尼系数为常量,阻尼系数在区间 [0,100000] 内取值;(2) 阻尼系数与浮子和振子的相对速度的绝对值的幂成正比,比例系数在区间 [0,100000] 内取值,幂指数在区间 [0,1] 内取值。利用附件 3 和附件 4 提供的参数值(波浪频率取 2.2143 s−1)分别计算两种情况的最大输出功率及相应的最优阻尼系数。
问题 3 如图 2 所示,中轴底座固定于隔层的中心位置,中轴架通过转轴铰接于中轴底座中心,中轴绕转轴转动,PTO 系统连接振子和转轴架,并处于中轴与转轴所在的平面。除了直线阻尼器,在转轴上还安装了旋转阻尼器和扭转弹簧,直线阻尼器和旋转阻尼器共同做功输出能量。在波浪的作用下,浮子进行摇荡运动,并通过转轴及扭转弹簧和旋转阻尼器带动中轴转动。振子随中轴转动,同时沿中轴进行滑动。扭转弹簧的扭矩与浮子和振子的相对角位移成正比,比例系数为扭转弹簧的刚度。旋转阻尼器的扭矩与浮子和振子的相对角速度成正比,比例系数为旋转阻尼器的旋转阻尼系数。考虑浮子只做垂荡和纵摇运动(参见附件 2),建立浮子与振子的运动模型。初始时刻浮子和振子平衡于静水中,利用附件 3 和附件 4 提供的参数值(波浪频率取 1.7152 s−1),假定直线阻尼器和旋转阻尼器的阻尼系数均为常量,分别为 10000 N·s/m和 1000 N·m·s,计算浮子与振子在波浪激励力和波浪激励力矩 𝑓 cos 𝜔𝑡,𝐿 cos 𝜔𝑡(𝑓 为波浪激励力振幅,𝐿 为波浪激励力矩振幅,𝜔 为波浪频率)作用下前 40 个波浪周期内时间间隔为 0.2 s 的垂荡位移与速度和纵摇角位移与角速度。将结果存放在 result3.xlsx 中。在论文中给出 10 s、20 s、40 s、60 s、100 s 时,浮子与振子的垂荡位移与速度和纵摇角位移与角速度。
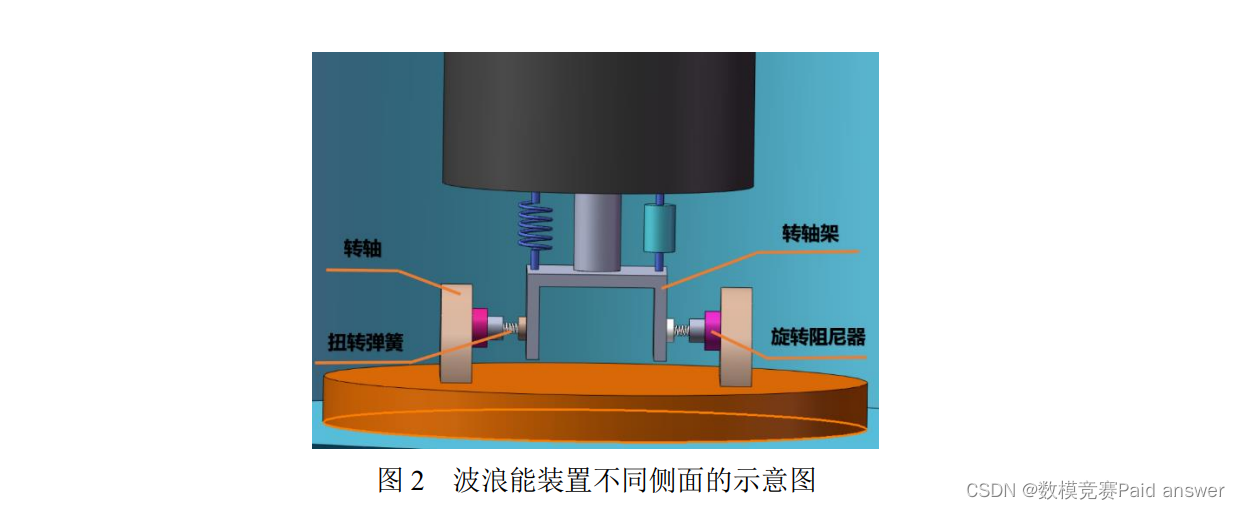
问题 4 考虑浮子在波浪中只做垂荡和纵摇的情形,针对直线阻尼器和旋转阻尼器的阻尼系数均为常量的情况,建立确定直线阻尼器和旋转阻尼器最优阻尼系数的数学模型,直线阻尼器和旋转阻尼器的阻尼系数均在区间 [0,100000] 内取值。利用附件 3 和附件 4 提供的参数值(波浪频率取 1.9806 s−1)计算最大输出功率及相应的最优阻尼系数。
附件 1 垂荡的动画
附件 2 垂荡和纵摇的动画
附件 3 不同入射波浪频率下的附加质量、附加转动惯量、兴波阻尼系数、波浪激励力(矩)振幅
附件 4 浮子和振子的物理参数和几何参数值
整体求解过程概述(摘要)
本文在求波浪能最大输出功率设计中,通过受力分析,建立了浮子和振子的垂荡和纵摇运动模型,并通过四阶龙格库塔算法将建立的连练微分方程离散化处理,递推求出了相应时间内浮子和振子的垂荡纵摇运动情况。同时对功率的积分函数值以微小步长为底的梯形面积替代,通过遗传算法搜索参数,求出了最大输出功率和相应的最优阻尼系数,并对模型进行了检验和误差分析。
针对问题一:首先,基于对坐标系灵活选取,通过牛顿第二定律,建立浮子和振子相互作用的垂荡运动模型。其次,根据模型及初始运动状态确定了垂荡运动的二元二阶力学微分方程。最后,利用改进的龙格库塔算法对处理后的方程进行选代求解,得到了浮子和振子在前40个周期内时间间隔为0.2s的垂荡位移和速度。结果详细见表2。
针对问题二:在浮子和振子相互作用的垂荡运动模型基础上,推导出了直线阻尼平均输出功率积分函数,建立了以垂荡运动装置的平均输出功率最大为目标的单目标优化模型。同时为求解该积分值,本文利用微小值作为底的梯形面积近似代替该函数值,且选取100s后的稳定状态作为区间求出平均输出功率,所需数值可由垂荡运动模型确定。最后,利用遗传算法搜索参数,确定在(1)条件下,最大平均输出功率为229.6819w,最优直线阻尼系数为37639;在(2)条件下,最大平均输出功率为230.0163w,最优直线阻尼系数为81478,幂指数为0.3377。
针对问题三:首先,基于刚体转动的平行移轴定理和垂直轴定理、组合体重心计算公式,得到浮子和振子的纵摇运动的转动惯量函数。其次,基于牛顿第二定律,建立浮子和振子的纵摇运动模型。再进一步,确定了垂荡和纵据之间的联系,得到该模型方程为四元二阶微分方程。最后,利用龙格塔库草法选代求解该微分方程前40个波浪周期内时间间隔为0.2s的垂荡位移与速度、纵摇角位移与角速度。结果见表3。
针对问题四:在浮子和振子的纵摇模型的基础上,同样推导出了旋转阻尼平均输出功率积分函数,在同时考虑垂荡和纵摇基础上,建立了以同时考虑摇荡和纵摇运动的平均输出功率最大为目标的单目标优化模型。为求解该积分函数,对连续功率函数进行与问题二相同的离散化处理,且选取100s后的稳定状态作为区间求出平均输出功率,所需数值可由垂荡、纵摇运动模型得出。最后,采用遗传搜索算法求解,确定最大平均输出功率为316.5807w,最优直线阻尼系数为58944,最优旋转阻尼系数为98227。
模型假设:
1.由于作用于浮子的波浪为线性周期微幅波,忽略波面的升高
2.流场内海水是理想流体,无粘、无旋、不可压缩。
3.忽略纵摇运动对垂荡运动的影响
4.忽略中轴、底座、隔层及 PTO 的质量和各种摩擦。
问题分析:
问题一分析:
问题一需要根据波浪激励力建立浮子与振子运动模型。本题难点在于准确反映浮子和振子振动的物理过程。对此,灵活选取坐标系,基于牛顿第二定律,建立浮子和振子垂荡运动二阶二元微分方程。继而对微分方程采用改进的四阶龙格塔库算法求解,实现了高精度的要求。
问题二分析:
在问题一的基础上,需要利用附件三和附件四的参数值,求出指定情况下能使系统平均输出功率最大的最优阻尼系数。本题选定通过合理的时间区间,推导平均功率函数,继而建立直线阻尼器阻尼系数的优化模型,利用龙格塔库法粗略寻优后采用遗传算法,分别求出阻尼系数为常量、阻尼系数随相对速度变化时两种情况下的最大平均输出功率以及对应的最优阻尼系数。
问题三分析:
本题需进一步考虑纵摇运动。对此基于牛顿第二定律,建立纵摇运动模型,并利用组合体的重心计算公式、刚体转动的垂直轴定理和平行移轴定理,实现振荡浮子式波浪能发电装置的转动惯量的计算。最后用改进的四阶龙格塔库算法实现问题三的求解,
问题四分析
在问题三的基础上,针对直线阻尼器和旋转阻尼器的系数均为常量的情况,需要确定指定取值范围内,使平均输出功率最大的最优阻尼系数。对此,建立阻尼系数的优化模型,选取系统稳定响应后的一段时间计算垂荡运动、纵摇运动的平均输出功率,利用龙格塔库法粗略寻优后,采用遗传算法快速求解得到最大输出功率和相应的最优阻尼系数。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
function [T,X,dX] = ODE_ImprovedEuler( Hfun,t,h,x0 )
% [T,X,dX] = ODE_ImprovedEuler( Hfun,t,h,x0 ) 改进欧拉法求解常微分方程
% Hfun为描述一阶微分方程导数的函数句柄,格式为 dX = Hfun( t,X )
% t为时间节点,可为标量,时间范围为 T = 0:h:t
% 长2向量 ,时间范围为 T = t(1):h:t(2)
% 向量 ,时间范围为 T = t
% h为时间步长,在t的前两种情况下,必须给出h具体值
% 直接给出时间节点t时,h可用[]或任意值占位
% x0为状态量初始值
% 算法:
% Xp = X(k-1) + h*dX(k-1)
% dXp = Hfun( T(k),Xp )
% X(k) = X(k-1) + (h/2)*[dX(k-1)+dXp]
% By ZFS@wust 2021
% 获取更多Matlab/Simulink原创资料和程序,清关注微信公众号:Matlab Fans
if nargin < 4
error('初始值必须给出');
end
% 确定时间节点
n = length(t);
if n == 1
T = 0:h:t;
elseif n == 2
T = t(1):h:t(2);
else
T = t;
end
T = T(:); % 时间变为列向量
% 计算
N = length(T);
x0 = x0(:); x0 = x0'; % 初值变为行向量
m = length(x0); % 状态量维数
X = zeros(N,m); % 初始化状态量
dX = zeros(N,m); % 状态导数
X(1,:) = x0;
for k = 2:N
dX(k-1,:) = Hfun( T(k-1),X(k-1,:) );
h = T(k) - T(k-1);
Xp = X(k-1,:) + h*dX(k-1,:);
dXp = Hfun( T(k),Xp );
X(k,:) = X(k-1,:) + (h/2)*(dX(k-1,:)+dXp');
end
dX(N,:) = Hfun( T(N),X(N,:) );
if nargout == 0
plot(T,X)
end
function [T,X,dX] = ODE_RK4( Hfun,t,h,x0 )
% [T,X] = ODE_RK4( Hfun,t,h,x0 ) 4阶龙格-库塔法求解常微分方程
% Hfun为描述状态导数的函数句柄,格式为 dX = Hfun( t,X )
% 必须保证返回dX的格式为行向量
% t为时间节点,可为标量,时间范围为 T = 0:h:t
% 长2向量 ,时间范围为 T = t(1):h:t(2)
% 向量 ,时间范围为 T = t
% h为时间步长,在t的前两种情况下,必须给出h具体值
% 直接给出时间节点t时,h可用[]或任意值占位
% x0为状态量初始值
% 算法:
% K1 = Hfun( t(k-1),X(k-1) ) = dX(k-1)
% K2 = Hfun( t(k-1)+h/2,X(k-1)+h*K1/2 )
% K3 = Hfun( t(k-1)+h/2,X(k-1)+h*K2/2 )
% K4 = Hfun( t(k-1)+h ,X(k-1)+h*K3 )
% X(k) = X(k-1) + (h/6) * (K1 + 2*K2 + 2*K3 +K4)
if nargin < 4
error('初始值必须给出');
end
if isstr(Hfun)
eval(['Hfun = @',Hfun,';']);
end
% 确定时间节点
n = length(t);
if n == 1
T = 0:h:t;
elseif n == 2
T = t(1):h:t(2);
else
T = t;
end
T = T(:); % 时间变为列向量
% 计算
N = length(T);
x0 = x0(:);
x0 = x0'; % 初值变为行向量
m = length(x0); % 状态量维数
X = zeros(N,m); % 初始化状态量
dX = zeros(N,m); % 状态导数
X(1,:) = x0;
for k = 2:N
h = T(k) - T(k-1);
K1 = Hfun( T(k-1) , X(k-1,:)' );
K2 = Hfun( T(k-1)+h/2 , X(k-1,:)'+h*K1/2 );
K3 = Hfun( T(k-1)+h/2 , X(k-1,:)'+h*K2/2 );
K4 = Hfun( T(k-1)+h , X(k-1,:)'+h*K3 );
X(k,:) = X(k-1,:)' + (h/6) * ( K1 + 2*K2 + 2*K3 + K4 );
dX(k-1,:) = (1/6) * ( K1 + 2*K2 + 2*K3 + K4 );
end
dX(N,:) = Hfun( T(N),X(N,:) );
if nargout == 0
plot(T,X)
end