位运算
- 有符号整数
- 无符号整数
- 位移运算
1计算机中数字的表示
-
计算机只有0,1两个数字,所以我们常用的10进制计算
-
所以我们需表示10进制
-
要使用二进制来表示10进制数
进制表示法
我们假设一个 8 位的数据类型
方案1
2:
0000 0010我们会发现这样无法表示负数
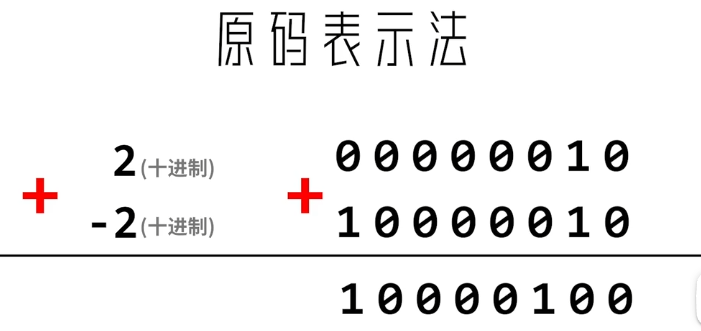
方案2:原码表示法
最高位表示正负(0正1负),剩余7位表示数值
2:
0000 0010-2:
1000 0010计算2+(-2)
我们发现结果为
1000 0100,翻译为10进制为 -4 ;同样出现了问题方案三:补码表示法
- 补码规则:正数的补码与原码一样;负数:对其绝对值按位取反,+1;
- 反码:符号位不变,其余位数取反(0—>1,1—>0)
- 补码:反码+1
-3
先计算-3绝对值的二进制 00000011
取反:11111100
加1:11111101(这就是计算级的-3表示)
2. 规则总结(有符号数)
- 二进制最高位是符号位:0正1负
- 正数的原码,反码,补码都一样
- 负数的反码:符号位不败,其余取反
- 负数的补码:反码+1
- 0的补码,反码都是0
- 计算机运算时使用补码来运算
3. 有符号运算案例
1+1
1的补码:
0000 0001
0000 0001+0000 0001=0000 0010即10进制的2
1-2
- 将两个数转换为补码
1的补码:
0000 0001-2 的原码:
1000 0010-2的反码:
1111 1101-2的补码:
1111 1110
1111 1110+0000 0001=1111 1111
- 将结果反推回去
先-1 的到反码
1111 1110在得到原码
1000 0001即 10进制表示的 -1(答案正确)
位运算
-
逻辑运算符
- &:与,
- ^:异或,无进位加法
- |:或:有1则为1
-
位移运算符
- <<:左移

- 在一些特殊情况下 可以当作*2 使用,但是需要注意二者并不等价,比如 我们左移30位 数字正负都会发生变化
- 规矩这个规则,任意一个10进制数都会变为0,所以当int 左移位数大于等于32位时,会先求余数,在进行左移即
- 左移32位相当于不移动
- 33位相当于移动1位
-
>>:右移
-
>>>:无符号右移
正数
10 :
0000 101010>>2
0000 0010—>210>>>2
0000 0010—>2我们可以发现对于正数而言其结果一样
负数
-10 原码 :
1000 1010 反码:
1111 0101 补码:
1111 0110-10 >>2
1111 1101(取前6位,高位补1) —》变换回原数:-3-10 >>2
0011 1101(取前6位,高位补0)—> 195负数二者运算结果不一样