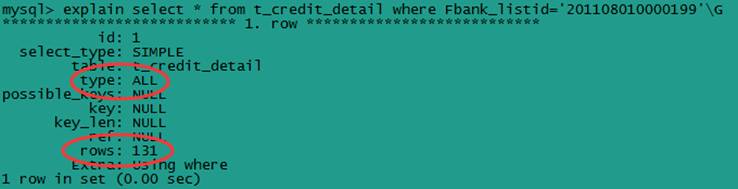
78 子集

与组合问题相比，需要保存路上经过的所有节点。

写法1

分为选择第 $i$ 个元素和不选择第 $i$ 个元素两种情况递归。

每push进一个元素，代表进入了一个新的节点，就保存当前的路径。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> set = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        // 空集
        res.add(new ArrayList<>());
        DFS(nums, 0);
        return res;
    }

    public void DFS(int[] nums, int i) {
        // 从DFS[i: n]遍历可得到的子集
        if (i == nums.length) {
            return;
        }

        // 选择第i个元素
        set.push(nums[i]);
        res.add(new ArrayList<>(set));
        DFS(nums, i + 1);

        // 不选择第i个元素
        set.pop();
        DFS(nums, i + 1);
    }
}

写法2

写成循环的形式。

含1的子集；不含1含2的子集，不含12含3的子集……

栗子， ${1,2,3,4,5,6,7,8,9,10\}$ 的子集：

选择1，加上 ${2,3,4,5,6,7,8,9,10\}$ 的所有子集；
选择2，加上 ${3,4,5,6,7,8,9,10\}$ 的所有子集；
选择3，加上 ${4,5,6,7,8,9,10\}$ 的所有子集；
$\dots$

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> set = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        // 空集
        res.add(new ArrayList<>());
        DFS(nums, 0);
        return res;
    }

    public void DFS(int[] nums, int start) {
        // 从DFS[i: n]遍历可得到的子集
        if (start == nums.length) {
            return;
        }

        for (int i = start;  i < nums.length; i++) {
            // 选择第i个元素
            set.push(nums[i]);
            res.add(new ArrayList<>(set));
            DFS(nums, i + 1);
            set.pop();
        }
    }
}

90 子集Ⅱ

与组合总和Ⅱ去重很像，基本是一样的思路。

先排序，然后同层中遍历的树枝值不可以相同。

去重的key：i > start && nums[i] == nums[i - 1]时continue，这样保证了同一层中不会有相同值的树枝。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> path = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        res.add(new ArrayList<>());
        DFS(nums, 0);
        return res;
    }

    public void DFS(int[] nums, int start) {
        // nums[start:]的所有子集
        if (start >= nums.length) {
            return;
        }

        for (int i = start; i < nums.length; i++) {
            // 如果与上一个元素相同，不要再递归访问啦
            if (i > start && nums[i - 1] == nums[i]) {
                continue;
            }

            path.push(nums[i]);
            res.add(new ArrayList<>(path));
            DFS(nums, i + 1);
            path.pop();
        }
    }
}

46 全排列

数字不重复。

使用辅助数组used，递归终止条件为stack.size() == nums.length。

遍历每个数字，判断是否被使用过，没有使用过的话就加入并继续向下递归。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    boolean[] used;
    Stack<Integer> stack = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();
    int[] nums;

    public List<List<Integer>> permute(int[] nums) {
        used = new boolean[nums.length];
        this.nums = nums;
        DFS();
        return res;
    }

    public void DFS() {
        if (stack.size() == nums.length) {
            res.add(new ArrayList<>(stack));
            return;
        }
        // 没有办法，只能遍历每个数字，判断是否被使用过，没有使用过的话就加入并继续向下递归
        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            stack.push(nums[i]);
            used[i] = true;
            DFS();
            stack.pop();
            used[i] = false;
        }
    }
}

47 全排列Ⅱ

去重思路和之前做过的很像，在同一层中不重复访问数字。同一层的相同树枝去重。

关键在于：

			// 如果和前一个数字相同，并且在这一层中，前一个数字已经被遍历过
            // !used[i - 1]代表与前一个数字不在同一个递归子树上
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }

因为前一个如果未被used过，说明前一个数字的树枝已经被访问过，且与当前数字不在同一树枝，不必再遍历。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

class Solution {
    boolean[] used;
    Stack<Integer> stack = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();
    int[] nums;


    public List<List<Integer>> permuteUnique(int[] nums) {
        this.nums = nums;
        this.used = new boolean[nums.length];
        Arrays.sort(this.nums);
        DFS();
        return res;
    }

    public void DFS() {
        if (stack.size() == nums.length) {
            res.add(new ArrayList<>(stack));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            // 如果这个数字已经被使用过，跳过
            if (used[i]) {
                continue;
            }
            // 如果和前一个数字相同，并且在这一层中，前一个数字已经被遍历过
            // !used[i - 1]代表与前一个数字不在同一个递归子树上
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            used[i] = true;
            stack.push(nums[i]);
            DFS();
            stack.pop();
            used[i] = false;
        }
    }
}