系列文章目录
- 数字信号处理中的 SIMD
- Neon intrinsics 简明教程
文章目录
- 系列文章目录
- 写在前面
- 前言
- FIR 滤波器
- 优化方案
- 何时应该使用时域的滤波器?
- 如何加快FIR滤波器的实现速度?
- 初步假设
- 有限长度信号
- 反转的滤波器系数
- 实际的卷积公式
- 卷积过程可视化
- 线性卷积最简单的实现
- 循环向量化
- Inner loop vectorization (VIL)
- VIL NEON 实现
- Outer Loop Vectorization (VOL)
- VOL NEON Implementation
- Outer and Inner Loop vectorization (VOIL)
- 为什么 VOIL 更优?
- 数据对齐
- VOIL NEON Implementation
- 总结
- 参考
写在前面
本文多数内容翻译自 Efficient FIR Filter Implementation with SIMD。原文在 SIMD 代码实现中使用到了 AVX,本文将使用 NEON 实现,关于 NEON 如何使用,请参考 Neon intrinsics 简明教程。
前言
如何让你的 FIR 滤波器在时域中更快的运行?
FIR 滤波器是数字信号处理中的基石。它在将混响应用于音频信号时尤其重要,例如在虚拟现实音频或数字音频工作站的VST插件中。它还被广泛用于移动电话(甚至是前智能手机!)和嵌入式设备的声音应用。
如何让 FIR 运行地更快呢?
FIR 滤波器
FIR 滤波器由它的有限长脉冲响应信号
h
[
n
]
h[n]
h[n] 定义,FIR 滤波器的输出
y
[
n
]
y[n]
y[n] 是输入信号
x
[
n
]
x[n]
x[n] 与脉冲响应的卷积。我们把它写成:
y
[
n
]
=
x
[
n
]
∗
h
[
n
]
=
∑
k
=
−
∞
∞
x
[
k
]
h
[
n
−
k
]
y[n]=x[n] * h[n]=\sum_{k=-\infty}^{\infty} x[k] h[n-k]
y[n]=x[n]∗h[n]=k=−∞∑∞x[k]h[n−k]
关于卷积的知识你可以参考我之前发的文章 【音频处理】Fast Convolution 快速卷积算法简介 或者 Convolution: The secret behind filtering
优化方案
如果你想让任何软件尽可能快地执行,有两种方法可以实现。
- 最佳的算法
- 高效的执行
同样的原则也适用于 DSP 代码。要想在代码中拥有一个快速的有限脉冲响应(FIR)滤波器,你可以这样做:
- 使用一种时间复杂度更低的算法,例如通过傅里叶变换到频域后进行快速卷积,或者
- 或者,利用硬件和软件资源的优势来有效地实现时域卷积。这通常意味着使用 SIMD 指令对你的代码进行矢量化。
何时应该使用时域的滤波器?
你或许会这么问自己:
既然我们有一个快速卷积算法,为什么我们还需要一个时域的实现呢?
快速卷积的算法复杂度是 O ( N log N ) O(N\log N) O(NlogN),其中 N 可能输入信号或滤波器的长度。而线性卷积的算法复杂度是 O ( N 2 ) O(N^2) O(N2)
首先,这意味着对于足够小的 N N N,线性卷积算法将比快速卷积算法更快。
其次,快速卷积在复数域上操作,而线性卷积总是使用实数。这实际上意味着,快速卷积需要处理的数据是线性卷积的两倍。
如果时域卷积可能比快速卷积更快这一事实让你感到困惑,请想想排序算法。一般来说,快排被认为是最快的排序算法。但是如果你看一下排序的实现,比如std::sort,你会发现它最初只使用quicksort。在将排序的容器划分为足够小的部分后,会使用插入排序对其中的元素进行排序。
在解释了这一点之后,我们可以研究如何在时域中有效地实现FIR滤波。
如何加快FIR滤波器的实现速度?
简而言之:通过 SIMD。
加快滤波器执行速度的最好方法是使用 SIMD 指令一次处理多个样本。为了实现这一点,我们需要重写线性卷积算法,使我们的代码在向量上运行。
这个过程被称为循环向量化。
循环向量化通常由编译器完成,但这种自动向量化的程度通常对实时 DSP 来说是不够的。相反,我们需要准确地指示编译器要做什么。
SIMD 指令在对对齐的数据进行操作时能达到最佳性能。因此,数据对齐是我们应该考虑的另一个因素。
总之,一个高效的FIR滤波器的实现要同时使用两种策略。
- 循环矢量化
- 数据对齐
现在我们将详细讨论这两种策略。
初步假设
线性卷积公式如下:
x
[
n
]
∗
h
[
n
]
=
∑
k
=
−
∞
∞
x
[
k
]
h
[
n
−
k
]
=
y
[
n
]
,
n
∈
Z
.
(1)
x[n] * h[n]=\sum_{k=-\infty}^{\infty} x[k] h[n-k]=y[n], \quad n \in \mathbb{Z} . \tag{1}
x[n]∗h[n]=k=−∞∑∞x[k]h[n−k]=y[n],n∈Z.(1)
正如你可能猜到的那样,一个无限长信号在实际操作中是不切实际的。此外,在代码中反转 h [ n ] h[n] h[n] 信号中的时间是相当有问题的。因此,我们将做一些假设,然而,这不会改变我们讨论的一般性质。
有限长度信号
我们将假设我们的信号是有限的。当然, h [ n ] h[n] h[n]是这样的,但 x [ n ] x[n] x[n]不一定是如此。
我们用 N x N_x Nx 表示 x [ n ] x[n] x[n] 的长度,用 N h N_h Nh 表示 h [ n ] h[n] h[n] 的长度。
且我们假设 N x > N h N_x \gt N_h Nx>Nh。
对于下标 n < 0 n < 0 n<0 或者 n > = N x n >=N_x n>=Nx,信号都为 0。
反转的滤波器系数
在实际的实时音频场景中,如虚拟现实、计算机游戏或数字音频工作站,我们知道 h [ n ] h[n] h[n] 但不知道 x [ n ] x[n] x[n]
因此,我们可以对
h
[
n
]
h[n]
h[n] 进行反转,我们定义长度为
N
h
N_h
Nh 的 信号
c
c
c 为:
c
[
n
]
=
h
[
N
h
−
n
−
1
]
,
n
=
0
,
…
,
N
h
−
1
(2)
c[n]=h\left[N_{h}-n-1\right], \quad n=0, \ldots, N_{h}-1 \tag{2}
c[n]=h[Nh−n−1],n=0,…,Nh−1(2)
实际的卷积公式
引入上述两个假设后,我们可以将公式(1)改写为:
y
[
n
]
=
(
x
[
n
]
∗
h
[
n
]
)
[
n
]
=
∑
k
=
0
N
h
−
1
x
[
n
+
k
]
c
[
k
]
,
n
=
0
,
…
,
N
x
−
1.
(3)
\begin{array}{c} y[n]=(x[n] * h[n])[n] \\ =\sum_{k=0}^{N_{h}-1} x[n+k] c[k], \quad n=0, \ldots, N_{x}-1 . \end{array} \tag{3}
y[n]=(x[n]∗h[n])[n]=∑k=0Nh−1x[n+k]c[k],n=0,…,Nx−1.(3)
这个公式与相关公式非常相似,但请记住,它仍然是卷积,尽管写法不同。
在这个新的公式中,一个卷积输出只是向量 c c c 和 x x x 的内积。
注意公式(3)的卷积使用的是 “same” 模式,如果我们往 x x x 中追加 N h − 1 N_h-1 Nh−1个0的话,那就变成了 “full” 模式。
正如你将看到的,full 模式将大大简化我们的讨论。
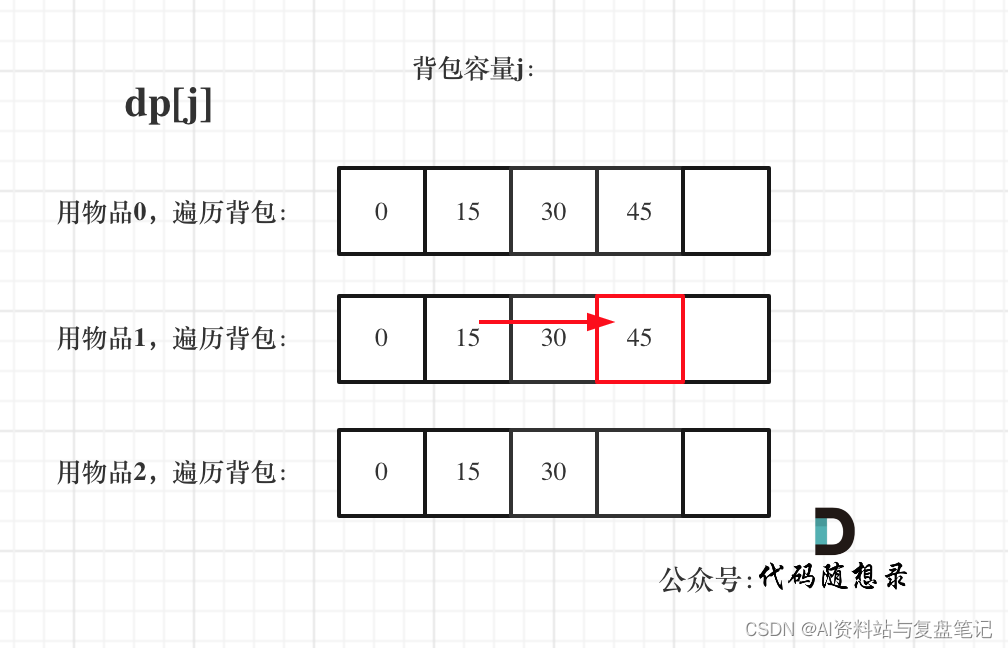
卷积过程可视化
下图说明了卷积是如何计算的。
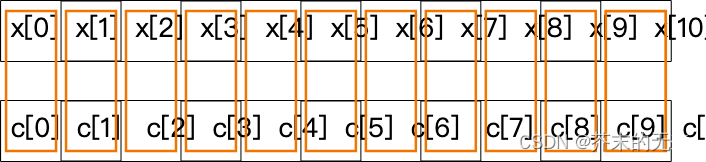
橙色的框框表明哪些元素进行相乘,然后将乘法的结果累加得到
y
[
0
]
y[0]
y[0]
有了上面的假设和卷积格式,我们可以写出它的实现。
线性卷积最简单的实现
在我们用 SIMD 提高 FIR 滤波器的速度之前,我们需要从一个基线开始:一个非 SIMD 的实现。
这可以通过以下方式实现:
struct FilterInput {
// assume that these fields are correctly initialized
const float* x; // input signal with (N_h-1) zeros appended
size_t inputLength; // N_x
const float* c; // reversed filter coefficients
size_t filterLength; // N_h
float* y; // output (filtered) signal;
// pointer to preallocated, uninitialized memory
size_t outputLength; // should be N_x in our context
};
float* applyFirFilterSingle(FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
for (auto i = 0u; i < input.outputLength; ++i) {
y[i] = 0.f;
for (auto j = 0u; j < input.filterLength; ++j) {
y[i] += x[i + j] * c[j];
}
}
return y;
}
正如你所看到的,这段代码的效率不高;我们一个一个地迭代样本。
它的算法时间复杂度是 O ( N h N x ) O(N_hN_x) O(NhNx),让我们来看看如何对这份代码进行向量化。
循环向量化
FIR 滤波器场景下,有 3 中类型的循环向量化方法:
- Inner loop vectorization (VIL),
- Outer loop vectorization (VOL),
- Outer and inner loop vectorization (VOIL).
它们的名字指明了我们将在哪一行将数据加载到 SIMD 寄存器中。其中最容易理解是 VIL
Inner loop vectorization (VIL)
在 VIL 中,我们将在内循环中进行向量化操作。
我们首先以一种粗略的方式来重写之前的代码。我们假设我们的向量长度为 4,这将对应于可以容纳 4 个浮点的寄存器(例如ARM的Neon寄存器)。
float* applyFirFilterInnerLoopVectorization(
FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
for (auto i = 0u; i < input.outputLength; ++i) {
y[i] = 0.f;
// Note the increment by 4
for (auto j = 0u; j < input.filterLength; j += 4) {
y[i] += x[i + j] * c[j] +
x[i + j + 1] * c[j + 1] +
x[i + j + 2] * c[j + 2] +
x[i + j + 3] * c[j + 3];
}
}
return y;
}
上述代码中,在内循环的每一次迭代中,我们做两个 4 元素向量的内积。就这样,我们计算出公式(3)中卷积和的一部分。
请注意,我们假设传入的向量已经是零填充的,并且长度是4的倍数。
下图显示了 VIL 的情况
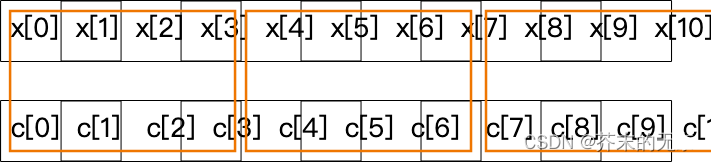
当然,这份代码并不比之前的代码更优化。它只是以向量形式重写了代码。但这种向量形式现在很容易用向量指令来实现。
这个实现在真正的SIMD代码中看起来如何呢?
VIL NEON 实现
下面我将使用 NEON intrinsic 函数来实现 VIL。NEON 相关教程请参考Neon intrinsics 简明教程。
#ifdef __aarch64__
float* applyFirFilterInnerLoopVectorizationARM(FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
assert(input.inputLength % 4 == 0);
assert(input.filterLength % 4 == 0);
for (auto i = 0u; i < input.outputLength; ++i) {
y[i] = 0.f;
float32x4_t outChunk = vdupq_n_f32(0.0f);
for (auto j = 0u; j < input.filterLength; j += 4) {
float32x4_t xChunk = vld1q_f32(x + i + j);
float32x4_t cChunk = vld1q_f32(c + j);
float32x4_t temp = vmulq_f32(xChunk, cChunk);
outChunk = vaddq_f32(outChunk, temp);
}
y[i] = vaddvq_f32(outChunk);
}
return y;
}
#endif
同样,我们假设传入的向量已经是零填充,并且长度是4的倍数.
其算法时间复杂度是 O ( N x N h / 4 ) O(N_xN_h/4) O(NxNh/4)。当然,在复杂性理论中,这和非向量化算法是一样的。但是请注意,在内循环中,我们的迭代次数减少了 4 倍。这是因为我们可以用单条 NEON 指令对 4 个浮点数的向量进行操作。
Outer Loop Vectorization (VOL)
VOL 是一个更疯狂的方法。在这种方法中,我们试图在一次外循环中一次性计算出一个输出的向量。同样地,我们先给出粗略的 VOL 代码实现
float* applyFirFilterOuterLoopVectorization(
FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
// Note the increment by 4
for (auto i = 0u; i < input.outputLength; i += 4) {
y[i] = 0.f;
y[i + 1] = 0.f;
y[i + 2] = 0.f;
y[i + 3] = 0.f;
for (auto j = 0u; j < input.filterLength; ++j) {
y[i] += x[i + j] * c[j];
y[i + 1] += x[i + j + 1] * c[j];
y[i + 2] += x[i + j + 2] * c[j];
y[i + 3] += x[i + j + 3] * c[j];
}
}
return y;
}
同样,我们假设传入的向量已经是零填充的,并且长度是4的倍数。
下图显示了 VOL 的情况
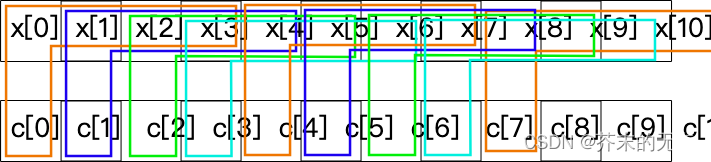
我们不是在内循环中从卷积和中计算4个元素(如VIL),而是从4个卷积和中计算1个元素。在VIL中,我们的内循环迭代次数减少了4次,在VOL中,我们的外循环迭代次数减少了4次。
因此,VOL并不比VIL更优化。
这个代码现在很容易用SIMD指令来实现。
VOL NEON Implementation
下面代码说明了如何使用 NEON 实现 VOL
float* applyFirFilterOuterLoopVectorizationARM(FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
// Note the increment by 4
for (auto i = 0u; i < input.outputLength; i += 4) {
float32x4_t yChunk{0.0f, 0.0f, 0.0f, 0.0f};
for (auto j = 0u; j < input.filterLength; ++j) {
float32x4_t xChunk = vld1q_f32(x + i + j);
float32x4_t temp = vmulq_n_f32(xChunk, c[j]);
yChunk = vaddq_f32(yChunk, temp);
}
// store to memory
vst1q_f32(y + i, yChunk);
}
return y;
}
这段代码应该比最初的代码快 4 倍。在实践中,由于额外的代码,速度提升会更小。
一个问题出现了:我们可以做得更好吗?是的,我们可以!
Outer and Inner Loop vectorization (VOIL)
真正的突破来自于我们结合两种类型的矢量化。
在这种方法中,我们在外循环中计算一个向量,在内循环中使用向量内积,粗略的代码如下:
float* applyFirFilterOuterInnerLoopVectorization(
FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
// Note the increment
for (auto i = 0u; i < input.outputLength; i += 4) {
y[i] = 0.f;
y[i + 1] = 0.f;
y[i + 2] = 0.f;
y[i + 3] = 0.f;
// Note the increment
for (auto j = 0u; j < input.filterLength; j += 4) {
y[i] += x[i + j] * c[j] +
x[i + j + 1] * c[j + 1] +
x[i + j + 2] * c[j + 2] +
x[i + j + 3] * c[j + 3];
y[i + 1] += x[i + j + 1] * c[j] +
x[i + j + 2] * c[j + 1] +
x[i + j + 3] * c[j + 2] +
x[i + j + 4] * c[j + 3];
y[i + 2] += x[i + j + 2] * c[j] +
x[i + j + 3] * c[j + 1] +
x[i + j + 4] * c[j + 2] +
x[i + j + 5] * c[j + 3];
y[i + 3] += x[i + j + 3] * c[j] +
x[i + j + 4] * c[j + 1] +
x[i + j + 5] * c[j + 2] +
x[i + j + 6] * c[j + 3];
}
}
return y;
}
为什么 VOIL 更优?
你可能会对自己说 “好吧,但这只是一个手动展开的循环! 为什么它更快?”。
这是因为 SIMD 指令同时使用多个寄存器,如VOIL情况下,为处理器提供了更多的空间,可以更快地执行它们。这与 VIL 或 VOL 情况下只使用一个或两个寄存器形成对比。
当我说 "同时 "时,我并不是指多线程。我的意思是保持对各种寄存器的引用。这使处理器能够最有效地处理事情。
数据对齐
VOIL有如此大的优化潜力的另一个原因是,我们可以使用对齐的加载/存储SIMD指令来实现它。如何实现?这将是下一篇文章的主题!
让我们看看如何用 NEON 指令实现 VOIL。
VOIL NEON Implementation
float* applyFirFilterOuterInnerLoopVectorizationARM(FilterInput& input) {
const auto* x = input.x;
const auto* c = input.c;
auto* y = input.y;
std::array<float32x4_t, 4> outChunk{};
for (auto i = 0u; i < input.outputLength; i += 4) {
for(auto k = 0; k < 4; ++k){
outChunk[k] = vdupq_n_f32(0.0f);
}
for (auto j = 0u; j < input.filterLength; j += 4) {
float32x4_t cChunk = vld1q_f32(c + j);
for(auto k = 0; k < 4; ++k)
{
float32x4_t xChunk = vld1q_f32(x + i + j +k);
float32x4_t temp = vmulq_f32(cChunk, xChunk);
outChunk[k] = vaddq_f32(temp, outChunk[k]);
}
}
for(auto k = 0; k < 4; ++k){
y[i + k] = vaddvq_f32(outChunk[k]);
}
}
return y;
}
总结
在这篇文章中,我们讨论了什么是FIR滤波器以及如何有效地实现它;要么选择快速卷积算法,要么使用现代处理器的单指令、多数据指令。当然,你可以两者兼得
我们重新定义了卷积和,以方便讨论和实现。
我们研究了使用一种叫做循环矢量化的技术来实现FIR滤波器。我们展示了 VIL、VOL 和 VOIL 的普通C语言实现,讨论了它们的可视化,并使用 NEON 指令集展示了它们的SIMD等价物。
最后,我们指出,我们可以用对齐的数据做得更好。这将在下一篇文章中讨论。
请看看下面的有用的参考资料。整个代码可以在我的GitHub仓库中找到。
和往常一样,如果你有任何问题,请随时在下面发表。
参考
- 【音频处理】Fast Convolution 快速卷积算法简介
- Convolution: The secret behind filtering