题目：纯完全背包问题

题目描述：
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和0-1背包问题唯一不同的地方就是，每种物品有无限件。

同样leetcode上没有纯完全背包问题，都是需要完全背包的各种应用，需要转化成完全背包问题，所以我这里还是以纯完全背包问题进行讲解理论和原理。

在下面的讲解中，我依然举这个例子：

背包最大重量为4。

物品为：
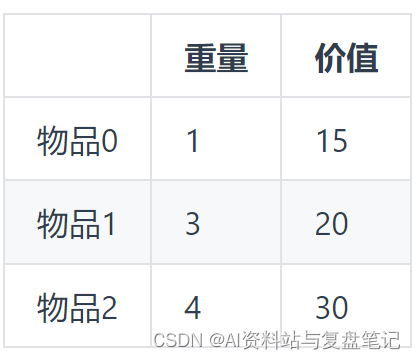
在这里插入图片描述

本题重难点

每件商品都有无限个！

问背包能背的物品最大价值是多少？

0-1背包和完全背包唯一不同就是体现在遍历顺序上，所以本文就不去做动规五部曲了，我们直接针对遍历顺序经行分析！

首先在回顾一下0-1背包的核心代码

for(int i = 0; i < weight.size(); i++) { // 先遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 再遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

我们知道0-1背包内层的循环是从大到小（倒序）遍历，为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的，所以内层的循环要从小到大（正序）去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

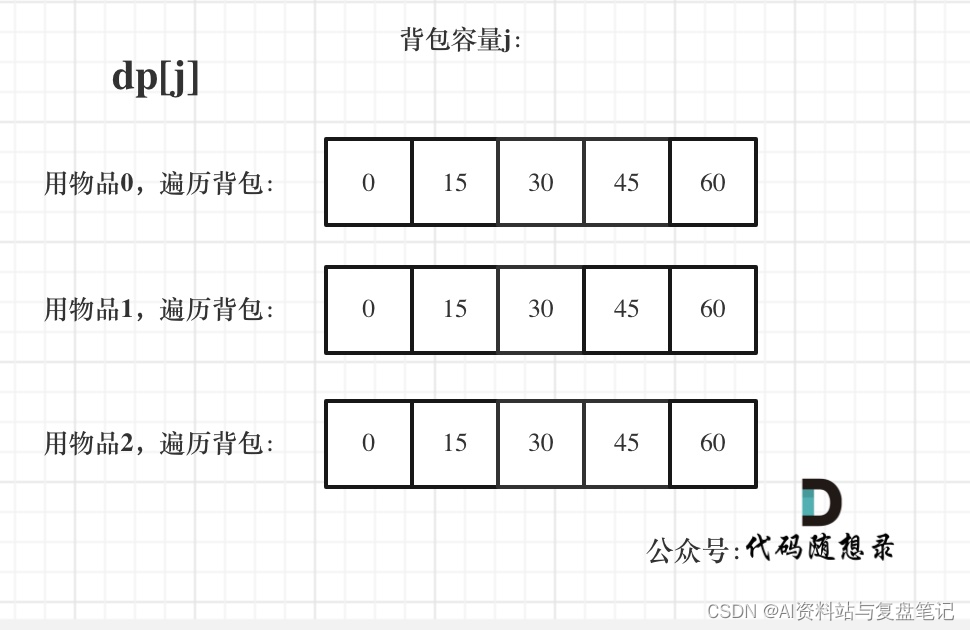
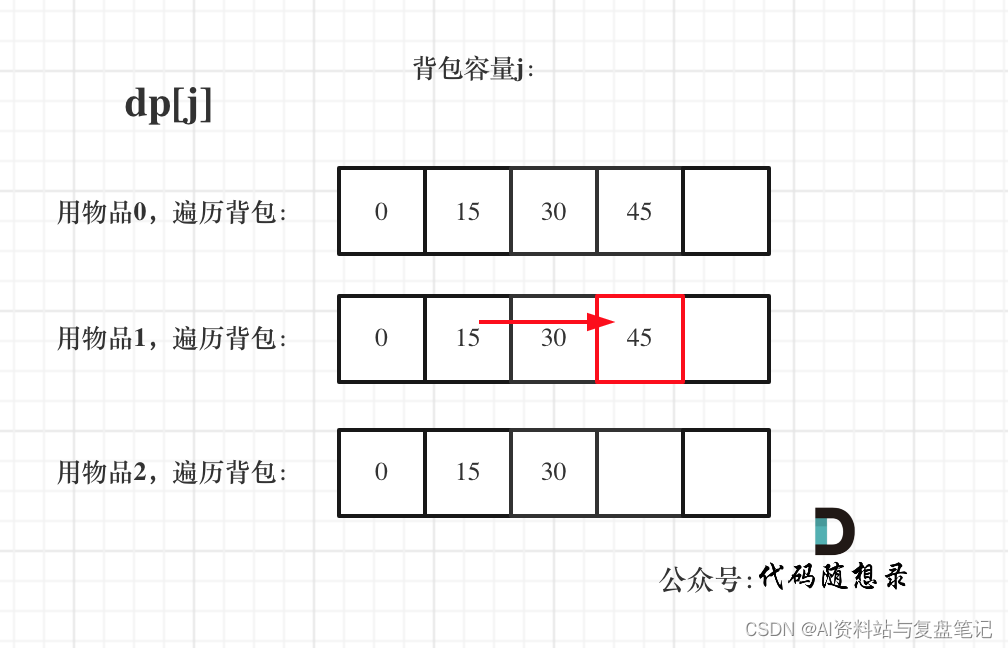
dp状态图如下：

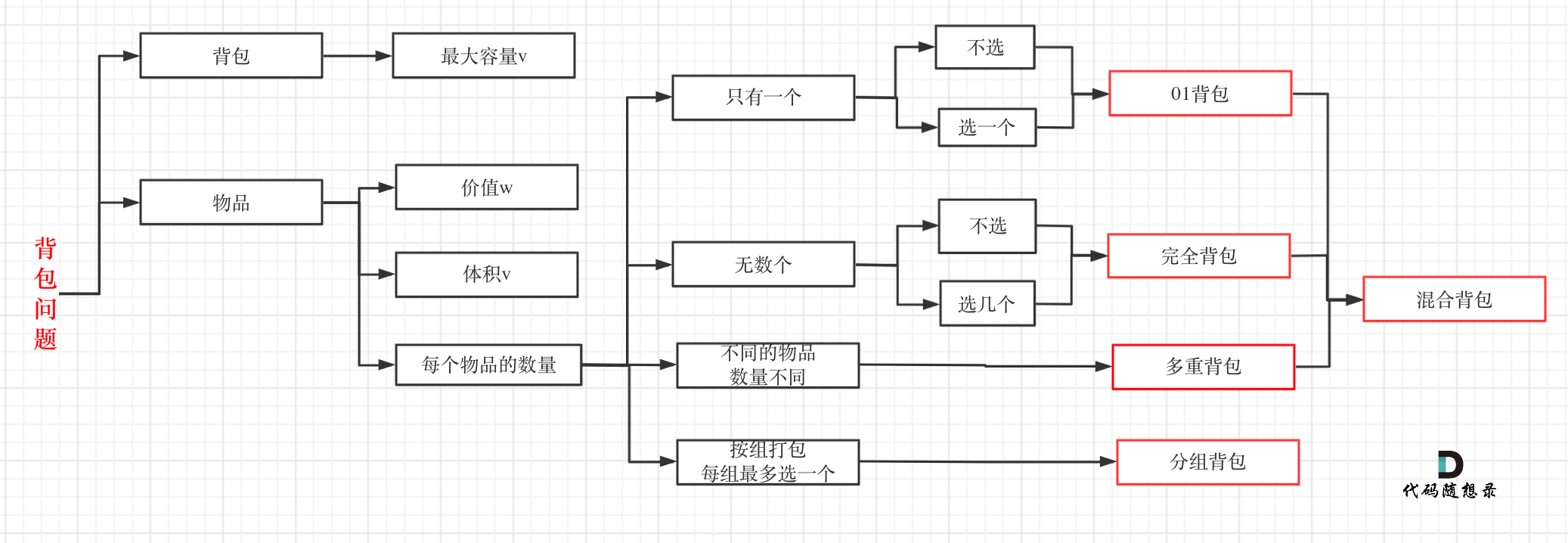
讲完了完全背包的代码之后其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？

在一文搞懂纯0-1背包问题
我们讲过0-1背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的。只要保证下标j之前的dp[j]都是经过计算的就可以了。

遍历物品在外层循环，遍历背包容量在内层循环，状态如图：

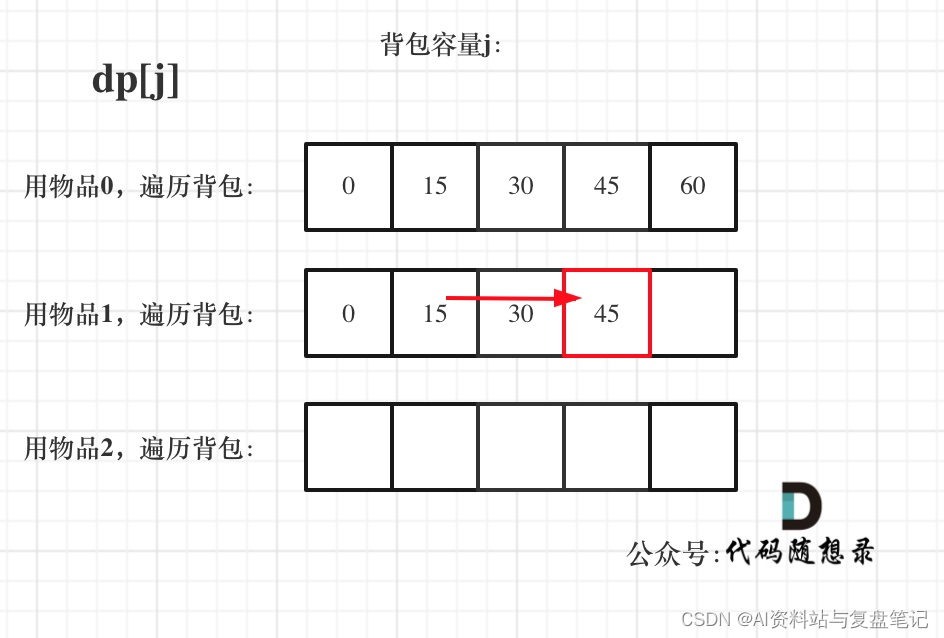
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。

先遍历背包在遍历物品，代码如下：

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}