求解常微分方程 ODE

​ 在matlab中，我们可以求解常微分方程的解析解，和数值解，一般使用dsolve来求解常微分方程的解析解，使用类似于ode45的求解器来求解常微分方程的数值解。

（1）求解解析解

求解解析解，例如求解该方程的解析解
$$\frac{dy}{dx}=3x^2+1$$
只需要在命令行中输入

dsolve('Dy=3*x^2+1', 'x')

或者是加上初始条件，求该方程在该初始条件下的解
$$\frac{dy}{dx}=3x^2,y{|}_{x=0}=2$$
在命令行输入

dsolve("Dy = 3*x^2", "y(0)=2", "x")

例如求一个常微分方程组
$$\{\begin{array}{l}\dot{x}=y,\\ \ddot{y}-\dot{y}=0,x{|}_{t=0}=1;\dot{y}{|}_{t=0}=1\end{array}$$
在命令行输入

[x, y] = dsolve('Dx=y, D2y-Dy=0', 'x(0)=2, y(0)=2, Dy(0)=1')

（2）求解数值解

求数值解，有一些非线性的常微分方程是不能求出解析解的，我们一般求取其在一段区间内的数值解，采用迭代的方式来求解数值解，ode是matlab专门用于解微分方程的功能函数，具体的说明如下：

ode45是解决问题的首选，如果长时间没有结果，那么则采用ode15s试试。下面介绍ode45的函数格式

%函数格式  
%[T,Y] = ode45(‘odefun’,tspan,y0)
%[T,Y] = ode45(‘odefun’,tspan,y0,options)
%[T,Y,TE,YE,IE] = ode45(‘odefun’,tspan,y0,options)
%sol = ode45(‘odefun’,[t0 tf],y0...)
%其中: odefun是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名；
%          tspan 是求解区间 [t0 tf]，或者一系列散点[t0,t1,...,tf]；
%          y0 是初始值向量
%          T 返回列向量的时间点
%          Y 返回对应T的求解列向量
%          options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等
%          TE 事件发生时间
%          YE 事件发生时之答案
%          IE 事件函数消失时之指针i

首先得将微分方程标准化，类似于选择状态变量写状态空间表达式，对于一般的微分方程

$$\{\begin{array}{l}F(y,\dot{y},\ddot{y},\dots ,y^{(n-1)},t)=0\\ y(t_0)=c_0,\dot{y}(t)=c_1,\dots ,y^{(n-1)}(t_0)=c_{n-1}\end{array}$$

首先选择选择一组微分作为状态变量

$$\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}y\\ \dot{y}\\ \ddot{y}\\ ⋮\\ y^{(n-1)}\end{array}\right]$$

然后将待求解的微分方程$F(y,\dot{y},\ddot{y},\dots ,y^{(n-1)},y^n,t)=0$，写成$y^n=G(y,\dot{y},\ddot{y}\dots ,y^{n-1},t)=G(x_1,x_2,x_3\dots ,x_n,t)$的形式，然后写出$\dot{\mathbf{x}}$

$$\dot{\mathbf{x}}=\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\\ \dot{x_3}\\ ⋮\\ \dot{x_n}\end{array}\right]=\left[\begin{array}{c}\dot{y}\\ \ddot{y}\\ ⋮\\ y^{(n-1)}\\ y^{(n)}\end{array}\right]=\left[\begin{array}{c}{x}_2\\ x_3\\ x_4\\ ⋮\\ G(x_1,x_2,x_3\dots ,x_n,t)\end{array}\right]$$

上述步骤便是我们需要在odefun中完成的，举一个示例：在时间区间$t=[3.9,4]$，求解微分方程

$$y^{\prime \prime }=-ty+e^t{y}^{\prime }+3sin2t,y{|}_{t=3}=8,y^{\prime }{|}_{t=3}=2$$
那么即
$$\dot{\mathbf{x}}=\left[\begin{array}{c}\mathbf{x}[1]\\ -t\ast \mathbf{x}[1]+e^t\ast \mathbf{x}[2]+3sin2t\end{array}\right]$$

%在odefun.m脚本文件中完成以下内容
function dxdt = odefun(t, x)
	dxdt = zeros(2, 1);  %初始化为 2 x 1的零矩阵
	dxdt(1) = x(2);
	dxdt(2) = -t*x(1)+exp(t)*x(2)+3*sin(2*t);
end

%在main.m脚本文件中完成以下内容
tspan = [3.9, 4];
y0 = [8, 2];
[t, y] = ode45('odefun', tspan, y0);	%x的第一列为y，第二列为y’。如果遇到变量不是列向量形式的，可以考虑利用reshape函数做矩阵变换。
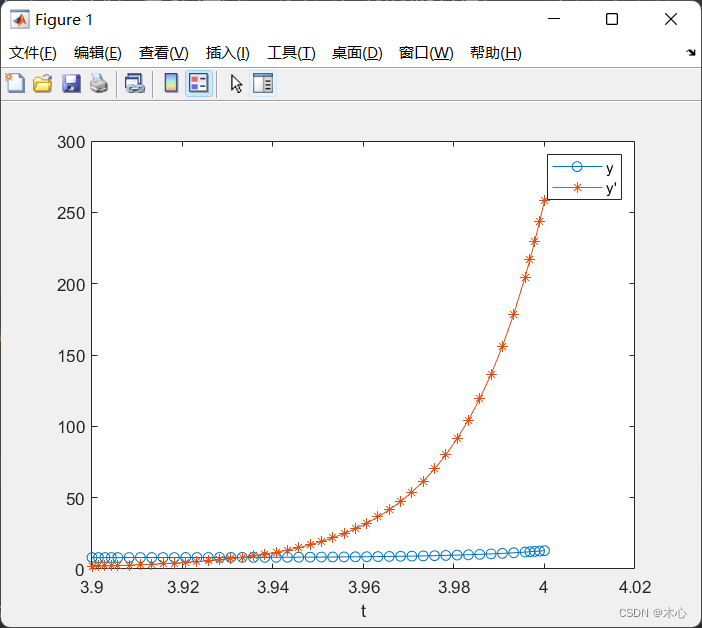
plot(t, y(:,1), '-o', t, y(:,2), '-*');
legend('y', "y'");
xlabel('t');