最小二乘定权、电离层对流层改正，都需要卫星的高度角、方位角。本章将介绍求解完卫星的地固坐标系的位置后，如何求解卫星的高度角、方位角。

    卫星位置求解请参考之前的博客：卫星位置解算原理与程序设计

参考书籍：黄丁发，熊永良，周乐韬等，GPS卫星导航定位技术与方法，科学出版社。

目录

公式原理

程序设计（C语言）

---

公式原理

    站心坐标系也称NEU坐标系或东北高坐标系，在地球上任一点观测卫星时，最直观和最方便的办法是知道卫星所在的瞬时位置的方位和仰角。因此，需将卫星的地固坐标系转化成站心坐标系。 

    站心直角坐标系是以测站为坐标原点的左手坐标系，其N轴指向过该测站的子午线，北向为正；U轴重合与该点上WGS84椭球法线，向外为正；E轴位于该点的切平面，东向为正，如下图所示： 

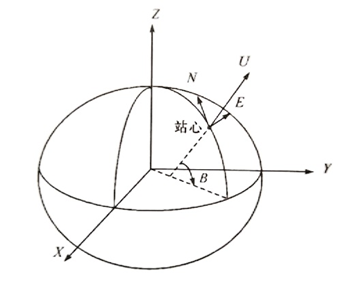
     站心坐标系常用极坐标表示（方位角A、高度角h、向径r），如下图所示：

    建立以已知测站点为原点的站心直角坐标系，则卫星在该坐标系的坐标为：

式中：为卫星在地固系中的坐标向量；为测站在地固坐标系中的坐标向量；为卫星在站心坐标系中的坐标向量；R为旋转矩阵，即： 

 式中：B,L为测站的大地维度和大地精度。

    卫星从站心直角坐标系转换到站心极坐标系的公式为：

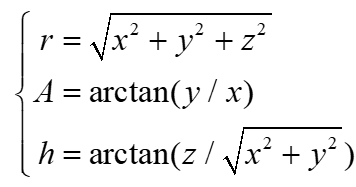
式中：r为卫星向径，A为卫星方位角，h为卫星的高度角。

    卫星从站心极坐标系转到站心直角坐标系的公式为：

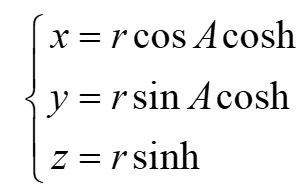
程序设计（C语言）

根据上述公式，求解卫星的站心极坐标需要8个参数：卫星地固坐标系xyz，测站地固坐标系xyz，以及测站经纬度BL（B表示维度，L表示经度）。

#define PI 3.141592653589793

//计算卫星高度角(弧度)
RAH satrah(double Xr, double Yr, double Zr, double Xs, double Ys, double Zs, double Lr, double Br)
{
	RAH rah = { 0 };
	int i;
	double** R, ** X, ** res;
	R = (double**)malloc(sizeof(double*) * 3);
	X = (double**)malloc(sizeof(double*) * 3);
	res = (double**)malloc(sizeof(double*) * 3);
	if (R)
	{
		for (i = 0; i < 3; i++)
		{
			R[i] = (double*)malloc(sizeof(double) * 3);
			X[i] = (double*)malloc(sizeof(double) * 1);
			res[i] = (double*)malloc(sizeof(double) * 3);
		}
	}
	//构建旋转矩阵R
	R[0][0] = -sin(Lr);
	R[0][1] = cos(Lr);
	R[0][2] = 0;
	R[1][0] = -sin(Br) * cos(Lr);
	R[1][1] = -sin(Br) * sin(Lr);
	R[1][2] = cos(Br);
	R[2][0] = cos(Br) * cos(Lr);
	R[2][1] = cos(Br) * sin(Lr);
	R[2][2] = sin(Br);
	//构建X向量
	X[0][0] = Xs - Xr;
	X[1][0] = Ys - Yr;
	X[2][0] = Zs - Zr;
	res = Matrix_Mul(R, X);
	rah.h = atan2(res[2][0],sqrt(pow(res[0][0], 2) + pow(res[1][0], 2)));
	if (rah.h < 0)
		rah.h += PI / 2;
	rah.A = atan2(res[1][0], res[0][0]);
	if (rah.A < 0)
		rah.A += 2*PI;
	if (rah.A > 2 * PI)
		rah.A -= 2*PI;
	rah.r = sqrt(pow(res[0][0], 2) + pow(res[1][0], 2) + pow(res[2][0], 2));
	free(R);
	free(X);
	free(res);
	return rah;
}

1）RAH为用于传参的结构体，代码如下：

//卫星极坐标函数传参
typedef struct RAH
{
	double r;
	double A;
	double h;
}RAH;

2）Matrix_Mul为自行编写的矩阵乘法函数，具体代码请见C语言矩阵乘法

3）atan2为四象限反正切函数（atan，atan2并不相同），三角函数单位均为弧度

4）高度角h范围在0~90°；若高度角h＜0，h=h+pi

5）方位角A范围在0~360°；若A＜0，A=A+2pi；若A＞2pi，A=A-2pi

6）务必释放内存！