---

摘要

This week, I read a paper on Recurrent Reural Networks that proposed a new recurrent reural network architecture that achieves functionality comparable to LSTM and GRU in a simplified structure. Compared with LSTM and GRU, this network architecture has the least amount of parameter update, which is conducive to efficient training and testing. More importantly, it has better interpretability and trainability. In the learning of Recurrent Neural Network, I simply learn the variant models of RNN, LSTM and GRU, which can solve the problems of gradient vanshing and gradient explode in the process of long sequence training encountered by RNN. In addition, I summarize some simple understandings of tensor, gradient, divergence and curl, and prove the identities in vector analysis using tensor.

本周，我阅读了一篇关于循环神经网络的论文，论文中提出了一种新的循环神经网络架构，它以简化的结构实现了与LSTM和GRU相当的功能。这种网络架构比LSTM和GRU有着最少的参数更新量，有利于高效的训练和测试，更重要的是它具有更好的可解释性和可训练性。在循环神经网络的学习中，我简单地学习了RNN的变体模型LSTM和GRU，它们能够解决RNN遇到的长序列训练过程中的梯度消失和梯度爆炸问题。此外，我还总结了一些对张量、梯度、散度和旋度的简单理解，并利用张量证明了矢量分析中的恒等式。

---

文献阅读

1.题目

文献链接：MinimalRNN: Toward More Interpretable and Trainable Recurrent Neural Networks

2.摘要

We introduce MinimalRNN, a new recurrent neural network architecture that achieves comparable performance as the popular gated RNNs with a simplified structure. It employs minimal updates within RNN, which not only leads to efficient learning and testing but more importantly better interpretability and trainability. We demonstrate that by endorsing the more restrictive update rule, MinimalRNN learns disentangled RNN states. We further examine the learning dynamics of different RNN structures using input-output Jacobians, and show that MinimalRNN is able to capture longer range dependencies than existing RNN architectures.

3.介绍

RNN已经广泛应用于各个领域的序列数据建模，其中LSTM和GRU是最突出的模型，尽管它们的性能优异，但由于这些模型的内在复杂性使我们无法彻底了解它们的优势，以至于存在局限性。因此，论文对现有RNN模型的问题进行了改良设计，在不损失性能的同时进一步缓解了梯度消失问题，增强了内部神经元的可解释性。

现有RNN存在的一个问题是对于噪声扰动过于敏感，不够稳健。初始状态的轻微扰动都会造成后续结果的巨大变化，为此论文中提到Chaos Free Networks (CFN)可以试图解决这一问题。因此，CFN的做法是将循环部分的矩阵相乘换成element-wise product，
以GRU为例：

修改为：

其中的思想是每一个神经元在各个时间步t之间应当保持独立性，这样可以增强内部神经元的可解释性，而现有的矩阵相乘是通过全连接联系ht和ht+1，这样隐状态h下一时刻的每一个神经元除了和自身关联，还会和其它神经元有权重关联。受到CFN成功的启发，论文中提出更简单的RNN结构MinimalRNN，它简单不牺牲性能，不仅带来了效率，还带来了可解释性和可训练性。

4.方法

如下图所示，这是论文中提出更简单的RNN结构：MinimalRNN的模型架构图

Ф(x)将输入x映射到zt，使得zt和隐状态ht在同一个空间中，这样它们就能在上图中第三个式子通过相加操作来更新隐状态，其中的ut是门，作用相当于缩放操作。原因是在同一个空间中的两个向量相加才有明晰的意义，不在同一空间的话我们认为没有意义，或者说我们不好说清楚它有什么意义。相较于传统的LSTM或GRU，这个结构要简单许多，无论是参数数量还是计算复杂度上有具有优势。

5.实验

目标：考虑到用户使用系统中项目的历史情况下，向用户推荐感兴趣的项目。

5.1 数据集

数据集包含数以亿计的用户记录，记录用户使用推荐项目的上下文。论文中考虑了长达数月的用户活动，并将序列截断最大长度设为500，项目词汇表包含了过去48小时内500万个最受欢迎的项目。

5.2 网络模型

论文采用GRU模型，用于捕捉随时间演变的用户兴趣。

5.3 实验表现

从图中信息可以看出，VanillaRNN在学习的早期阶段由于梯度爆炸而导致出现失败情况，在其他三种模型的比较中，由于MinimalRNN的更新要简单得多，因此训练所需的时间更少，大概在30小时内完成，而CFN需要36小时，GRU需要46小时。因此，MinimalRNN的表现比其他几个模型更好。

6.展望

论文中较为简单的循环神经网络架构能否执行除论文中所述任务之外的广泛任务，还有待观察。因为针对论文中的任务最有效的模型仅使用一个全连接层，而面对更为复杂的输入时，我们就需要增加模型的深度来寻找更为有效的方法去解决问题。

深度学习

LSTM参考链接：https://www.cnblogs.com/luyizhou/p/15469779.html
GRU参考链接：https://blog.51cto.com/u_15127545/4367220
张量参考链接：https://zhuanlan.zhihu.com/p/121429834

1.LSTM原理

1.1 什么是LSTM？

LSTM是一种特殊的RNN，主要的作用是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，相比于普通的RNN，LSTM能够在更长的序列中有更好的表现。

将上图拆分理解：
1）如果没有门结构，细胞的状态类似于输送带，细胞的状态在整个链上运行，只有一些线性函数作用，信息很容易保持不变的流过整个链。
2）门(gate)是一种可选地址信息通过的方式， 它由一个Sigmoid神经网络层和一个点乘法运算组成。简单来说，就是对数据进行运算操作，而对运算后的数据信息是否处理需要靠gate来判断。Sigmoid神经网络层输出范围为0到1之间的数字，它表示每个组件有多少信息可以通过， 0表示不通过任何信息，1表示全部通过。
3）LSTM有三个gate，用于保护和控制细胞的状态。

1.2 遗忘门（forget gate）

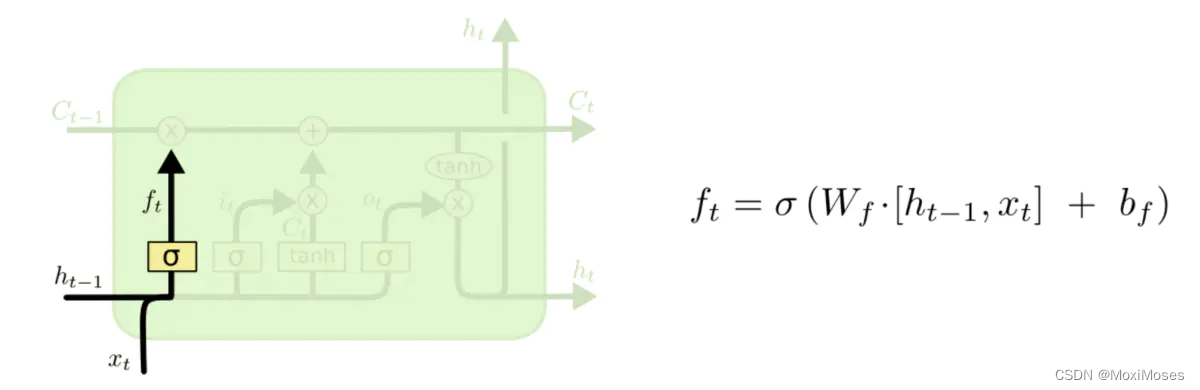
遗忘门的作用是决定神经网络需要丢弃哪些不重要的信息，此操作由遗忘门的Sigmoid层实现。
可训练参数：Wf ，bf 参数矩阵

1.3 输入门（input gate）

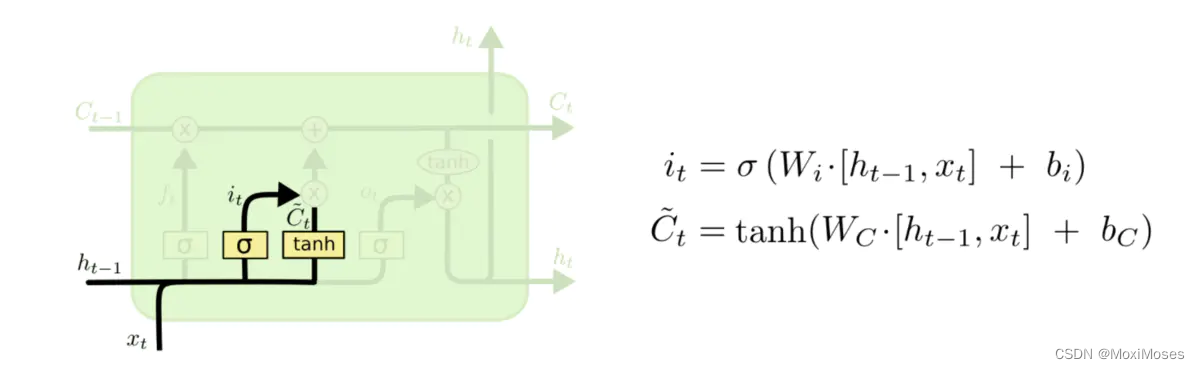
输入门的作用是决定神经网络需要存储哪些信息，此部分分为两个步骤：
1）输入门的sigmoid神经网络层决定了应不应该更新数据或者以多大的比例去更新数据。
2）输入门的tanh神经网络层生成了一个加入到细胞态的候选向量Ct。
于是，将上面两个步骤的结果向量进行点乘，最终确定如何去更新细胞态。
可训练参数：Wi，bi，Wc，bc参数矩阵

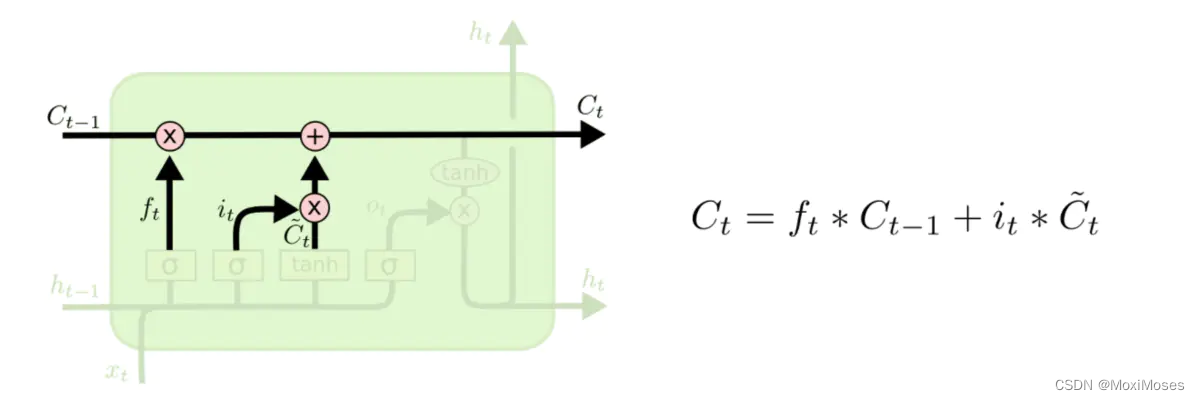
上图为Ct的更新公式，清晰地说明了遗忘门和输入门是如何对长期、短期的信息来实现遗忘和记忆的。
可训练参数：无

1.4 输出门（output gate）

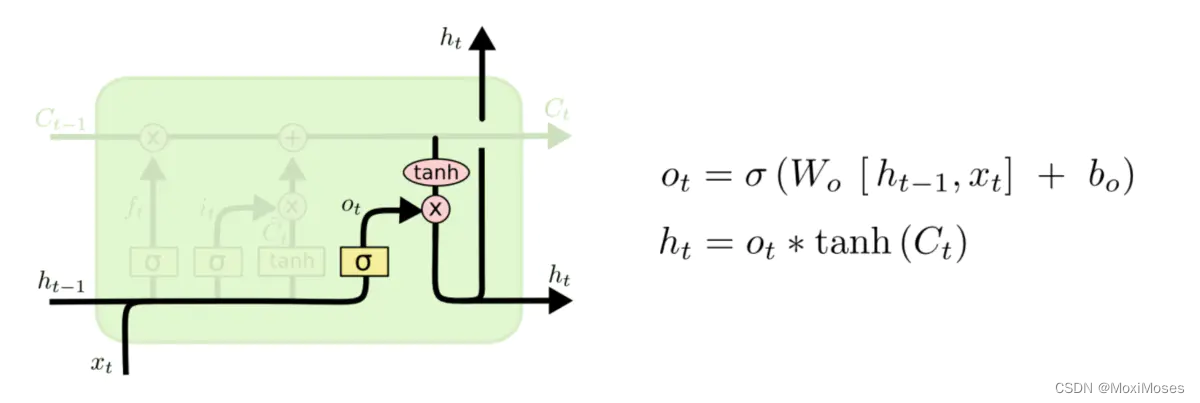
输出门的作用是决定神经网络输出哪些信息。首先通过输出门的sigmoid层决定输出信息，然后将Ct通过tanh层将值规范化到-1和1之间，并将其乘以Sigmoid门的输出，此时得到的结果为最终要输出的结果ht。
可训练参数：Wo，bo 参数矩阵。

2.GRU原理

GRU是LSTM一个效果不错的变体网络，它较于LSTM的结构更为简单，也能够解决RNN遇到的长依赖问题。

GRU的特点是参数数量较少，训练速度快，能够降低过拟合的风险。对比于LSTM引入3个gate：遗忘门、输入门和输出门，GRU只有两个gate：更新门和重置门。

GRU具体结构如下图所示：

其中：zt表示更新门，rt表示重置门。
更新门用于控制前一时刻的状态信息被带入到当前状态中的程度，更新门的值越大说明前一时刻的状态信息带入量越多。
重置门控制前一状态有多少信息被写入到当前的候选集上，重置门越小，前一状态的信息被写入量越少。

3.LSTM与GRU的比较

1）GRU相比于LSTM少了一个输出门，则GRU的参数量比LSTM少。
2）对于某些较小的数据集上，GRU相比于LSTM能够表现出更好的性能。
3）从严格意义上来说，LSTM比GRU更强，因为它可以很容易地进行无限计数，这也是LSTM能够学习简单语言的原因。

4.张量

张量：不依赖坐标系来反应物质的一个物理量。

标量：一个0阶张量
矢量：一个1阶张量
有人说矩阵是一个张量，但是从严格意义来说，它不是一个张量，因为一个张量由一个数（张量的分量）和基矢量的并矢组成，而这个数也可以是一个矩阵，因此我们可以用一个矩阵唯一的代表一个张量。
并矢：当我们把一个m阶张量和一个n阶张量做并矢，就会得到一个m+n阶的张量，因此并矢是一个升阶的过程。

5.梯度、散度和旋度

梯度：在某个场中，某点某物理参数增加最快的方向
散度：矢量场发散的程度
旋度：矢量场对于某一点附近的旋转程度

其中有两个公式需要记忆：
1）梯度的旋度是0，理解为一个发散的场不会旋转。
2）旋度的散度是0，理解为一个旋转的场不会发散。

6.利用张量证明矢量分析中的恒等式

7.将任意一个波函数，通过差分推导写成RNN结构

---

总结

在本周的学习中，我继续学习了循环神经网络方面的内容，对于RNN面临的长期依赖问题（由于反向传播存在的梯度消失或爆炸问题，简单RNN很难建模长距离的依赖关系），一种比较有效的方案是在RNN基础上引入门控机制来控制信息的传播，因此LSTM和GRU得到了广泛的使用。在下周的学习中，我们深入地学习LSTM和GRU，掌握其中的原理。