一、Dijkstra算法

Dijkstra算法与之前学习过的Prim算法有些相似之处。我们直接通过一个例子来讲解

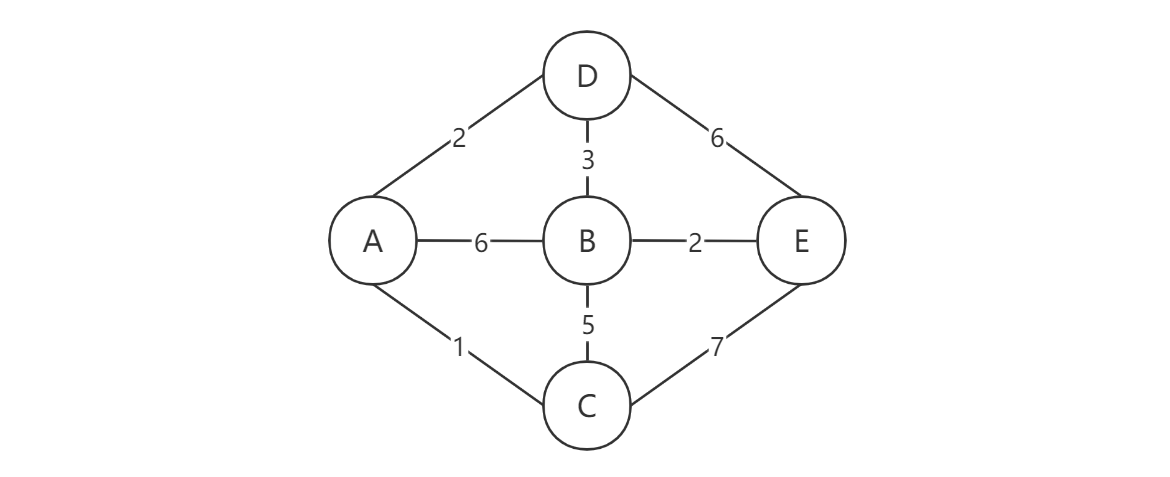
假设要求的是A->E之间的最短路径。首先我们来列出顶点A到其他各顶点的路径长度：A->D = 2，A->B = 6，A->C = 1，A->E = ∞。既然是要寻找最短路径，我们当然是先在已有的路径里面挑一条最短的，也就是A->C。将到达过的顶点用红色进行标识

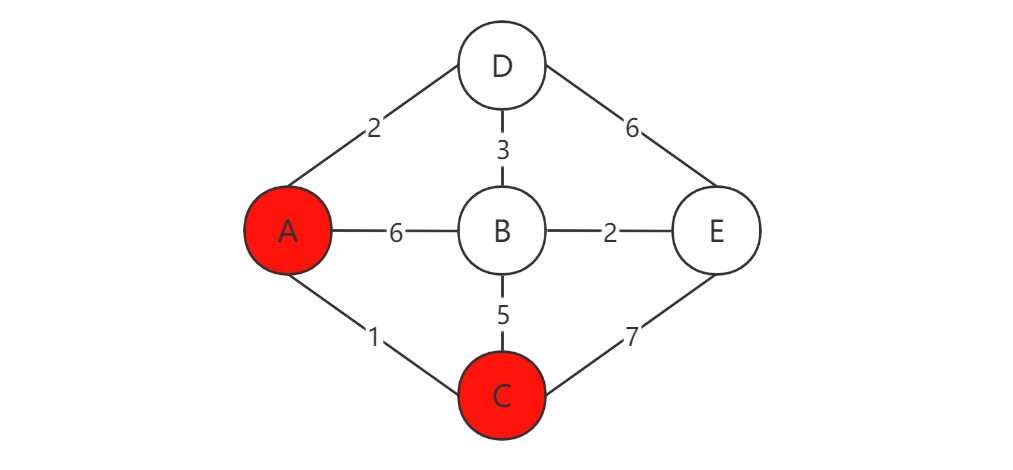
到达C点后，我们又可以找到两条路径：C->B = 5，C->E = 7。此时我们拿这几条新的路径长度，与之前的A->C = 1相加，就可以得到A->B = 6，A->E = 8。出现了一条比之前短的路径：A->E = 8。所以我们将其更新到之前的路径列表里：A->D = 2，A->B = 6，A->C = 1，A->E = 8。

接下来再从路径列表里选择一条最短的路径，也就是：A->D = 2。将D标记为已到达。

到达D点后，又可以找到两条新的路径：D->B = 3，D->E = 6。与A->D = 2相加可得：A->B = 5，A-E = 8。又有一条比之前短的路径：A->B = 5，所以将其更新到路径列表：A->D = 2，A->B = 5，A->C = 1，A->E = 8。

再选择一条最短的路径：A->B = 5。将B标记为已到达。

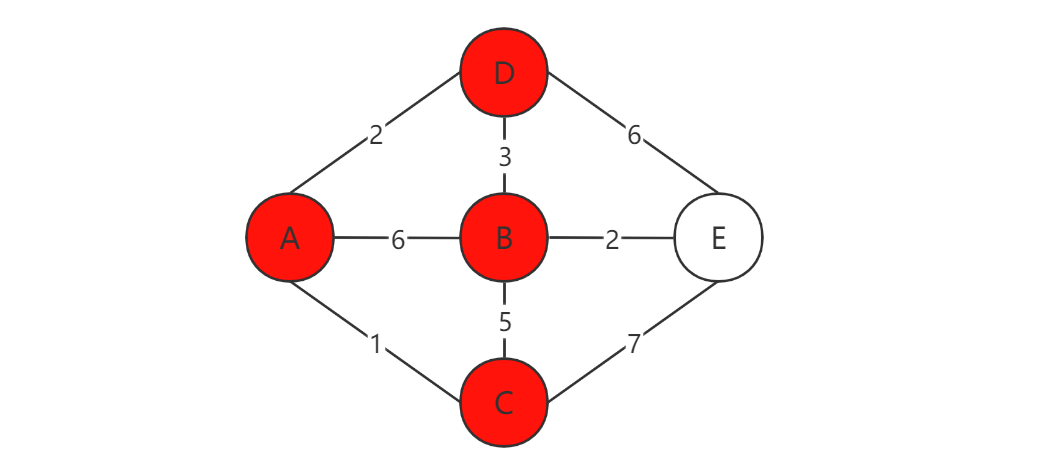
这次只有一条新的路径：B->E = 2。将其与A->B = 5相加得：A->E = 7。比之前的路径更短，所以更新到路径列表：A->D = 2，A->B = 5，A->C = 1，A->E = 7。最后来到E点，结束遍历。

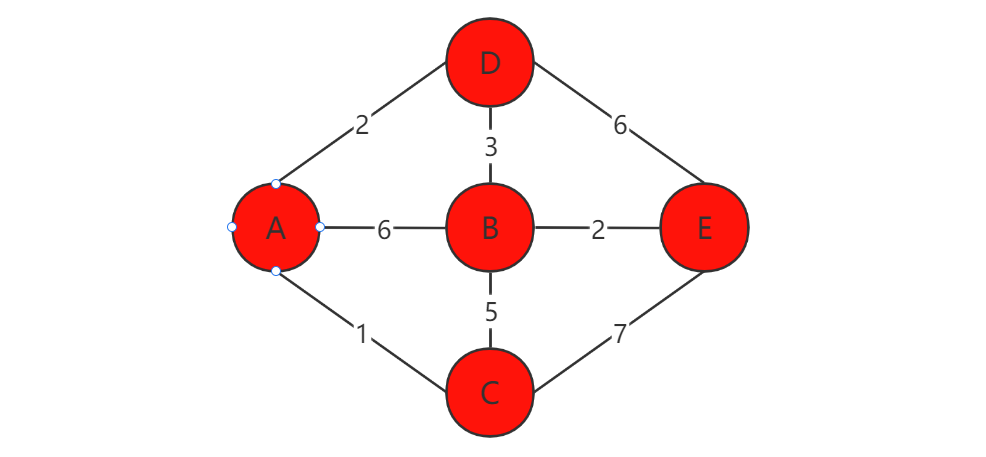
与此同时，我们获得了一张从A到各个顶点的最短路径长度表。

代码如下

public struct Path
{
	// 上一顶点下标
	public int preNode;
	// 起始顶点到当前顶点的总路径长度
	public int totalWeight;

	public Path(int preNode, int totalWeight)
	{
		this.preNode = preNode;
		this.totalWeight = totalWeight;
	}
}

/// <summary>  
/// Dijkstra算法  
/// </summary>  
/// <param name="graph"></param>  
/// <param name="startIndex"></param>
public Path[] Dijkstra<T>(GraphByAdjacencyMatrix<T> graph,int startIndex)
{
	// 用来存储顶点是否访问过
	bool[] flags = new bool[graph.Count];
	// 存储起始顶点到其他各顶点的最短路径长度
	Path[] paths = new Path[graph.Count];

	// 初始化起始顶点到其他顶点的路径
	for (int i = 0; i < graph.Count; i++)
	{
		paths[i] = new Path(startIndex, graph.Matrix[startIndex, i]);
	}
	// 将初始顶点设为已访问
	flags[startIndex] = true;
	int minIndex = 0;
	
	for (int i = 1; i < graph.Count; i++)
	{
		int min = Int32.MaxValue;
		// 寻找已存储路径中的最短路径
		for (int j = 0; j < graph.Count; j++)
		{
			if (!flags[j] && paths[j].totalWeight < min)
			{
				min = paths[j].totalWeight;
				minIndex = j;
			}
		}
		
		// 将最近的顶点设为已访问
		flags[minIndex] = true;
		// 基于当前顶点,查找更远顶点的最短路径
		for (int j = 0; j < graph.Count; j++)
		{
			// 把min放在右侧防止溢出
			if (!flags[j] && graph.Matrix[minIndex, j] < paths[j].totalWeight - min)
			{
				paths[j].preNode = minIndex;
				paths[j].totalWeight = min + graph.Matrix[minIndex, j];
			}
		}
	}

	return paths;
}

/// <summary>
/// 输出最短路径
/// </summary>
/// <param name="graph"></param>
/// <param name="startIndex"></param>
/// <param name="endIndex"></param>
private void PrintShortestPathByDijkstra<T>(GraphByAdjacencyMatrix<T> graph,int startIndex,int endIndex)
{
	var paths = Dijkstra<T>(graph, startIndex);
	var stack = new Stack<T>(graph.Count);
	int curIndex = endIndex;
	
	while (curIndex != startIndex)
	{
		stack.Push(graph.Nodes[curIndex]);
		curIndex = paths[curIndex].preNode;
	}
	stack.Push(graph.Nodes[startIndex]);
	while (stack.Count > 0)
	{
		Console.Write(stack.Pop());
		if(stack.Count != 0)
			Console.Write("->");
	}
	
	Console.Write(" 路径长度="+paths[endIndex].totalWeight);
}

代码部分也与Prim算法的代码高度相似。引用一位知乎大佬的话来说，Prim算法更新的是未标记集合到已标记集合之间的距离；而Dijkstra算法更新的是原点到未标记集合之间的距离。

二、Floyd算法

与Dijkstra算法相比，Floyd算法就显得比较“暴力”了。我们来看下面这张图

假设我们要求从A到B的最短路径。首先最直观的路径就是A直接到B：A->B = 9。但假如我们找一个中间节点，也就是C，就会发现A->C->B = 7要比A->B = 9更短。因此现在A到B的最短路径更新为：A->C->B = 7。

接下来看C点。C到B的直连路径为：C->B = 3。但是如果找中间节点D，就会发现C->D->B = 2比C->B = 3更短。因此C到B的最短路径更新为：C->D->B = 2。

最终，A到B的最短路径就是：A->C->D->B = 6。

这就是Floyd算法的核心思想。

下面来通过一个具体的例子讲解算法流程。首先需要准备两个二维数组，weights数组用来存储各顶点之间的路径长度，paths数组用来存储路径的中间节点。在初始状态下，weights数组初始化为与图的邻接矩阵一致，paths数组初始化为路径的尾结点（如A->B的中间节点设置为B）。

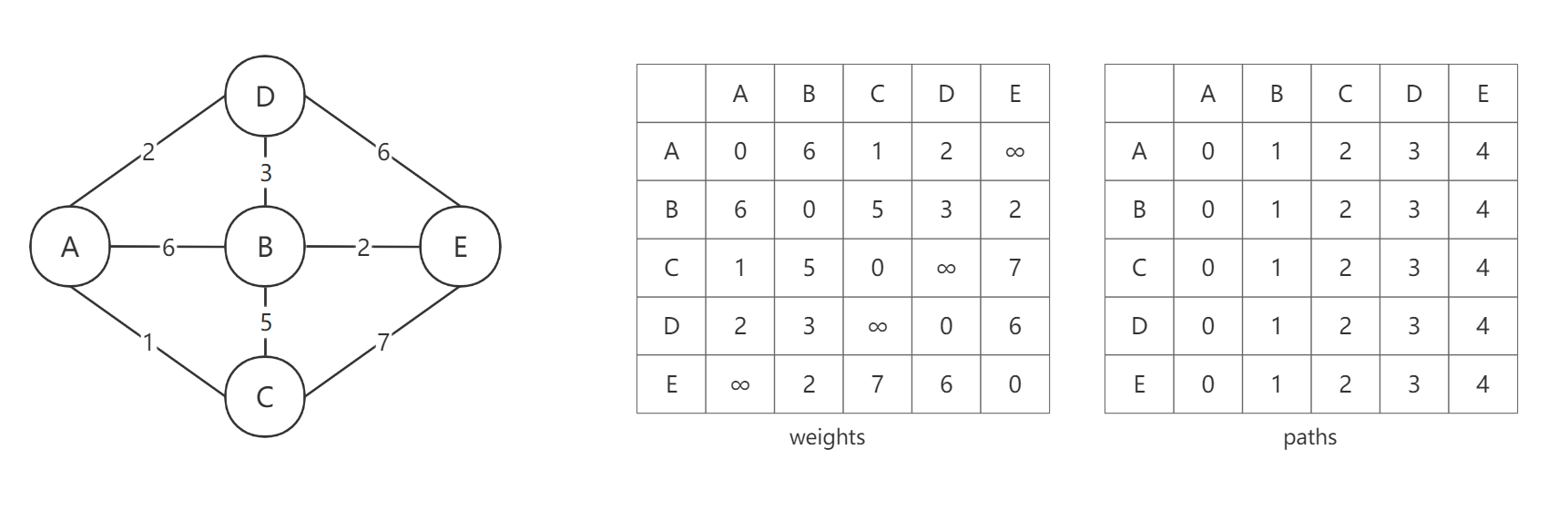
首先，以A节点为中间节点，计算其他两个顶点经过A点相连的路径和，并与直连的路径相比较。如果经过A节点的方案更短，则更新到这两个矩阵中。比如B->C = 5，如果经过A节点则B->A->C = 7，路径变长了，所以不需要更新。又如C->D = ∞，如果经过A节点，则C->A->D = 3，路径变短了，所以需要更新。

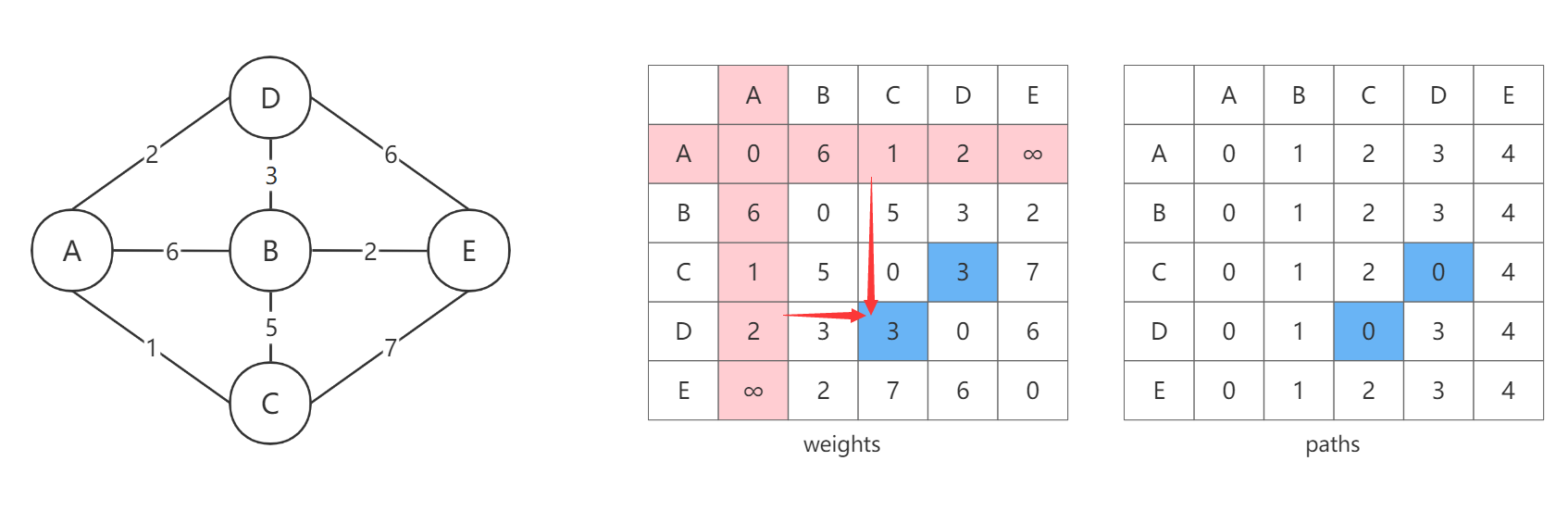
接下来再以B为中间节点进行计算。

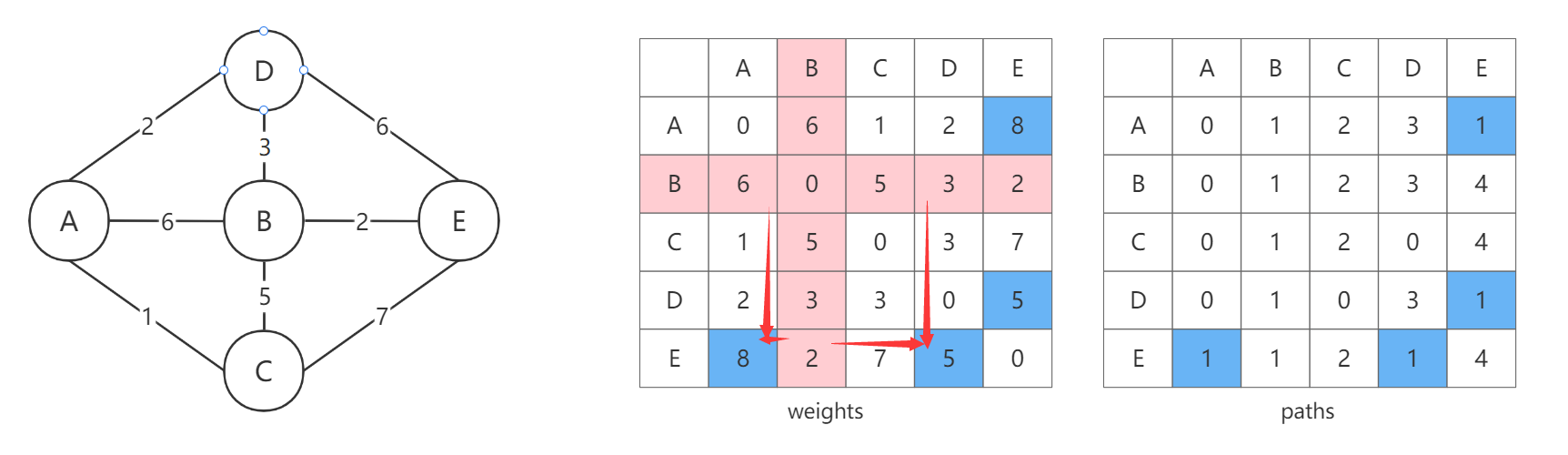
以此类推，直到整个矩阵全部更新完。最终的结果如下

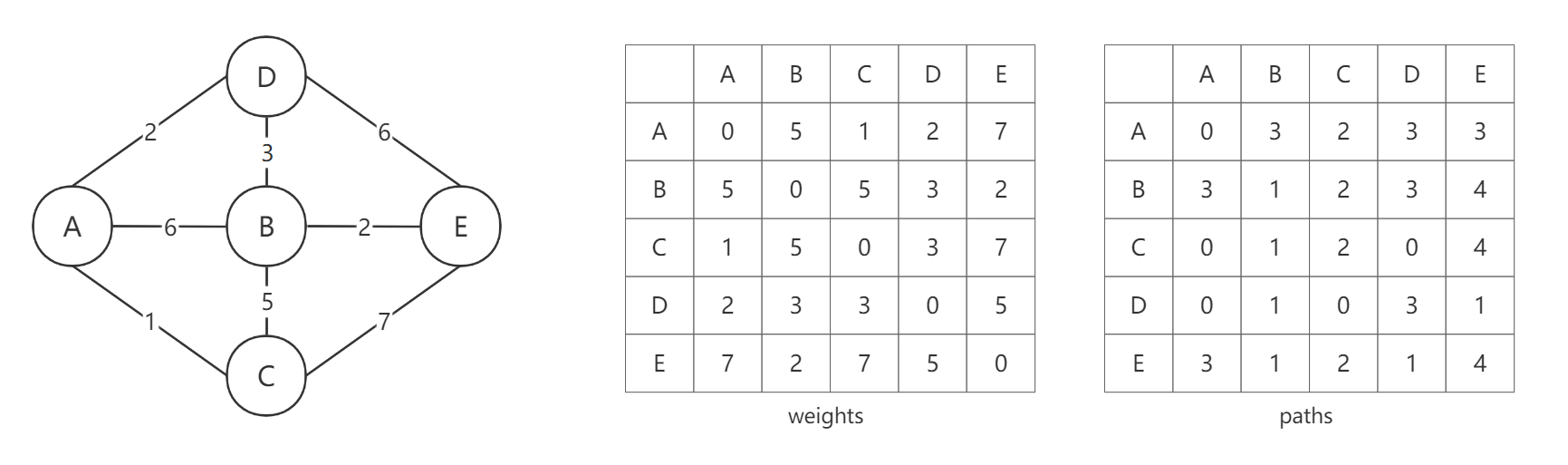
现在假如我们要找A到E的最短路径。从weights数组可得A到E的最短路径长度为7。然后根据paths求得具体路径。首先根据paths[0][4] = 3可知，从A到E需要经过D点，也就是A->D。然后再根据paths[3][4] = 1可知，从D到E需要先经过B点，即A->D->B。再根据paths[1][4] = 4可知，从B到E可以直达，即A->D->B->E。

代码如下

/// <summary>
/// Floyd算法
/// </summary>
/// <param name="graph"></param>
public Path[,] Floyd<T>(GraphByAdjacencyMatrix<T> graph)
{
	// 这里可以复用前面的Path结构体
	Path[,] paths = new Path[graph.Count,graph.Count];
	
	// 将路径长度初始化为与邻接矩阵一致
	// 将路径中间点初始化为边的尾结点
	for (int i = 0; i < graph.Count; i++)
	{
		for (int j = 0; j < graph.Count; j++)
		{
			paths[i, j].totalWeight = graph.Matrix[i, j];
			paths[i, j].preNode = j;
		}
	}

	// 依次寻找经过中间节点小于直达的路径
	for (int nodeIndex = 0; nodeIndex < graph.Count; nodeIndex++)
	{
		for (int row = 0; row < graph.Count; row++)
		{
			for (int col = 0; col < graph.Count; col++)
			{
				// 求和转换为求差防止溢出
				if (paths[row, col].totalWeight - paths[nodeIndex,col].totalWeight > paths[row,nodeIndex].totalWeight )
				{
					paths[row, col].totalWeight =
						paths[row, nodeIndex].totalWeight + paths[nodeIndex, col].totalWeight;
					paths[row, col].preNode = nodeIndex;
				}
			}
		}
	}
	return paths;
}

/// <summary>
/// 输出最短路径
/// </summary>
/// <param name="graph"></param>
/// <param name="startIndex"></param>
/// <param name="endIndex"></param>
private void PrintShortestPathByFloyd<T>(GraphByAdjacencyMatrix<T> graph,int startIndex,int endIndex)
{
	var paths = Floyd<T>(graph);
	int curIndex = startIndex;
	
	while (curIndex != endIndex)
	{
		Console.Write(graph.Nodes[curIndex]+"->");
		curIndex = paths[curIndex, endIndex].preNode;
	}
	Console.Write(graph.Nodes[endIndex]);
	Console.Write(" 路径长度="+paths[startIndex,endIndex].totalWeight);
}