C++算法：排序

排序之一（插入、冒泡、快速排序）
排序之二（归并、希尔、选择排序）
排序之三（堆排序）
排序之四（计数、基数、桶排序）

---

---

本文续：C++算法：排序之二（归并、希尔、选择排序）

---

二、比较排序算法

7、堆排序

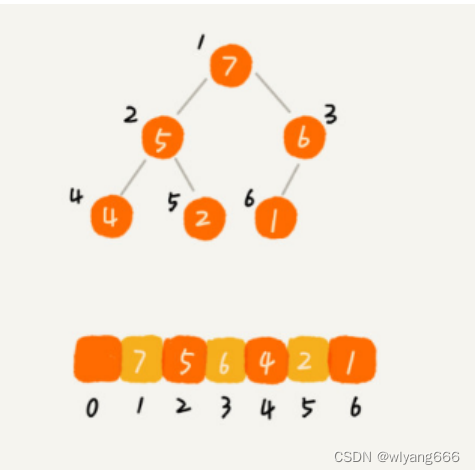
堆排序和前面C++数据结构：二叉树之一（数组存储）提到的特抽象的二叉树很有关系，文中提到的完全二叉树的数组存储法，就是堆排序的关键。一般我们都采用大顶堆（也叫大根堆，根节点最大的意思）的方式进行排序，实现的核心思想就一句话：就是一直保持任一根节点总是大于左右子节点的。

很明显这是一个牵一发而动全身的工作，调整了一个结点使其符合大顶堆规则了，可能别的节点又不符合了，我们先找一个静态图片来说明这个问题再看动态图就好理解了：

• 1、假设存在以下一个符合大顶堆的特征的二叉树，至于一个数组它为什么是二叉树，不明白的去看前文。
  

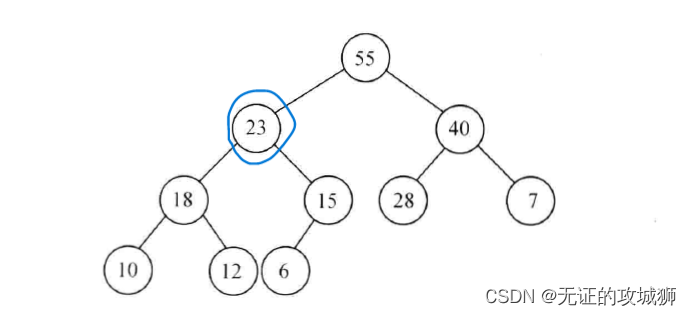
• 2、然后我们将图中标记的23替换成5，用以说明调整过程：
  

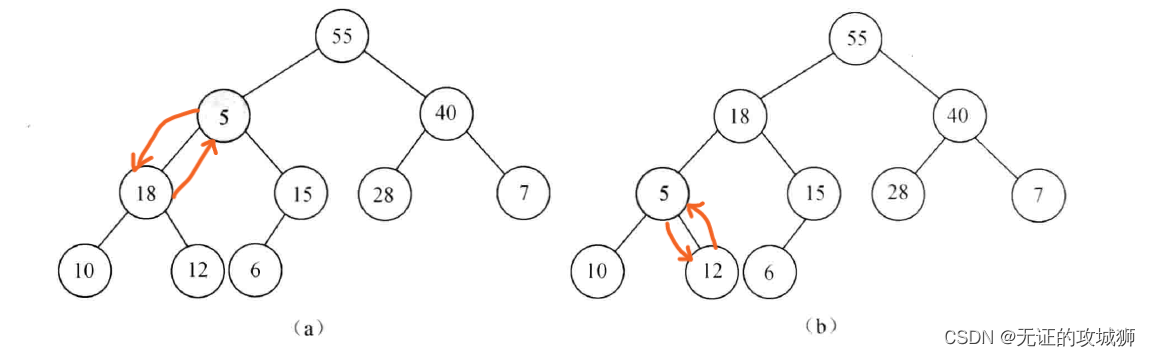
• 3、替换成5后，作为根节点，见图a：它比左节点18、右节点15都要小，所以和它的子节点中的最大的交换，就是和左节点18交换，之后就成了图b所示的样子。显然5还是一个根节点，它又比左右节点都要小，所以要继续和子节点中最大的12交换。
  

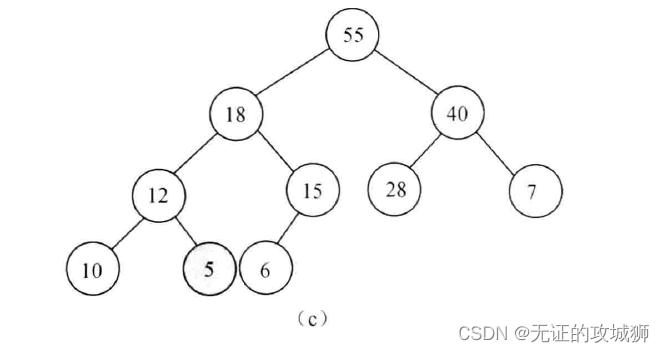
• 4、图c就是最后完成的样子，节点5最终被移到了右叶子节点，整个二叉树又符合大顶堆的特性了。理解了这个逻辑再看下面的动图就很容易明白了。

动图中后期标红的就是排序过程，在初次完成大顶堆的调整后，将根节点移动到层序遍历的最后一个节点，根据数组存储的规律其实就是数组的最后一个元素。如此就造成了大顶堆特性不满足了，那就把最后一个元素从循环中剔除再交换其余元素，使其满足大顶堆特性，如此循环直到完成排序。

代码如下（示例）：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

void keep_heap(vector<int> &vec, int len, int node){ 
/*调整结点符合大顶堆特性，len是数组长度，排序时会递减这个值用以排除数组后面已排序的元素，
所以要传递这个参数, node是非叶子节点下标*/

    int left, right, biggest;
    biggest = node;         //某分支的三个节点中最大的，先默认为根；
    left = node * 2 + 1;    //左节点的下标，因为从0开始，所以要加1
    right = node * 2 + 2;   //右节点的下标，因为从0开始，所以要加2
    if (left<len && vec[left] > vec[biggest]){  //要保证不调整已排序的节点
        biggest = left;
    }
    if (right<len && vec[right] > vec[biggest]){
        biggest = right;
    }
    if (biggest != node){       //调整为根节点最大
        swap(vec[node], vec[biggest]);
        keep_heap(vec, len, biggest);  //递归调整交换后的节点，biggest是下标，不会被交换
    }

}

void big_heap(vector<int> &vec){   //第一次建立大顶堆要遍历所有非叶子节点
    int len = vec.size();
    int node = len/2 - 1;  //根据完全二叉树的规则，非叶子节点数是：节点数/2 -1
    while (node >= 0){
        keep_heap(vec, len, node);
        node--;
    }
}

void heap_sort(vector<int> &vec){  //排序函数
    int len = vec.size();
    big_heap(vec);               //第一次建立大顶堆
    for (int i=len-1; i>0; i--){    //开始将最大元素（根节点）交换到数组后面
        swap(vec[0], vec[len-1]);   //将大顶堆的根交换到数组最后面
        len--;                      //排除已交换的下标
        keep_heap(vec, len, 0);     //重建大顶堆
    }
}

int main(){
    vector<int> vec = {91,60,96,13,35,65,46,65,10,30,20,31,77,81,22};
    heap_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

堆排序是一种很优秀的排序算法，具备了插入排序和归并排序的一些特征。时间复杂度是O(NlogN)，又是就地排序，所以应用范围很广。这种排序法是在完全二叉树这种数据结构上实现的，那么显然它也可以用于链表结构，只是实现起来要麻烦得多，因为不能用下标操作。但是改进一下代码也是可以实现的，比如笔者曾经花了点时间写了个可以用下标操作的List。当然这是个笨办法，还可以用迭代器来实现。

C++的标准模板库中的 sort 排序就用到了堆排序，再比如游戏服务器排行榜那这种方式排序就太合适了。

在开发游戏排行榜功能时，由于游戏中的玩家不停地进入服务器，离开服务器，所以我们的元素个数是动态的，使用其他的一些算法只能应对一些一次性把所有的元素算完的情况。而如果使用堆排序，就可以不断地往堆里增加元素而不需要重新排序，这就是堆排序的优势。

比如你要在10万个人里排出前100名，这时不管10万个人怎样进进出出，只要进入一个就push一个，只要保证堆里有100个人就可以了，而且这个排行榜的开销也是很低的，只是在这100个元素里进行最小顶堆排序。这样就可以快速地更新游戏服务器在线排名

所以本系列排序算法文章单独给堆排序写了一文，一方面是这个排序法用到了完全二叉树这种数据结构，解释清楚比较费字还费图。另一方面，这种排序和快速排序一样重要，只要你想当个正经码农，就必须熟练掌握的。至于小顶堆的实现，也就不用单独再费神来实现一遍了，把比较大小部分的大于号改成小于号就行了，当然你最好改个变量名是吧？

好了，十大排序法中所有比较排序的算法都写完了，下一节就是非比较排序了。

---

未完待续…