前言
之前介绍的都是二叉查找树,二叉树一个节点最多有两个子节点,那么多于两个节点是什么情况呢,这就是我们本节要介绍的多路查找树。
多路查找树,也是我们数据库mysql底层索引维护方式。下面,我们来详细介绍。
1. B 树
1.1 定义
1.1.1 多路查找树
多路查找树(muitl-way search tree),其每一个节点的孩子数可以多于两个,且每一个节点处可以存储多个元素。
1.1.2 B 树
B树(BalanceTree)是对二叉查找树的改进。它的设计思想是,将相关数据尽量集中在一起,以便一次读取多个数据,减少硬盘操作次数。
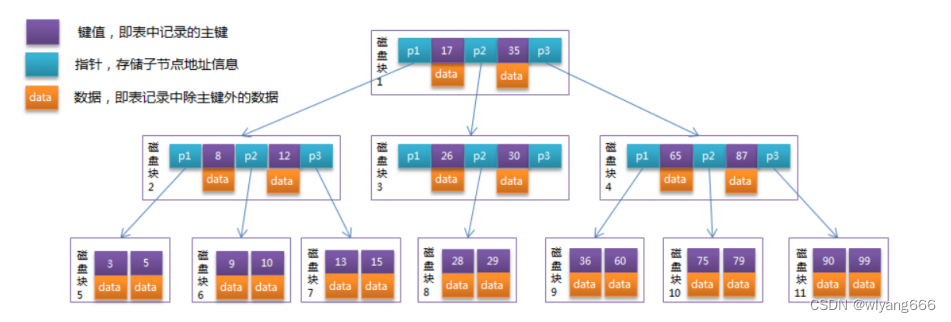
1.2 特征
一棵m阶的B 树 (m叉树)的特性如下:
- B树中所有节点的孩子节点数中的最大值称为B树的阶,记为M
- 树中的每个节点至多有M棵子树 —即:如果定了M,则这个B树中任何节点的子节点数量都不能超过M
- 若根节点不是终端节点,则至少有两棵子树
- 除根节点和叶节点外,所有点至少有m/2棵子树
- 所有的叶子结点都位于同一层
2. B+ 树
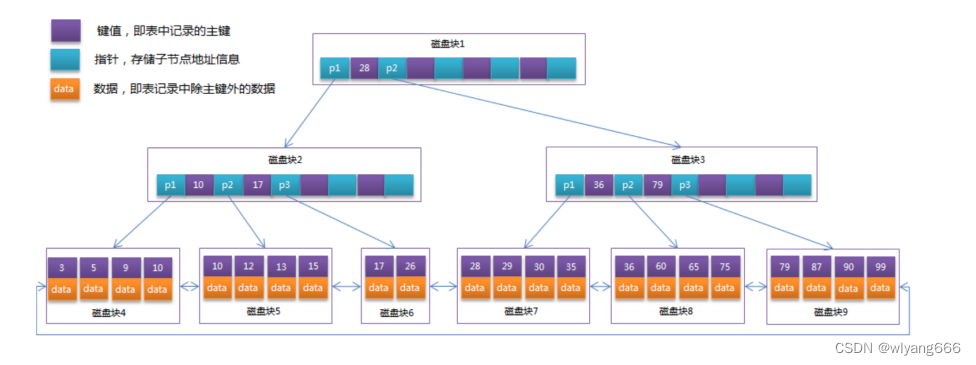
2.1 特征
B+树是B-树的变体,也是一种多路搜索树,其定义基本与B树相同,它的自身特征是:
- 非叶子结点的子树指针与关键字个数相同
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
- 为所有叶子结点增加一个链指针
- 所有关键字都在叶子结点出现
2.2 B和B+的区别
- B树和B+树的最大区别在于非叶子节点是否存储数据的问题。
- B树是非叶子节点和叶子节点都会存储数据。
- B+树只有叶子节点才会存储数据,而且存储的数据都是在一行上,而且这些数据都是有指针指向的,也就是有顺序的。
2.3 应用
2.3.1 MySQL索引B+Tree
- B树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树。
- B树的高度一般都是在2-4这个高度,树的高度直接影响IO读写的次数。
- 如果是三层树结构,支撑的数据可以达到20G;如果是四层树结构,支撑的数据可以达到几十T
3. 二叉堆
二叉堆本质上是一种完全二叉树,它分为两个类型
3.1 定义
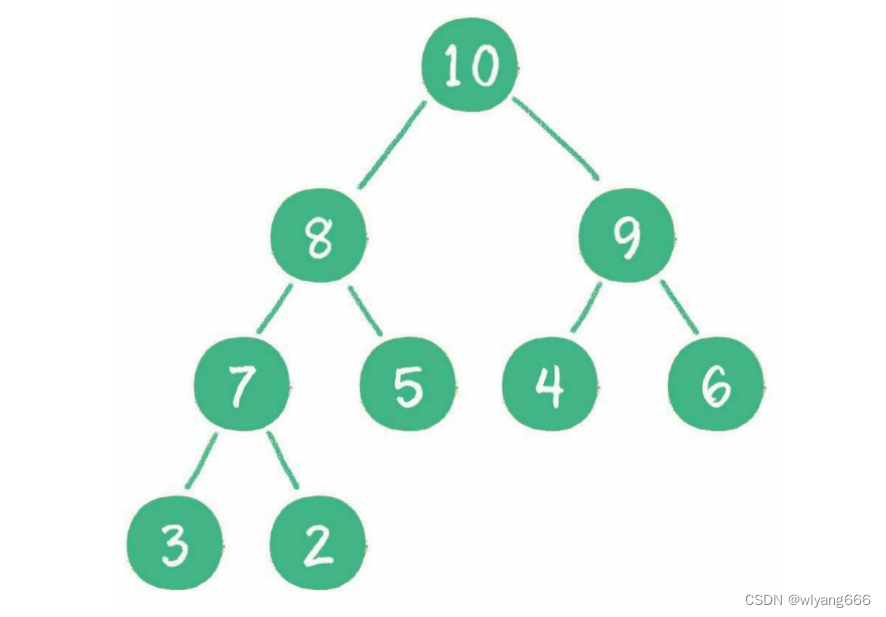
3.1.1 大顶堆(最大堆)
最大堆的任何一个父节点的值,都大于或等于它左、右孩子节点的值。
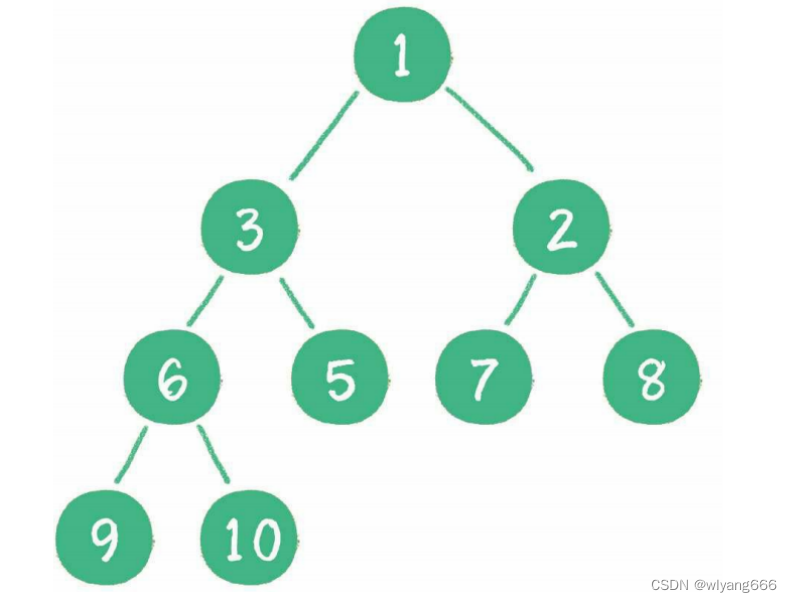
3.1.2 小顶堆(最小堆)
最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
3.2 存储原理
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
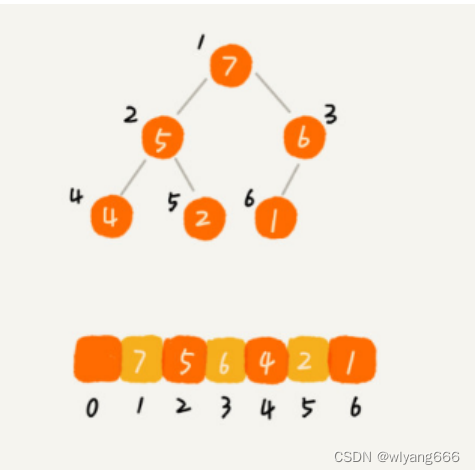
如上图所示,数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 i/2 取整的节点。
3.3 二叉堆的典型应用
- 优先队列
- 利用堆求 Top K问题
在一个包含 n 个数据的数组中,我们可以维护一个大小为 K 的小顶堆,顺序遍历数组,从数组中取出数据与堆顶元素比较。如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;如果比堆顶元素小,则不做处理,继续遍历数组。这样等数组中的数据都遍历完之后,堆中的数据就是前 K 大数据了