深度学习目录

1. 自适应线性单元 (Widrow and Hoff, 1960)
2. 神经认知机 (Fukushima, 1980)
3. GPU-加速 卷积网络 (Chellapilla et al., 2006)
4. 深度玻尔兹曼机 (Salakhutdinov and Hinton, 2009a)
5. 无监督卷积网络 (Jarrett et al., 2009b)
6. GPU-加速 多层感知机 (Ciresan et al., 2010)
7. 分布式自编码器 (Le et al., 2012)
8. Multi-GPU 卷积网络 (Krizhevsky et al., 2012a)
9. COTS HPC 无监督卷积网络 (Coates et al., 2013)
10. GoogLeNet (Szegedy et al., 2014a)

自编码器（autoencoder）

当前（2018）主流技术是卷积网络和自编码器

自编码器是一种有效的数据维度压缩算法，主要应用在如下两个方面：

• 构建一种能够 重构输入样本 并 进行特征表达 的 神经网络：对输入样本进行降噪或去除冗余信息。
• 训练多层神经网络时，通过自编码器训练样本，得到参数初始值：在多层神经网络种得到最优参数

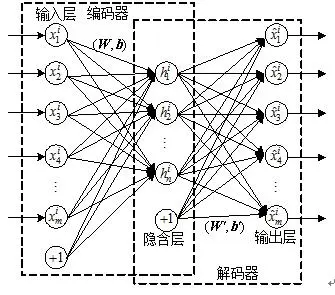
自编码器是一种能够重构输入样本的三层神经网络。
我们把输入层到中间层之间的映射称为编码。
把中间层到输出层之间的映射称为解码。

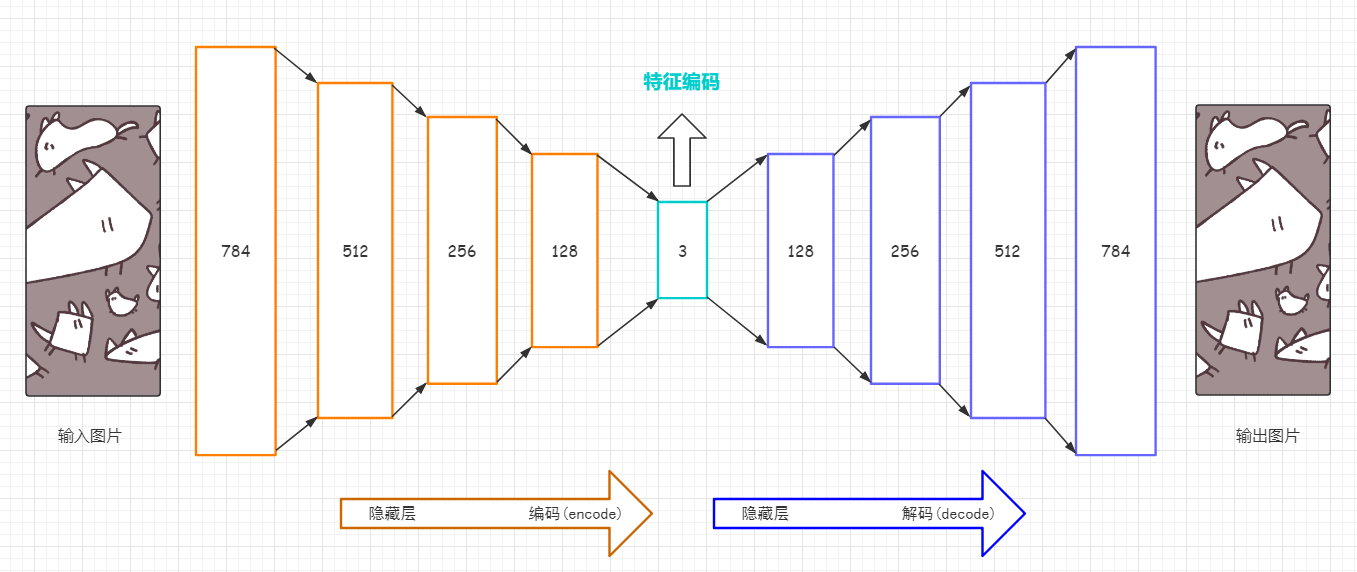
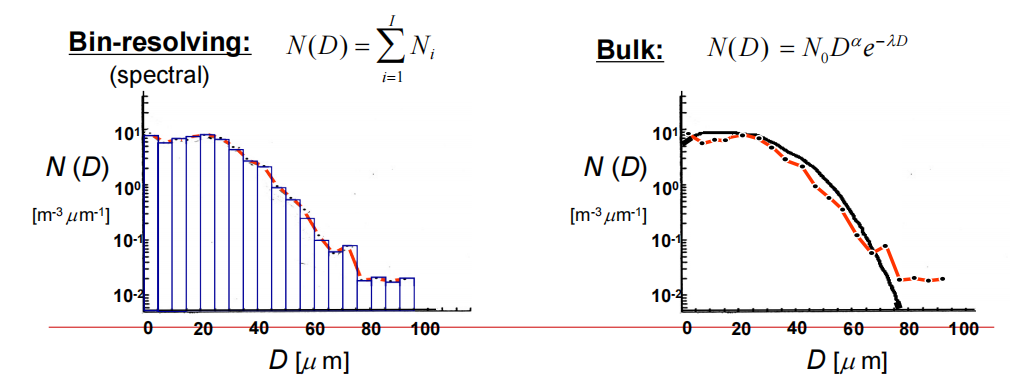
自编码器可以将高维信息进行压缩后再重构

自编码器的训练

编码公式：
$$y=f(Wx+b)，f表示编码器激活函数$$
解码公式
$$\tilde{x}=\tilde{f}(\tilde{W}y+\tilde{b})，\tilde{f}表示解码器激活函数$$

自编码器与受限玻尔兹曼机的区别

• 自编码器和受限玻尔兹曼机的结构都是两层
• 受限玻尔兹曼机是一个概率模型，训练的目的是求出能够使似然函数达到极大值的参数估计。
• 自编码器需要定义一个误差函数，通过调整参数使得输入样本和重构结构的误差收敛到极小值。
• 自编码器的计算结果也会进行正向传播

降噪自编码器

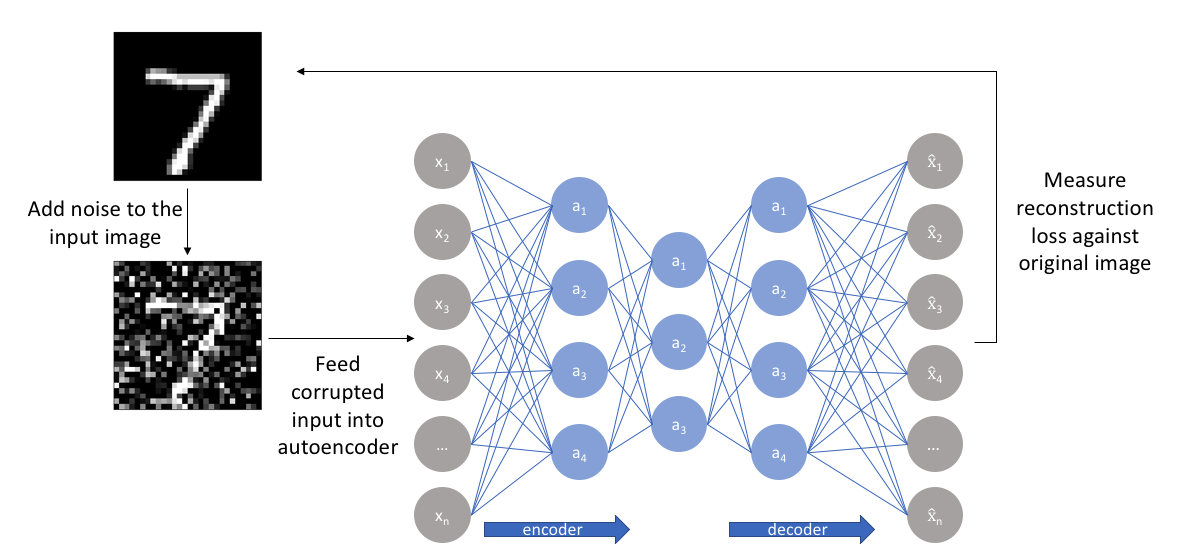
1. 首先对训练样本添加随机噪声得到含有噪声的样本
2. 对样本进行编码和解码
3. 将解码结构与原图（不含噪声的样本）进行误差分析
4. 将误差反向传播，修改网络权重

稀疏自编码器

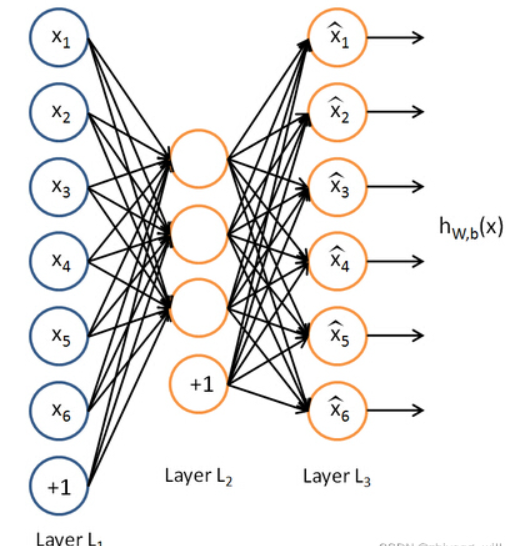
将稀疏正则化引入到自编码器。通过增加正则化项，大部分单元的输出都变为0，这样就能利用少数单元有效完成压缩或重构。

稀疏自动编码

栈式自编码器（stacked autocoder）

把输入层和中间层多层堆叠后，就可以得到栈式自编码器。

栈式自编码器和深度信念网络一样，都是逐层训练，从第二层开始，前一个自编码器的输出作为后一个自编码器的输入。
经过多次堆叠，栈式自编码器能够有效完成输入模式的压缩。

在预训练中的应用

栈式自编码器和多层神经网络都能得到有效的参数，所有我们可以把训练后的参数作为神经网络或卷积神经网络的参数初始值，这种方法叫做预训练。