I. 尺度悖论的概述
尺度悖论是指在某些系统或现象中,尺度的大小或范围会对其性质、行为或理解产生矛盾或困难的现象。尺度悖论常出现在自然科学、社会科学和哲学等领域中,引发了一系列有关尺度和尺度变化对系统行为的影响的研究。

II. 举3个简单的例子
例子1
考虑一片森林,如果我们在不同的尺度上观察它,我们会得到不同的结论。如果我们只观察森林的整体,我们可能会认为这是一个稳定的系统,但如果我们仔细观察每一个树木和植物,我们会发现它们之间的关系非常复杂。在这种情况下,我们可能会得出不同的结论和预测。
例子2
我们比较城市A和城市B的平均房价。假设城市A的平均房价为100万元,城市B的平均房价为50万元。如果我们只看这个数据,就可能得出结论说城市A的房价比城市B高,但这个结论可能是错误的。因为城市A和城市B的规模不同,城市A可能比城市B有更多的高端住宅区,而城市B可能有更多的中低端住宅区。这就意味着我们需要考虑到城市规模的尺度效应。
例子3
人口普查时,需要用抽样检查去推测总体的人口时,不同的样本框代表不同的总体(代表性有强弱)。2021年普查了广州天河1%的群体有10w人,普查了广州海珠区10%的群体共5w人。若23年的普查为天河1%的群体有9w人,普查了广州海珠区10%的群体共70w人。
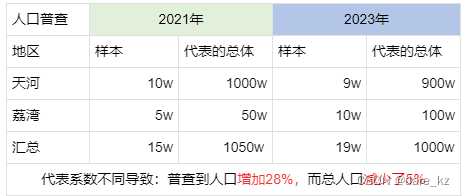
代表系数(观察尺度)不一样,导致观察到的情况和推测的情况不一样
忽略或捕捉到不同的因素和变量,从而导致结论的差异。
III. 尺度悖论与辛普森悖论的区别
尺度悖论和辛普森悖论都是由于对数据的分组或处理方式不同而导致的悖论。它们都是一种统计上的现象,可以引起混淆和误解。在处理数据时,必须认识到这些悖论的存在,并采取适当的措施避免误导性的结论。
辛普森悖论与尺度悖论的相似之处
尺度悖论和辛普森悖论之间的相似之处在于,它们都是由于忽略或混淆数据的不同层次而导致的。在尺度悖论中,数据的尺度或比例被忽略,从而导致错误的结论。在辛普森悖论中,数据的不同组合或分组被忽略,从而导致错误的结论。
尺度悖论与辛普森悖论的不同之处
不同之处在于,尺度悖论强调数据的比例和尺度问题,而辛普森悖论强调数据的分组和组合问题。此外,尺度悖论通常涉及到数量级的问题,而辛普森悖论通常涉及到不同的样本组合。
适用范围不同:尺度悖论通常适用于连续型变量,如时间序列、空间数据等;而辛普森悖论适用于分类变量或分组数据。
影响因素不同:尺度悖论的影响因素主要来自于数据本身的特性,例如观察的尺度或数据的空间分布;而辛普森悖论的影响因素主要来自于子组的组成,即不同的子组组合方式可能导致不同的总体趋势或规律。
分析方法不同:解决尺度悖论通常需要通过控制变量、合理选择尺度或采用多尺度分析等方法来避免;而解决辛普森悖论通常需要更细致地分析子组之间的关系,或者通过逐步分解子组并逐一分析等方法来解决。
IV. 尺度悖论在各领域的普遍存在
物理学中的尺度悖论 在物理学中,尺度悖论指出,在一些物理现象中,当尺度缩小到微观层面或极小范围时,经典物理理论无法准确描述系统的行为,需要引入量子力学的概念。例如,电子在经典物理学中被视为粒子,但在微观尺度下,它表现出波动性质,只能用量子力学来解释。
社会科学中的尺度悖论 在社会科学中,尺度悖论涉及到个体和集体之间的关系。在某些情况下,个体的行为和决策可能与集体的行为和决策产生矛盾。例如,个体可能追求自身利益最大化,但这种追求可能导致整个社会或群体的利益受损。
哲学中的尺度悖论 在哲学中,尺度悖论涉及到对现实的认识和理解。有时,我们通过不同的尺度或视角来观察和解释现实,会得出不同或甚至相互矛盾的结论。这引发了一些哲学上的问题,例如主体与客体的关系、相对性理论等。

V. 解决尺度悖论的方法
1.尽可能使用同样尺度的数据:在进行统计分析时,要尽可能使用相同尺度的数据,以避免数据的不一致性导致的错误结论。例如,在比较两个城市的人均收入时,应使用同一货币单位,而不是将它们转换成不同的货币单位进行比较。
2.考虑到尺度效应:尺度效应是指不同尺度下观察到的现象差异,例如城市尺度和个体尺度下的收入差异。在进行统计分析时,要考虑到这种效应,并进行相应的调整。
3.对样本进行更详细的描述:在进行统计分析时,要对样本的特征进行详细的描述,例如样本的大小、分布、组成等,以避免因样本特征不清晰而导致的错误结论。
4.进行多层次分析:多层次分析是指将数据按照层次结构进行分析,例如将城市、行政区、社区和个体作为不同的层次进行分析。这种方法可以更好地考虑到不同尺度下的差异和交互作用,从而避免尺度悖论的出现。

VI. 结论
尺度悖论在科学研究和数据分析中具有重要的影响。它提醒我们在进行数据分析和推断时要考虑观察尺度的影响,并意识到不同尺度下的数据关系可能是复杂和多样的。因此,我们需要谨慎地选择和解释数据,以避免由尺度悖论引起的错误推断和结论。