算法的定义和特征
什么是算法?
算法是求解某一特定问题的一组有穷规则的集合,它是由若干条指令组成的有穷符号串。
算法的五个重要特性:
- 确定性:每一条指令都必须有确切的含义。不存在二义性,只有一个入口和出口。
- 可实现性:算法可以通过已经实现的基本运行指令有限次来实现。
- 输入:有另个或多个输入,取自于某个特定对象的集合。
- 输出:有一个或多个输出,输出与输入有某些特定关系。
- 有穷性:一个算法必须在执行有穷步后结束,且每一步都在有穷时间内完成。
算法设计的质量指标:
- 正确性
- 可读性
- 健壮性
- 效率与存储量
算法和程序的区别
程序:对一个算法使用某种程序设计语言的具体实现。
算法的有穷性意味着不是所有的计算机程序都是算法。
算法复杂性
=算法所需要的计算机资源=时间复杂性+空间复杂性
一般情况下只考虑三种情况的时间复杂性:最坏情况、最好情况和平均情况。
算法分类(计算时间)
多项式时间算法:可用多项式对其计算时间限界的算法。
O(1) < O(log n) < O(n) < O(nlog n) < O(n2)
指数时间算法:计算时间用指数函数限界的算法。
O(2n) < O(n!) < O(nn)
当n取值较大时,指数时间算法和多项式时间算法在计算时间上非常悬殊。
最优算法
问题的计算时间下界为Ω(f(n)),则计算时间复杂性为O(f(n))的算法是最优算法。
例如,排序问题的计算时间下界为Ω(nlogn),计算时间复杂性为O(nlogn)的排序算法是最优算法。
递归的分类
- 基于归纳法的递归
- 基于分治法的递归
Fibonacci数列
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。它可以递归地定义为:

int fibonacci(int n){
if(n <= 1){
return 1;
}
return fibonacci(n-1)+fibonacci(n-2);
}
递归优缺点
- 优点:结构清晰,可读性强,且容易用数学归纳法证明算法的正确性,因此它为设计算法、调试程序带来很大方便。
- 缺点:递归算法的运行效率低,无论是耗费的计算时间还是占用的存储空间都比非递归算法多。
分治法思想
将一个难以解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治法的适用条件
- 该问题的规模缩小到一定的程序就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
分治法的复杂性分析
分治法将规模为n的问题分成k个规模为n/k的子问题去解。设分解阈值为1,解规模为1的问题耗费1个单位时间。再设分解与合并的时间需要f(n)个单位时间,则:
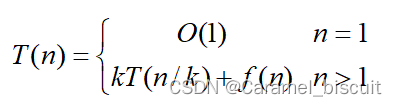
Master定理(递归复杂度判定定理)

二分搜索技术
已按升序排好序的n个元素a[0:n-1],现要在这n个元素中找出一特定元素x。
int binarySearch(int a[],int x,int l,int r){
while(l <= r){
int index = (l+r)/2;
if(a[index] == x){
return index;
}else if(a[index] < x){
l = index + 1;
}else{
r = index - 1;
}
}
return -1;
}
算法复杂度分析:每执行一次算法的while循环,待搜索数组的大小减少一半。因此,在最坏情况下,while循环被执行了O(log n)次,循环体内运算需要O(1)时间,因此整个算法在最坏情况下的计算时间复杂性为O(log n)。
合并排序
将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
void mergeSort(int a[],int left,int right){
//至少有2个元素才能进行合并
if(left < right){
int mid = (left + right)/2;
mergeSort(a,left,mid);
mergeSort(a,mid+1,right);
merge(a,b,left,mid,right); //合并到数组B
copy(a,b,left,right); //复制回数组A
}
}