基于连续小波变换的厄尔尼诺海平面周期变化数据集分析
- 1. 厄尔尼诺海平面周期变化数据集介绍
- 2. 基于连续小波变换的信号分析
- 2.1 原始信号读取可视化
- 2.2 傅里叶变换结果可视化
- 2.3 小波变换结果可视化
- 参考资料
- 后记
1. 厄尔尼诺海平面周期变化数据集介绍
这些数据是通过国际热带海洋全球大气(TOGA)计划开发的热带大气海洋(TAO)阵列收集的。TAO阵列由横跨赤道太平洋的近70个系泊浮标组成,用于测量海洋学和地面气象变量,这些变量对于改进热带地区的季节性到年际气候变化的探测、理解和预测至关重要,最明显的是与厄尔尼诺/南方涛动(ENSO)周期有关的变化。
系泊系统由国家海洋和大气管理局(NOAA)太平洋海洋环境实验室(PMEL)开发。每个系泊装置测量500米深处的空气温度、相对湿度、表面风、海面温度和地下温度,少数浮标测量海流、降雨量和太阳辐射。阵列中的数据和当前更新可以在此地址的web上查看。
1982-1983年的厄尔尼诺/南方涛动(ENSO)周期是本世纪最强的一次,在全世界造成了许多问题。秘鲁和美国等世界部分地区因降雨量增加而遭受破坏性洪水,而西太平洋地区则遭遇干旱和毁灭性森林火灾。ENSO周期在接近峰值之前既没有被预测,也没有被探测到。这突出了海洋观测系统(即TAO阵列)的必要性,以支持季节到年际时间尺度上大规模海洋-大气相互作用的研究。
TAO阵列为世界各地的气候研究人员、天气预报中心和科学家提供实时数据。使用ENSO周期数据可以提前一到两年预测热带太平洋温度。这些预测是可能的,因为系泊浮标、漂流浮标、自愿船舶温度探测器和海平面测量。
此处用到的厄尔尼诺数据集是一个用于跟踪厄尔尼诺的时间序列数据集,包含1871年至1997年的每季度海面温度测量值。
2. 基于连续小波变换的信号分析
2.1 原始信号读取可视化
import matplotlib.pyplot as plt
import pywt
import numpy as np
import pandas as pd
from scipy import fftpack
def get_ave_values(xvalues, yvalues, n = 5):
signal_length = len(xvalues)
if signal_length % n == 0:
padding_length = 0
else:
padding_length = n - signal_length//n % n
xarr = np.array(xvalues)
yarr = np.array(yvalues)
xarr.resize(signal_length//n, n)
yarr.resize(signal_length//n, n)
xarr_reshaped = xarr.reshape((-1,n))
yarr_reshaped = yarr.reshape((-1,n))
x_ave = xarr_reshaped[:,0]
y_ave = np.nanmean(yarr_reshaped, axis=1)
return x_ave, y_ave
def plot_signal_plus_average(time, signal, average_over=5):
fig, ax = plt.subplots(figsize=(15, 3))
time_ave, signal_ave = get_ave_values(time, signal, average_over)
ax.plot(time, signal, label='signal')
ax.plot(time_ave, signal_ave, label='time average (n={})'.format(5))
ax.set_xlim([time[0], time[-1]])
ax.set_ylabel('Signal Amplitude', fontsize=18)
ax.set_title('Signal + Time Average', fontsize=18)
ax.set_xlabel('Time', fontsize=18)
ax.legend()
plt.show()
dataset = "http://paos.colorado.edu/research/wavelets/wave_idl/sst_nino3.dat"
df_nino = pd.read_table(dataset)
N = df_nino.shape[0]
t0 = 1871
dt = 0.25
time = np.arange(0, N) * dt + t0
signal = df_nino.values.squeeze()
plot_signal_plus_average(time, signal)
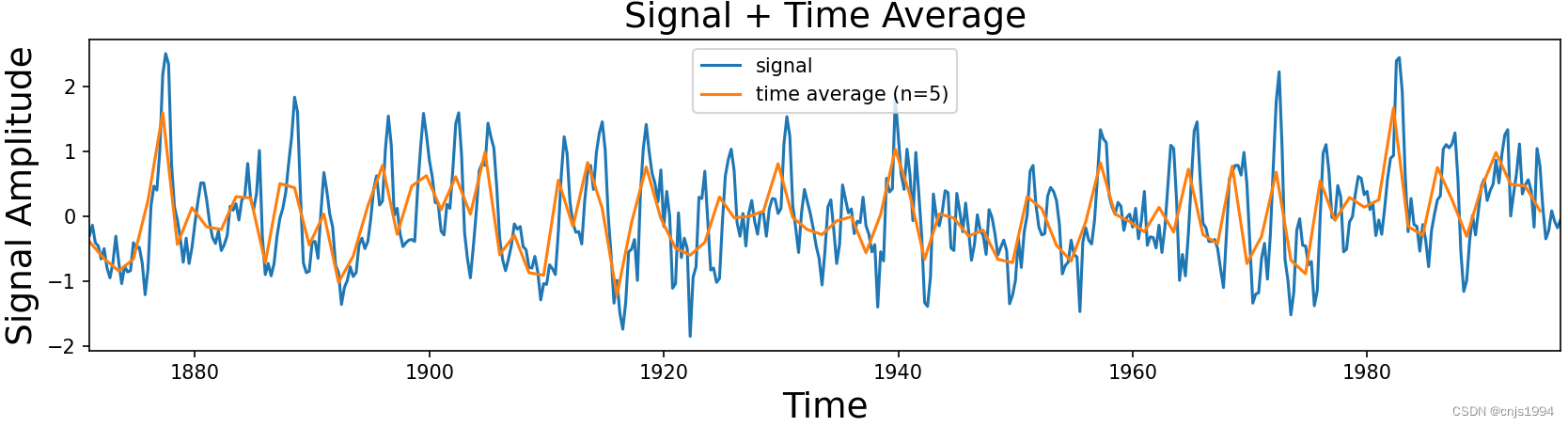
2.2 傅里叶变换结果可视化
def plot_fft_plus_power(time, signal):
dt = time[1] - time[0]
N = len(signal)
fs = 1 / dt
fig, ax = plt.subplots(figsize=(15, 3))
variance = np.std(signal) ** 2
f_values, fft_values = get_fft_values(signal, dt, N, fs)
fft_power = variance * abs(fft_values) ** 2 # FFT power spectrum
ax.plot(f_values, fft_values, 'r-', label='Fourier Transform')
ax.plot(f_values, fft_power, 'k--', linewidth=1, label='FFT Power Spectrum')
ax.set_xlabel('Frequency [Hz / year]', fontsize=18)
ax.set_ylabel('Amplitude', fontsize=18)
ax.legend()
plt.show()
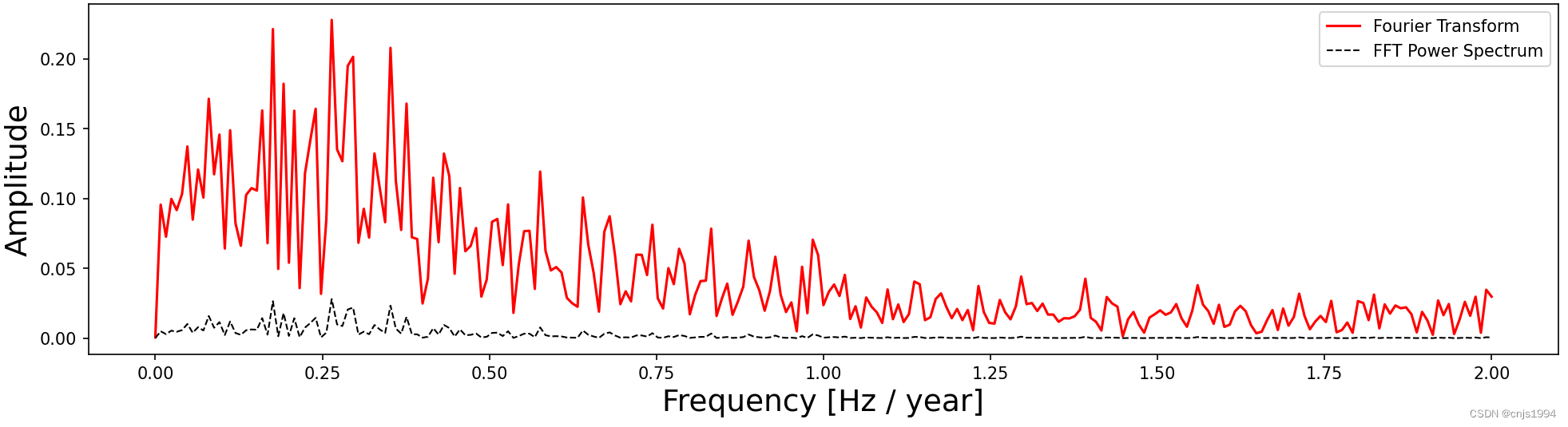
2.3 小波变换结果可视化
def plot_wavelet(time, signal, scales,
waveletname='cmor',
cmap=plt.cm.seismic,
title='Wavelet Transform (Power Spectrum) of signal',
ylabel='Period (years)',
xlabel='Time'):
dt = time[1] - time[0]
[coefficients, frequencies] = pywt.cwt(signal, scales, waveletname, dt)
power = (abs(coefficients)) ** 2
period = 1. / frequencies
levels = [0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8]
contourlevels = np.log2(levels)
fig, ax = plt.subplots(figsize=(15, 10))
im = ax.contourf(time, np.log2(period), np.log2(power), contourlevels, extend='both', cmap=cmap)
ax.set_title(title, fontsize=20)
ax.set_ylabel(ylabel, fontsize=18)
ax.set_xlabel(xlabel, fontsize=18)
yticks = 2 ** np.arange(np.ceil(np.log2(period.min())), np.ceil(np.log2(period.max())))
ax.set_yticks(np.log2(yticks))
ax.set_yticklabels(yticks)
ax.invert_yaxis()
ylim = ax.get_ylim()
ax.set_ylim(ylim[0], -1)
cbar_ax = fig.add_axes([0.95, 0.5, 0.03, 0.25])
fig.colorbar(im, cax=cbar_ax, orientation="vertical")
plt.show()
plot_wavelet(time, signal, scales)
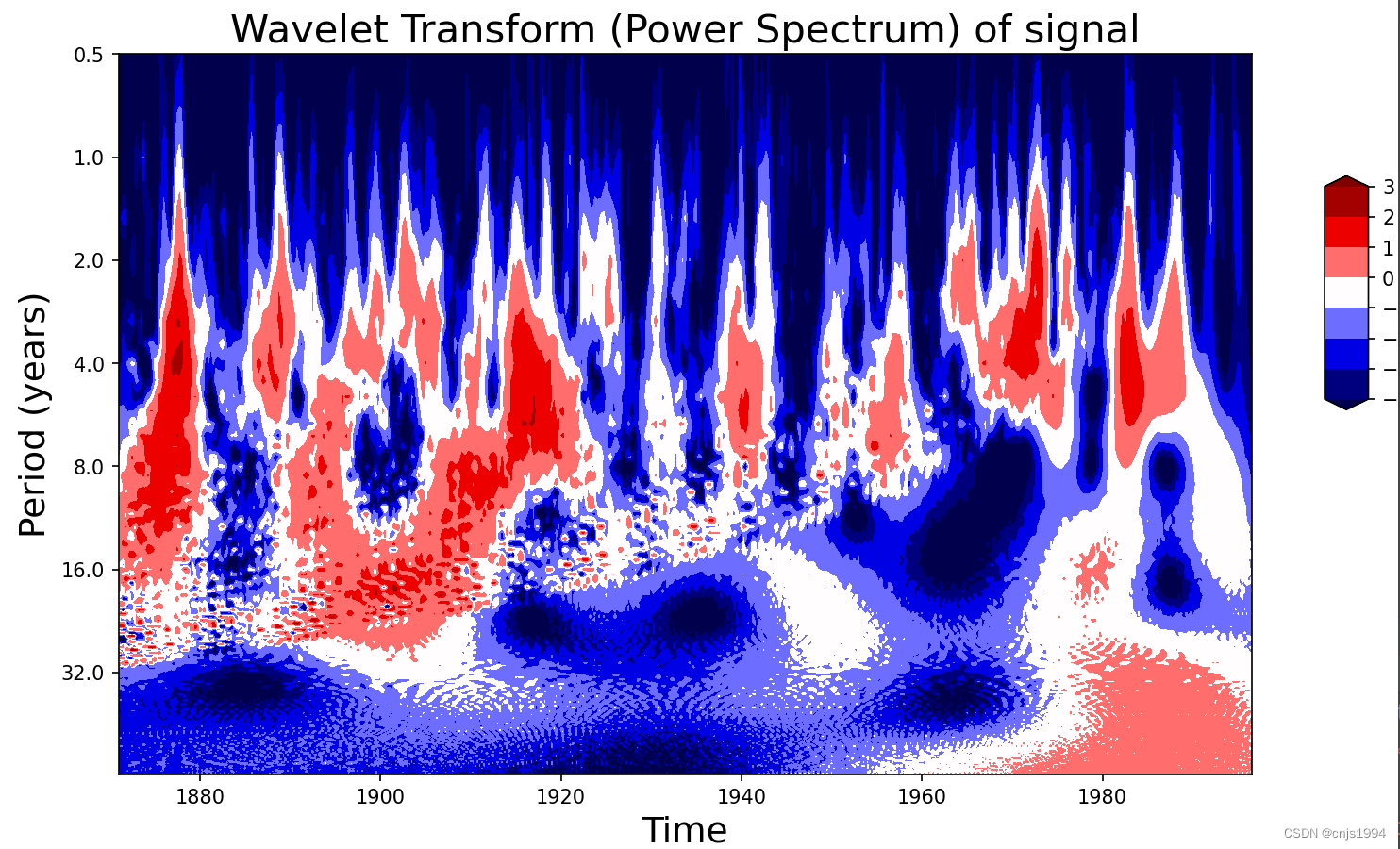
参考资料
【1】 数据集来源
后记
最后,大家希望了解的内容,欢迎评论建议!






![[go学习笔记.第十八章.数据结构] 1.基本介绍,稀疏数组,队列(数组实现),链表](https://img-blog.csdnimg.cn/d7aea688b36e4a96b8e309eccec89c71.png)