王者荣耀战区活跃度排名怎么实现的？这篇文章给你答案！

news2024/11/25 10:58:05

🍉博客主页:阿博历练记
📖文章专栏:数据结构与算法
🚍代码仓库:阿博编程日记
🍥欢迎关注:欢迎友友们点赞收藏+关注哦🌹

在这里插入图片描述

文章目录

    • 🌈前言
    • 🍪堆的实现
      • 🔍1.堆的结构框架
      • 🔍2.堆的初始化
      • 🔍3.堆的插入数据
      • 🪄向上调整算法
      • ⭐求父亲结点
      • ⭐注意break
      • ⭐while循环的条件
      • 🔍4.堆的删除数据（默认规定删除堆顶的数据）
      • 🪄向下调整算法
      • 💯假设法
      • ⭐没有右孩子
      • ⭐while循环的结束条件
      • 🍁向上调整和向下调整算法前提
      • 🔍5.堆的判空
      • 🔍6.取堆顶数据
      • ⭐注意判空
      • 🔍7.返回堆中数据的个数
      • ⭐堆插入数据和删除数据的时间复杂度
      • 🔍8.堆的销毁
      • 🎎堆排序
      • ⭐升序和降序是建小堆还是大堆
      • 🎮向下调整建堆的时间复杂度
      • 🎮向上调整建堆的时间复杂度
      • 🎮堆排序的时间复杂度
      • 🎎Topk问题
      • ⭐生成数据放在文件中
      • ⭐打印前k个最大的数据
      • ⭐第二次fscanf读写的位置
      • ⭐验证程序是否正确
      • 🍗heap.h代码
      • 🍗heap.c代码
      • 🍗test.c代码

🌈前言

堆的概念及结构：
在这里插入图片描述
堆的性质：
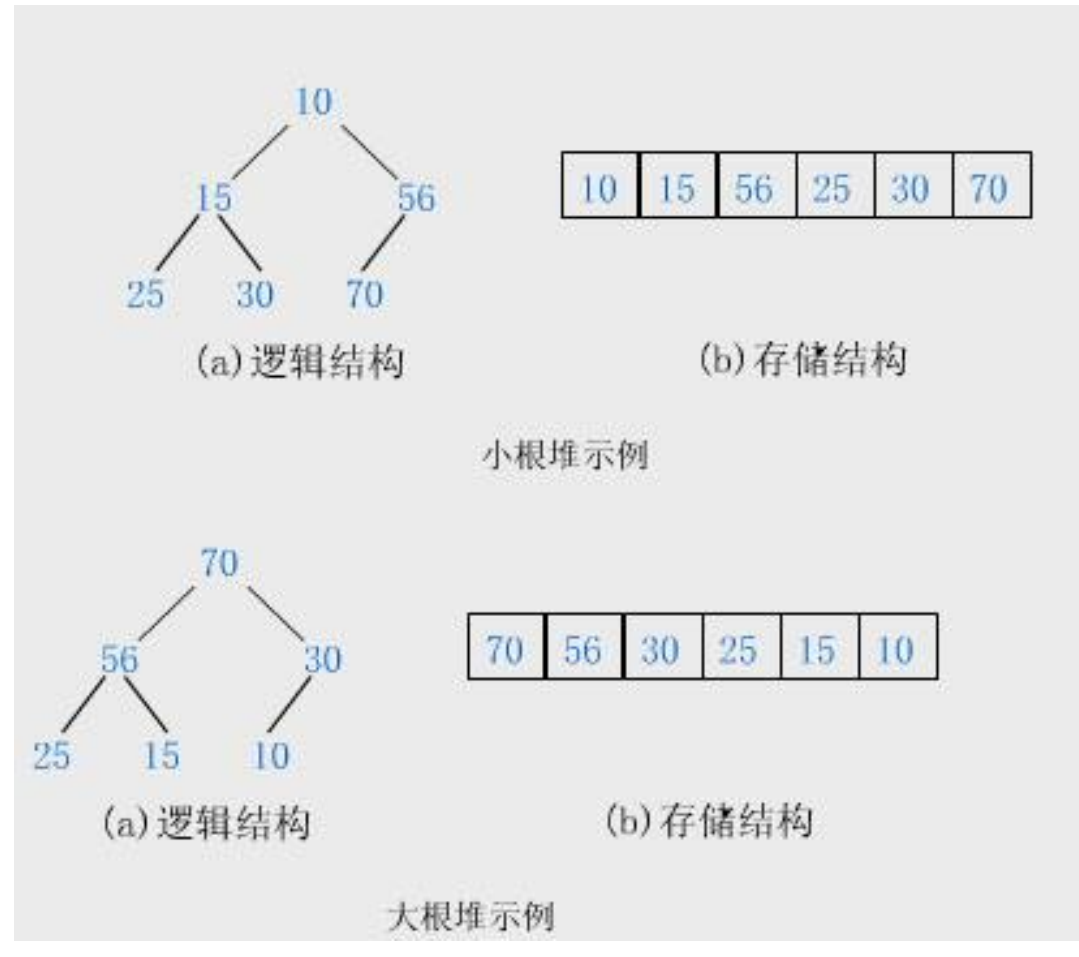
1.堆中某个节点的值总是不大于或不小于其父节点的值；
大堆：树中任何一个父亲都大于等于孩子。
小堆：树中任何一个父亲都小于等于孩子。
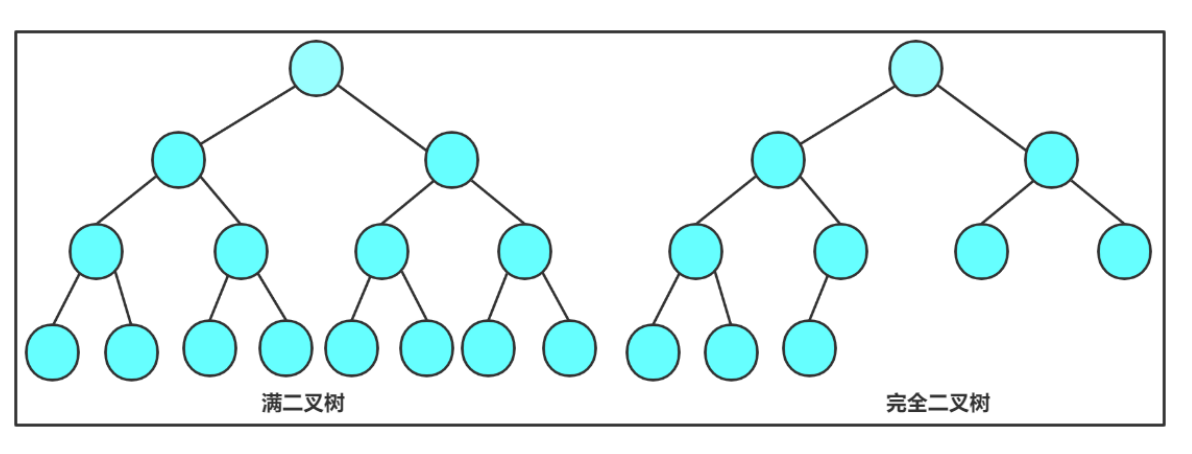
2.堆总是一棵完全二叉树。
在这里插入图片描述
🔫堆并不代表有序，因为堆只规定了父亲和孩子结点的关系，对于左右孩子结点的大小关系我们是不确定的.这里阿博给友友们介绍几个堆的应用：1.堆排序(时间复杂度是N*logN) 2.topk问题3.优先级队列

🍪堆的实现

友友们，因为堆的物理结构就是一个数组，所以这里我们的底层结构是用数组实现的.

🔍1.堆的结构框架

typedef  int  HPDataType;
typedef  struct  Heap
{
	HPDataType* a;
	int  size;
	int  capacity;
}HP;

🔍2.堆的初始化

void  HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

🔍3.堆的插入数据

void  HeapPush(HP* php,HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int  newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}

在这里插入图片描述

🪄向上调整算法

void  AdjustUp(HPDataType*a, int child)       //向上调整算法
{
	int parent = (child - 1) / 2;
	while (child>0)              //这里while循环的条件不能写成parent>=0，因为我们的parent是根本不可能小于0的，就算child来到了根结点，parent还是根节点，它还是可以进循环，逻辑不正确，这里我们的逻辑就是当孩子
	{                                 //来到根节点时，它就没有父结点了，所以此时我们终止循环，所以这里的条件是当child来到根节点时，就不要进入循环了       
		if (a[child] < a[parent])
		{
			HPDataType  tmp = a[child];
			a[child] = a[parent];                       //小堆
			a[parent] = tmp;
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

⭐求父亲结点

在这里插入图片描述

⭐注意break

在这里插入图片描述

⭐while循环的条件

友友们注意，这里while循环的条件不能写成parent>=0，因为父亲结点不会小于0，这里我们的逻辑就是当孩子结点来到根结点时就不要再进行比较了，这里如果用parent的话，当孩子结点来到根结点时，parent=(child-1)/2还是等于0，还是可以进循环，这里虽然结果不受影响，但是逻辑是不正确的，所以这里我们用child进行判断，当孩子结点来到根节点时，也就是child==0的时候，就不要再进入循环了.

🔍4.堆的删除数据（默认规定删除堆顶的数据）

void  HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	swap(&(php->a[0]), &(php->a[php->size - 1]));
	php->size--;
	AdjustDown(php->a, php->size,0) ;
}

1.挪动删除数据，重新建堆
在这里插入图片描述
2.首尾数据交换，再删除，再调堆
在这里插入图片描述

🪄向下调整算法

void  AdjustDown(int* a, int n,int parent)
{
	int child = parent * 2 + 1; 
	while (child<n)
	{
		if (child+1<n&&a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

💯假设法

友友们注意，这里用假设法，首先定义一个child为左孩子，假设左孩子是最小的，如果右孩子比左孩子小，那么child++，虽然我们不知道child是左孩子还是右孩子，但是它一定是左右孩子中最小的结点，如果没有采用这一种方法的话，我们就需要定义一个左孩子结点和右孩子结点，然后先让它们两个进行比较，最小的再和parent比较，这样就会出现代码大量的冗余.

⭐没有右孩子

在这里插入图片描述
这里友友们需要注意一下，因为堆是一个完全二叉树，它最后一层结点不是满的，但一定是连续的，所以我们需要注意一下右孩子结点不存在的情况，在比较左右孩子结点的时候，需要保证右孩子结点存在，否则就可能会出现越界访问.

⭐while循环的结束条件

友友们，这里我们的逻辑是每次向下调整的时候都需要对父亲结点和孩子结点进行比较，当孩子结点不存在的时候，我们就不需要进行比较了，也就是孩子结点的下标大于等于n，又因为堆是一颗完全二叉树，当左孩子结点不存在时，右孩子结点一定不存在，所以这里我们只需要判断左孩子结点是否存在就可以了.

🍁向上调整和向下调整算法前提

1.向上调整算法：在向上调整时，必须要保证调整前是堆
2.向下调整算法：必须要保证左右孩子是堆

🔍5.堆的判空

bool  HeapEmpty(HP* php)
{
	assert(php);
	return  php->size == 0;
}

🔍6.取堆顶数据

HPDataType  HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return   php->a[0];
}

⭐注意判空

友友们如果我们这里没有判空的话，就会出现下面三种情况：
🎲1.如果堆内有元素，那就是正常的获取堆顶元素.
🎲2.插入一个元素，再删除一个元素，此时堆已经为空了，但是如果我们没有判空的话，我们拿到的就是a[0]的数据，这就是不正确的.
🎲3.我们初始化的时候malloc了一块空间，此时堆顶的数据就是随机值.

🔍7.返回堆中数据的个数

int   HeapSize(HP* php)
{
	assert(php);
	return   php->size;
}

⭐堆插入数据和删除数据的时间复杂度

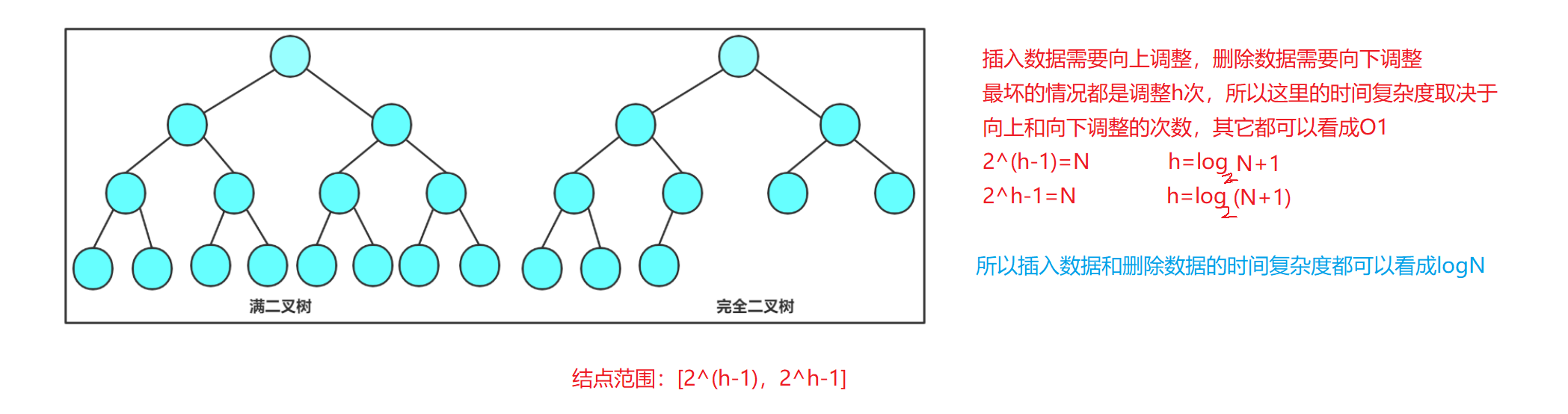
在这里插入图片描述

🔍8.堆的销毁

void  HeapDetroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

🎎堆排序

1.拷贝堆顶数据放到数组里面

void  HeapSort (int*a,int n)
{
	HP  hp;
	HeapInit(&hp);
	int  i = 0;
	for (int i = 0; i < n; i++)
	{
		HeapPush(&hp, a[i]);
	}
	while (!HeapEmpty(&hp))
	{
		a[i++] = HeapTop(&hp);          
		HeapPop(&hp);
	}
	HeapDestroy(&hp);
}

友友们，虽然这种方法可行，但是有两个弊端：1.需要先有一个堆，比较麻烦.2.空间复杂度+拷贝数据

2.对数组向上调整建堆

void  HeapSort(int* a, int n)
{
   向上调整建堆
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}
	int  end = 0;
	for (end = n; end > 1;)
	{
		swap(&a[0], &a[end-1]);
		end--;
		AdjustDown(a, end, 0);
	}
}

在这里插入图片描述

⭐升序和降序是建小堆还是大堆

在这里插入图片描述

3.对数组向下调整建堆

void  HeapSort(int* a, int n)
{
//	//向下调整建堆
	for (int i = (n-1-1)/2; i>=0; i--)
	{
		AdjustDown(a, n, i);
	}
	int  end = 0;
	for (end = n; end > 1;)
	{
		swap(&a[0], &a[end - 1]);
    	end--;
		AdjustDown(a, end, 0);
	}
}

在这里插入图片描述

🎮向下调整建堆的时间复杂度

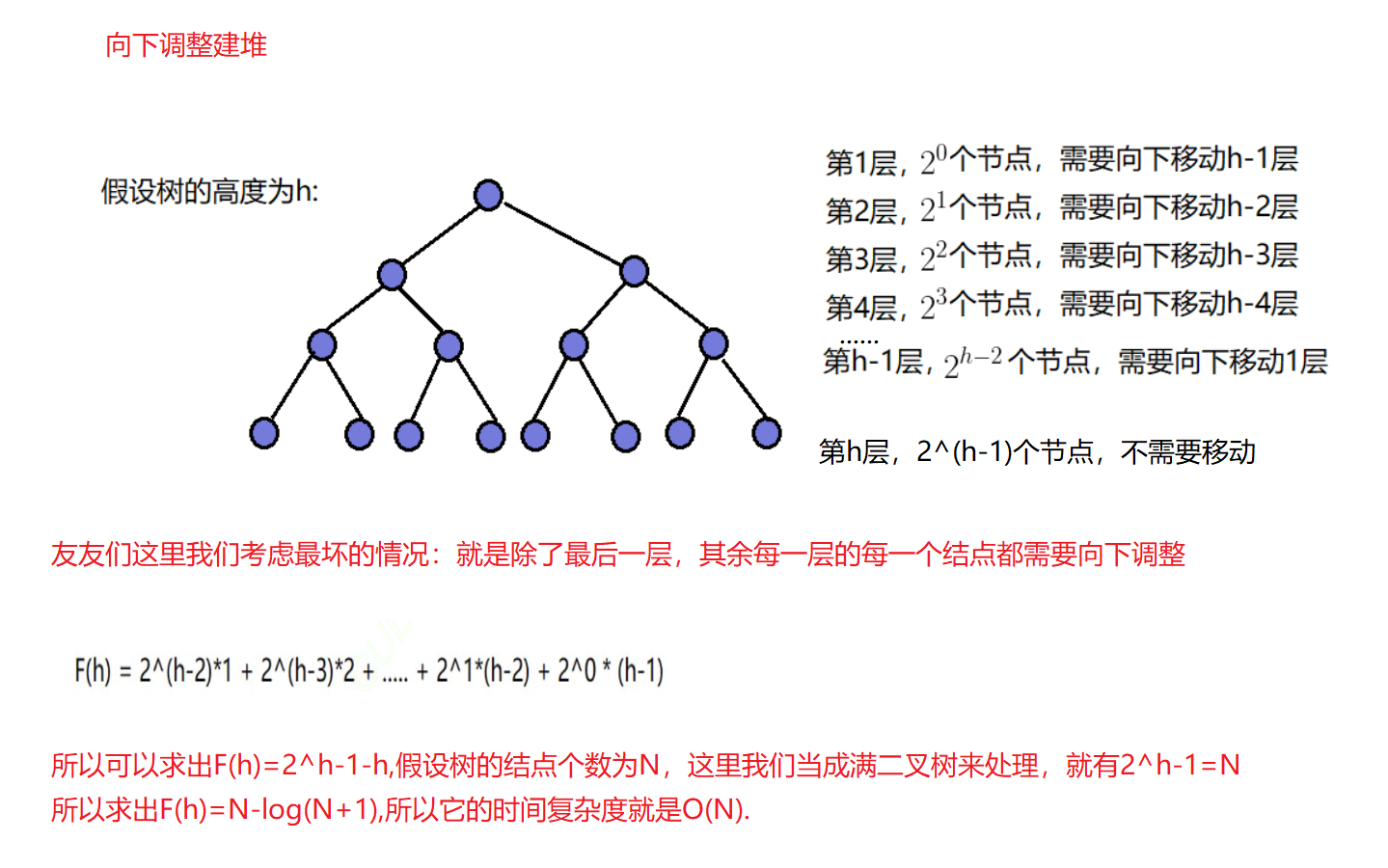
在这里插入图片描述

🎮向上调整建堆的时间复杂度

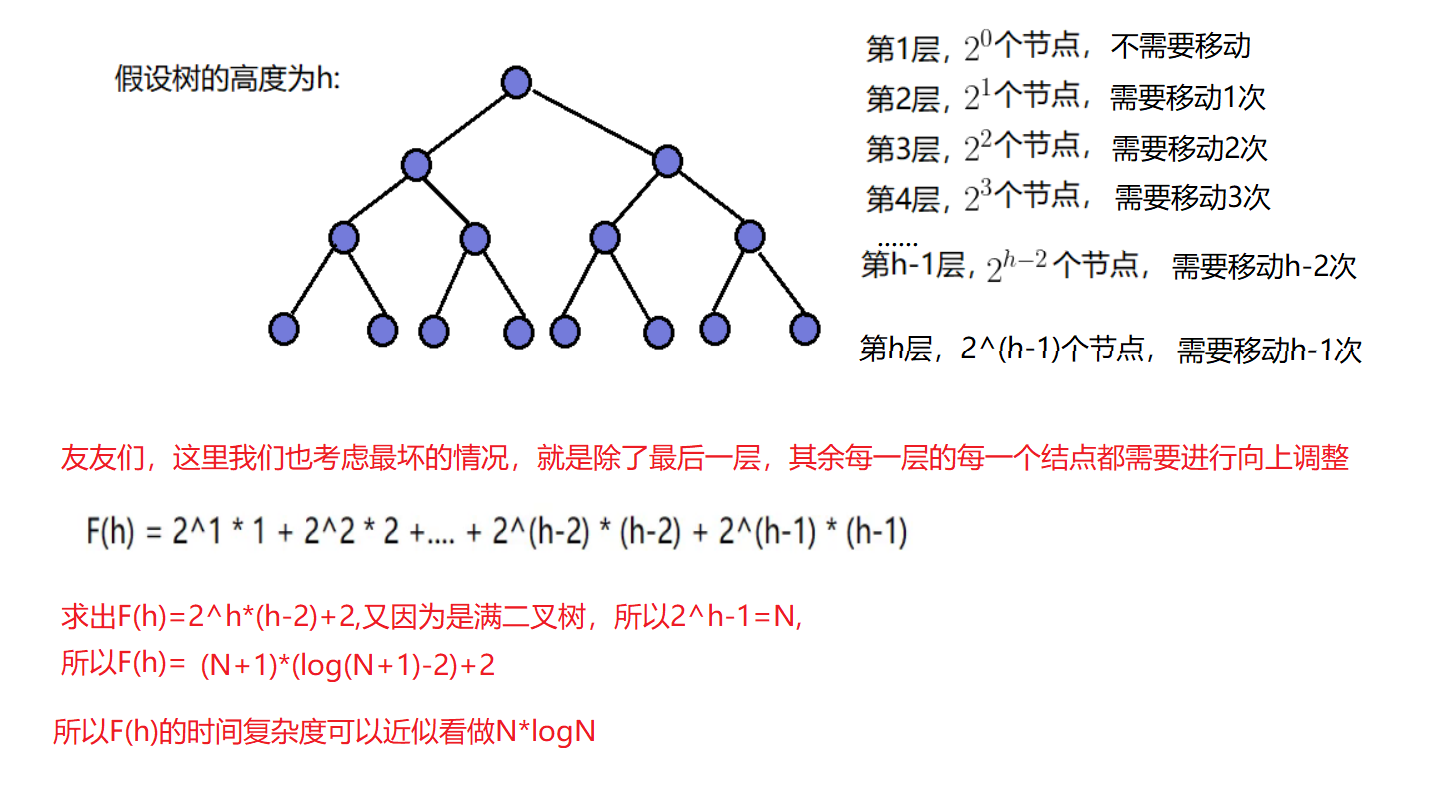
在这里插入图片描述

🎮堆排序的时间复杂度

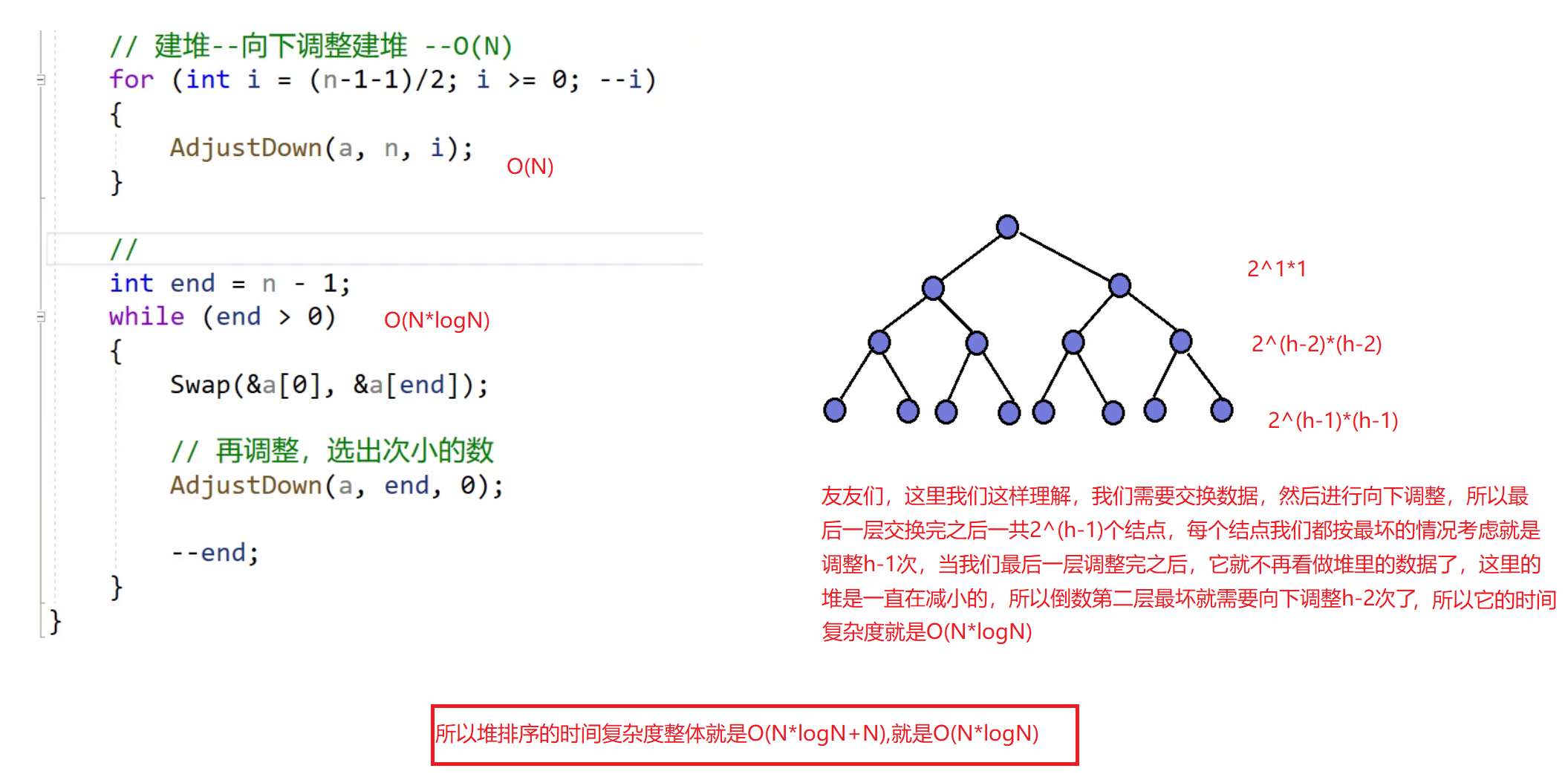
在这里插入图片描述

🎎Topk问题

⭐生成数据放在文件中

void  CreateNDate()
{
	srand((unsigned int)time(0));
	int  n = 1000;
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen  fail");
		return;
	}
	for (size_t i = 0; i < n; i++)
	{
		int x = rand()%1000000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}

⭐打印前k个最大的数据

void  PrintTopk(int k)
{
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen  fail");
		return;
	}
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc  fail");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout,"%d",&kminheap[i]);
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}
	int  value = 0;
	while (!feof(fout))
	{
		fscanf(fout,"%d",&value);                //注意这里文件指针已经不是从头开始读了，因为前面文件指针已经读取k个数据了
		if (value > kminheap[0])
		{
			swap(&value, &kminheap[0]);
			AdjustDown(kminheap, k, 0);
		}
	}
	for (int i = 0; i < 5; i++)
	{
		printf("%d ", kminheap[i]);
	}
}

在这里插入图片描述

⭐第二次fscanf读写的位置

友友们注意，第一次fscanf从文件中读取了前k个数据建小堆，文件指针来到了第k+1个位置，所以当我们建完小堆之后再次fscanf，它就会从第k+1个位置开始读数据.

⭐验证程序是否正确

友友们，这里我们无法确定我们打印的就是N个数据中最大的前K个，但是我们可以手动改变，因为我们生成的数都在1000000以内，所以我们可以写几个大于1000000的数据，如果它能打印出来，就证明我们这个程序是正确的.

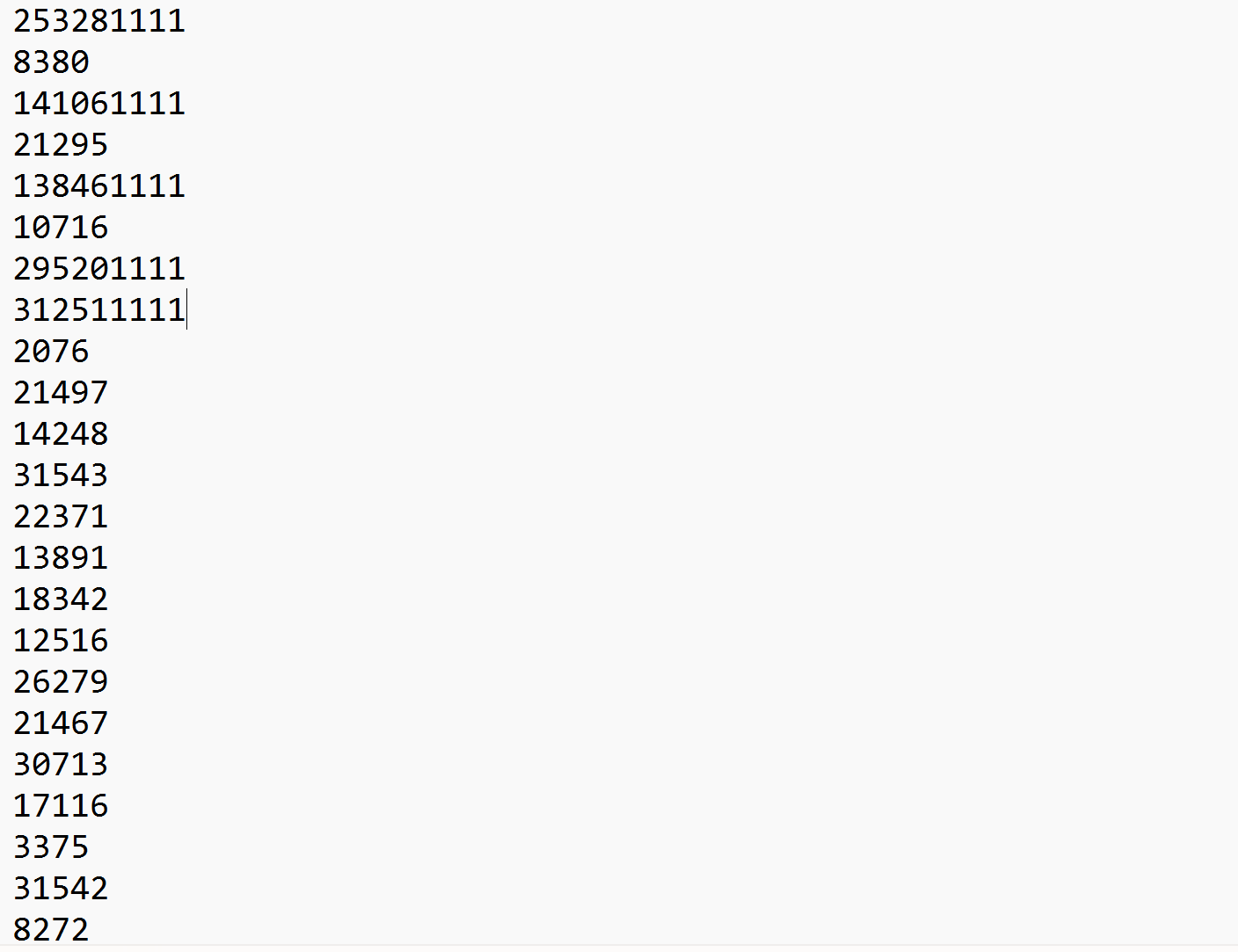
在这里插入图片描述
在这里插入图片描述

🍗heap.h代码

#pragma once
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<stdio.h>
typedef  int  HPDataType;
typedef  struct  Heap
{
	HPDataType* a;
	int  size;
	int  capacity;
}HP;
void  HeapInit(HP* php);
void  HeapDestroy(HP* php);
void  HeapPush(HP* php,HPDataType x);
void  HeapPop(HP* php);
HPDataType  HeapTop(HP* php);
bool  HeapEmpty(HP* php);
int   HeapSize(HP* php);
void  AdjustUp(int* a, int child);
void  AdjustDown(int* a, int n, int parent);
void  swap(HPDataType* p1, HPDataType* p2);

🍗heap.c代码

#define  _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void  HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}
void  HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void  AdjustUp(int*a, int child)       //向上调整算法
{
	int parent = (child - 1) / 2;
	while (child>0)              //这里while循环的条件不能写成parent>=0，因为我们的parent是根本不可能小于0的，就算child来到了根结点，parent还是根节点，它还是可以进循环，逻辑不正确，这里我们的逻辑就是当孩子
	{                                 //来到根节点时，它就没有父结点了，所以此时我们终止循环，所以这里的条件是当child来到根节点时，就不要进入循环了       
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);                              //小堆
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void  HeapPush(HP* php,HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int  newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}
void  swap(HPDataType* p1,HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void  AdjustDown(int* a, int n,int parent)
{
	int child = parent * 2 + 1; 
	while (child<n)
	{
		if (child+1<n&&a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void  HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	swap(&(php->a[0]), &(php->a[php->size - 1]));
	php->size--;
	AdjustDown(php->a, php->size,0) ;
}
HPDataType  HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return   php->a[0];
}
bool  HeapEmpty(HP* php)
{
	assert(php);
	return  php->size == 0;
}
int   HeapSize(HP* php)
{
	assert(php);
	return   php->size;
}

🍗test.c代码

#define  _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
#include<time.h>
//int  main()
//{
//	HP  hp;
//	HeapInit(&hp);
//	int  arr[] = { 65,100,70,32,50,60 };
//	for (int i = 0; i < 6; i++)
//	{
//		HeapPush(&hp, arr[i]);
//	}
//	while (!HeapEmpty(&hp))
//	{
//		printf("%d\n", HeapTop(&hp));      //有序打印，不是排序
//		HeapPop(&hp);
//	}
//	return  0;
//}
//void  HeapSort (int*a,int n)
//{
//	HP  hp;
//	HeapInit(&hp);
//	int  i = 0;
//	for (int i = 0; i < n; i++)
//	{
//		HeapPush(&hp, a[i]);
//	}
//	while (!HeapEmpty(&hp))
//	{
//		a[i++] = HeapTop(&hp);           //弊端：1.先有一个堆，太麻烦 2.空间复杂度+拷贝数据
//		HeapPop(&hp);
//	}
//	HeapDestroy(&hp);
//}
void  HeapSort(int* a, int n)
{
	向上调整建堆
	//for (int i = 1; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}
	//int  end = n;
	//while(end>1)
	//{
	//	swap(&a[0], &a[end-1]);
	//	end--;
	//	AdjustDown(a, end, 0);
	//}
	//向下调整建堆
	for (int i = (n-1-1)/2; i>=0; i--)
	{
		AdjustDown(a, n, i);
	}
	int  end = n;
	while(end>1)
	{
		swap(&a[0], &a[end - 1]);
		end--;
		AdjustDown(a, end, 0);
	}
}
void  CreateNDate()
{
	srand((unsigned int)time(0));
	int  n = 1000;
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen  fail");
		return;
	}
	for (size_t i = 0; i < n; i++)
	{
		int x = rand()%1000000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}
void  PrintTopk(int k)
{
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen  fail");
		return;
	}
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc  fail");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout,"%d",&kminheap[i]);
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(kminheap, k, i);
	}
	int  value = 0;
	while (!feof(fout))
	{
		fscanf(fout,"%d",&value);                //注意这里文件指针已经不是从头开始读了，因为前面文件指针已经读取k个数据了
		if (value > kminheap[0])
		{
			swap(&value, &kminheap[0]);
			AdjustDown(kminheap, k, 0);
		}
	}
	for (int i = 0; i < 5; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");
}
int  main()
{/*
	top问题
	10000个数中，找出最大的前十个
	建立大堆，pop9次*/
	int  a[] = { 7,8,3,5,1,9,5,4 };
	HeapSort(a, sizeof(a) / sizeof(a[0]));
	/*文件中找Topk问题*/
	//CreateNDate();
	PrintTopk(5);
	return  0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/613169.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

通过ChatGPT打造10W+公众号文章

通过ChatGPT打造10W+公众号文章

大家好&#xff0c;我是可夫小子&#xff0c;关注AIGC、读书和自媒体。解锁更多ChatGPT、AI绘画玩法。加&#xff1a;keeepdance&#xff0c;备注&#xff1a;chatgpt。 这是一篇非常具有实操性的指南&#xff0c;可能会动到一些某些行业人的蛋糕&#xff0c;但我无益于此。我是…
阅读更多...
pnpm的安装和使用

pnpm的安装和使用

1 安装 1.1 安装教程 npm全局安装pnpm npm install -g pnpm设置镜像地址 获取当前配置的镜像地址 pnpm get registry设置新的镜像地址 pnpm set registry https://registry.npm.taobao.org设置包存放地址 pnpm config set store-dir E:/xxx1.2 安装问题 当在vscode上使用…
阅读更多...
在labview里使用LabSQL连接ACCESS数据库

在labview里使用LabSQL连接ACCESS数据库

使用LabSQL连接ACCESS数据库 写在前面ODBC数据源管理器的配置LV软件里使用结束 写在前面 ACCESS数据库一般包含在Office组件里&#xff0c;安装完Office后就可以直接拿来使用&#xff0c;要求不高的场合适合使用。 LabSQL工具包直接放进LV的安装目录下&#xff0c;打开软件后在…
阅读更多...
SpringBootWeb案例-1(下： 来源黑马程序员)

SpringBootWeb案例-1(下： 来源黑马程序员)

3. 员工管理 完成了部门管理的功能开发之后&#xff0c;我们进入到下一环节员工管理功能的开发。 基于以上原型&#xff0c;我们可以把员工管理功能分为&#xff1a; 分页查询带条件的分页查询删除员工新增员工修改员工 3.1 分页查询 3.1.1 基础分页 3.1.1.1 需求分析 我…
阅读更多...
YOLOV8 Onnxruntime Opencv DNN C++部署

YOLOV8 Onnxruntime Opencv DNN C++部署

1.Opencv介绍 OpenCV由各种不同组件组成。OpenCV源代码主要由OpenCV core（核心库）、opencv_contrib和opencv_extra等子仓库组成。近些年，OpenCV的主仓库增加了深度学习相关的子仓库：OpenVINO（即DLDT, Deep Learning Deployment Toolkit）、open_model_zoo，以及标注工具CV…
阅读更多...
C++标准模板库 队列容器的使用

C++标准模板库 队列容器的使用

队列&#xff1a;在数据结构中也成为操作受限的线性表&#xff0c;是一种只允许在表的一端插入&#xff0c;在另一端删除的线性表 特点&#xff1a;先进先出&#xff0c;像打饭《排在最前面的先买&#xff0c;后到的排在队尾&#xff0c;即删除在队头&#xff0c;插入在队尾》…
阅读更多...
面试测试工程师，都要考察什么？

面试测试工程师，都要考察什么？

今年刚接触了&#xff08;功能&#xff09;测试工程师的面试工作&#xff0c;有遇到对信贷业务流程较熟悉的、工作内容纯测试app功能的、什么都接触过但是不够深入的&#xff0c;发现简历上写的东西和实际真的有点差距&#xff0c;面试也是一个艺术活。 如果你想学习自动化测试…
阅读更多...
Security Onion(安全洋葱)开源入侵检测系统(ids)安装

Security Onion(安全洋葱)开源入侵检测系统(ids)安装

文章目录 Security Onion介绍安装配置&#xff08;最低&#xff09;安装步骤web界面 Security Onion介绍 Security Onion是一款专为入侵检测和NSM(网络安全监控)设计的Linux发行版。其安装过程很简单&#xff0c;在短时间内就可以部署一套完整的NSM收集、检测和分析的套件。Se…
阅读更多...
高完整性系统（6）Alloy核心语法 + 有限状态机（Finite State Machines）；check assertion amination

高完整性系统（6）Alloy核心语法 + 有限状态机（Finite State Machines）；check assertion amination

文章目录 Alloy 核心内容sig数据类型varonefactpre-conditionfunpred 谓词谓词的构成谓词的结果 / 普通条件约束和 pre-post condition 的区别 Finite State Machines 有限状态机FSM in Alloy Check Specification动画&#xff08;Animation&#xff09;&#xff1a;run 关键字…
阅读更多...
安装superset并连接clickhouse

安装superset并连接clickhouse

说明&#xff1a; Apache Superset是一个现代的数据探索和可视化平台。它功能强大且十分易用&#xff0c;可对接各种数据源&#xff0c;包括很多现代的大数据分析引擎&#xff0c;拥有丰富的图表展示形式&#xff0c;并且支持自定义仪表盘。 使用的服务器操作系统为CentOS 7&a…
阅读更多...
路径规划算法：基于天牛须优化的路径规划算法- 附代码

路径规划算法：基于天牛须优化的路径规划算法- 附代码

路径规划算法&#xff1a;基于天牛须优化的路径规划算法- 附代码 文章目录 路径规划算法&#xff1a;基于天牛须优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要&#xff1a;本文主要介绍利用智能优化算法…
阅读更多...
【数据结构与算法篇】深入浅出——二叉树（详解）

【数据结构与算法篇】深入浅出——二叉树（详解）

​&#x1f47b;内容专栏&#xff1a;《数据结构与算法专栏》 &#x1f428;本文概括&#xff1a; 二叉树是一种常见的数据结构&#xff0c;它在计算机科学中广泛应用。本博客将介绍什么是二叉树、二叉树的顺序与链式结构以及它的基本操作&#xff0c;帮助读者理解和运用这一重…
阅读更多...
微信开发框架WxJava之微信公众号开发的入门使用篇

微信开发框架WxJava之微信公众号开发的入门使用篇

微信开发框架WxJava之微信公众号开发的入门使用篇 WxJava介绍微信公众号申请测试公众号测试公众号配置 WxJava微信公众号开发添加依赖配置微信参数实例化WxMpService对接微信公众号回调接收与回复消息 微信消息路由器WxMpMessageHandlerWxMessageInterceptor自定义Handle自定义…
阅读更多...
Vue.js devtools运行但调试窗口未出现的解决方案

Vue.js devtools运行但调试窗口未出现的解决方案

Vue.js devtools是一款基于Chrome浏览器的调试Vue.js应用的扩展程序。然而&#xff0c;有时即使该插件已经在运行&#xff0c;调试窗口也可能未出现。这主要可能有以下几个原因&#xff0c;并附有相应的解决方法&#xff1a; 1. Chrome扩展程序选项的问题 首先&#xff0c;右上…
阅读更多...
关于数据挖掘的问题之经典案例

关于数据挖掘的问题之经典案例

依据交易数据集 basket_data.csv挖掘数据中购买行为中的关联规则。 问题分析&#xff1a; 如和去对一个数据集进行关联规则挖掘&#xff0c;找到数据集中的项集之间的关联性。 处理步骤&#xff1a; 首先导入了两个库&#xff0c;pandas 库和 apyori 库。pandas 库是 Pytho…
阅读更多...
二叉树基础知识力扣题构造二叉树总结

二叉树基础知识力扣题构造二叉树总结

二叉树 如何理解二叉树&#xff0c;This is a question! 作者在去年被布置要求学习二叉树时对二叉树的理解并不是很深刻&#xff0c;甚至可以说是绕道走&#xff0c;但是Luck of the draw only draws the unlucky&#xff0c;在学期初考核时&#xff0c;作者三道二叉树题都没…
阅读更多...
ArrayBlockingQueue中方法的基本使用

ArrayBlockingQueue中方法的基本使用

生产者生产数据 使用add()方法向队列中添加元素&#xff0c;在队列满的时候会抛出异常。 ArrayBlockingQueue是基于数组实现&#xff0c;初始化完成后长度是不可变的&#xff0c;在其构造方法中也都是有参构造&#xff0c;初始化对象时必须指定当前队列的长度。 使用offer()方…
阅读更多...
day05——K-近邻算法

day05——K-近邻算法

K-近邻算法 一、定义二、API三、实操&#xff1a;预测签到位置1&#xff0c;数据获取2&#xff0c;数据基本处理3&#xff0c;预测算法代码 四、调优1&#xff0c;什么是交叉验证2&#xff0c;超参数搜索-网格搜索(Grid Search)3&#xff0c;调优代码 五、KNN 算法总结 一、定义…
阅读更多...
网工内推 | 应届生网工专场，最高15薪，有NP以上证书优先

网工内推 | 应届生网工专场，最高15薪，有NP以上证书优先

01 智己汽车 &#x1f537;招聘岗位&#xff1a;网络工程师 &#x1f537;职责描述&#xff1a; 1.管理和运维支持网络基础设备&#xff08;防火墙&#xff0c;交换机&#xff0c;路由器&#xff0c;负载均衡、无线、准入等&#xff09;&#xff1b; 2.负责公司OA网络及公有云…
阅读更多...
类和对象以及数组工具类的常用方法

类和对象以及数组工具类的常用方法

文章目录 一、类和对象二、数组工具类的常用方法 一、类和对象 1、对象没人引用时&#xff0c;会被自动回收 2、对象一定在堆上&#xff0c;引用变量不一定在栈上 3、this表示当前对象的引用&#xff0c;谁调用eat方法(eat方法里有this)&#xff0c;谁就是this。this.data访问…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023