二叉树

如何理解二叉树，This is a question!

作者在去年被布置要求学习二叉树时对二叉树的理解并不是很深刻，甚至可以说是绕道走，但是Luck of the draw only draws the unlucky，在学期初考核时，作者三道二叉树题都没做出来，连最简单的创建都忘记了，当时想着提升，却拖到了现在；

这篇文章可以说是作者二叉树算法实战经验总结

基础知识

先来回顾一下二叉树的基本知识；但还是请读者曾经是见过二叉树的

一颗很普通的二叉树，他的定义是：是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成；

其余的基本知识，还是请自行搜索一下；现在来了解几种遍历手法

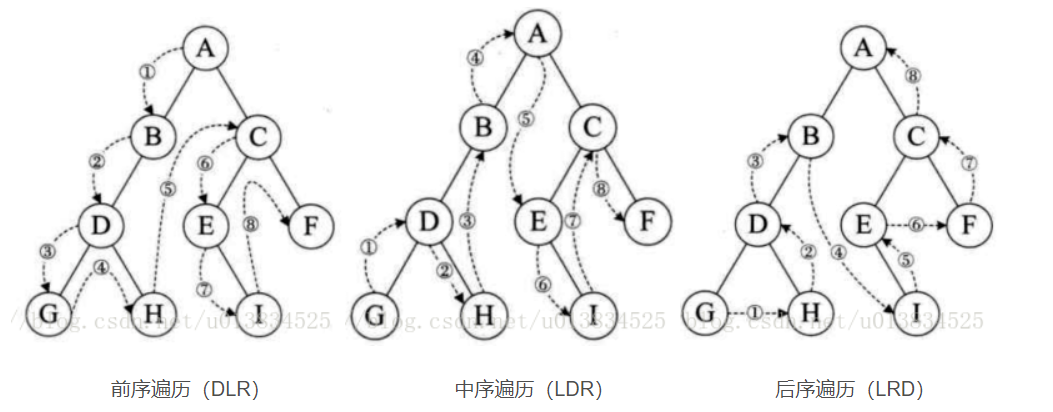
二叉树的前序遍历

 int len;
//DLR
void DFS(int*arr,struct TreeNode*root) {
     if(root == NULL) return;
     arr[len] = root->val;
     len++;
     DFS(arr,root->left);
     DFS(arr,root->right);

 }

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int*arr = (int*)malloc(sizeof(int)*100);
    len = 0;
    if(root != NULL)
        DFS(arr,root);
    *returnSize = len;
    return arr;
}

二叉树的后序遍历

int len;
//LRD
void DFS(int*arr,struct TreeNode*root) {
     if(root == NULL) return;
     DFS(arr,root->left);
     DFS(arr,root->right);
     arr[len] = root->val;
     len++;

 }

int* postorderTraversal(struct TreeNode* root, int* returnSize){
   int*arr = (int*)malloc(sizeof(int)*100);
    len = 0;
    if(root != NULL)
        DFS(arr,root);
    *returnSize = len;
    return arr;
}

二叉树的中序遍历

int len;
//LDR
void DFS(int*arr,struct TreeNode* root) {
    if(root == NULL) return;
    DFS(arr,root->left);
    arr[len] = root->val;
    len++;
    DFS(arr,root->right);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    len = 0;
    int*arr = (int*)malloc(sizeof(int)*100);
    if(root != NULL) {
        DFS(arr,root);
    }
    *returnSize = len;
    return arr;
}

在三种遍历方法中，我们都采用了递归的方法，而仔细观察也会发现，这三段代码的区别，从字面上仅是递归函数的位置不同，也就是遍历时的顺序不同，这个也就是我们在解决二叉树算法题时要注意的点，不同的遍历方式对应着不同的类型的解决方案

在这三种遍历代码前，都标注了三个大写字母，D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树，会发现字母的顺序也就代表着优先级也就是代码呈现的顺序；

如何理解这种遍历手法，以前序遍历为例，他的三个字母顺序为DLR，也就是根节点最优先，自然就是A，之后就到B，C这两个在这里判断的条件就成了谁左谁优先，也就是B先行，B的底下还有子树，坚持D最优先原则，由于他们有一个优秀的父结点，因为所有都可以得到先行一步的遍历权利，等到遍历完了也就是在轮到C和C的子树；

总结就是：坚持大方向，父结点优先，子结点也继承了优先权

那么基础知识就讲到这里，接下来实战演练

实战演练

104.二叉树的最大深度

这是一道非常基础的题目，也就是再问一根树枝最长能有多长，也就是遍历出奇迹

第一种方法：回溯

（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”

对这种算法的解释就是：一条道走到黑，且要走完每条道

先看代码：

class Solution {
    int depth = 0;
    int res = 0;

    public int maxDepth(TreeNode root) {
        traverse(root);
        return res;
    }

    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        depth++;
        // 遍历的过程中记录最大深度
        res = Math.max(res, depth);
        traverse(root.left);
        traverse(root.right);
        depth--;
    }
}

对代码的唯一不理解的地方应该是为何要先depth++之后又depth--，我们可以把整个函数理解为一个在四处游走的图钉，当图钉到这个点上了，depth++，现在我小图钉在这里一条道走到黑要离开去其他地方了，那么则先depth--，因为回到更上面一层去了；这跟前序遍历很像

至于res的取值，只要放在depth--之前就行了

第二种方法：动态规划

class Solution2 {
    // 定义：输入一个节点，返回以该节点为根的二叉树的最大深度
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        // 根据左右子树的最大深度推出原二叉树的最大深度
        return 1 + Math.max(leftMax, rightMax); //+1的原因：算上根节点
    }
}

代码很好理解，但是作者自己想不出来；思想很简单，也是遍历然后最后得出最大值，这个顺序相当于在后序遍历

543.二叉树的直径

其实这道题跟上面一道题非常像，作者对这道题的解读就是：从根节点出发第一长的树枝和第二长的树枝长度和；那么这道题也就迎刃而解了，只要在上一题的第二种解法种稍加修改，添加一个max记录值，便可以做出该题

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int maxDiameter = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxDiameter;
    }
    
    int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        int myDiameter = leftMax + rightMax;
        maxDiameter = Math.max(myDiameter, maxDiameter);
        return 1 + (Math.max(leftMax, rightMax));
    }
}

116.填充每个节点的下一个右侧指针节点

这道题的神奇之处就在于，把不是一个父结点，但是在同一层的联系在了一起，那么只要把相对位置是left&right的都链接在一起，也就是多加一条执行语句traverse(node1.right, node2.left)即可

class Solution {
    public Node connect(Node root) {
        if(root == null) {
            return null;
        }
        traverse(root.left, root.right);
        return root;
    }
    void traverse(Node node1, Node node2) {
        if(node1 == null || node2 == null) {
            return;
        }
        node1.next = node2;
        traverse(node1.left, node1.right);
        traverse(node2.left, node2.right);
        traverse(node1.right, node2.left);
    }
}

105.从前序与中序遍历序列构造二叉树

它使用HashMap来存储中序遍历数组中值到索引的映射关系，这有助于确定根节点并将数组划分为子树以进行递归构建。
buildTree 方法接受前序遍历和中序遍历数组作为输入，并通过将中序遍历数组中的值和索引存储在 valToIndex HashMap 中来进行初始化。然后，它调用 build 方法，传递必要的参数来构建二叉树。
build 方法是一个递归函数，用于构建二叉树。它检查子树是否为空（preStart > preEnd），如果是则返回null。否则，它从前序遍历数组中确定根节点的值（preorder[preStart]），并找到它在中序遍历数组中的索引。然后，它计算左子树的大小（index - inStart），并先构造当前根节点。接下来，它递归构建左子树和右子树，并将它们连接到根节点。最后，它返回根节点

class Solution {
    // 存储 inorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }

    /*
       定义：前序遍历数组为 preorder[preStart..preEnd]，
       中序遍历数组为 inorder[inStart..inEnd]，
       构造这个二叉树并返回该二叉树的根节点
    */
    TreeNode build(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
        if (preStart > preEnd) {
            return null;
        }

        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // rootVal 在中序遍历数组中的索引
        int index = valToIndex.get(rootVal);
        int leftSize = index - inStart;

        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, index - 1);
        root.right = build(preorder, preStart + leftSize + 1, preEnd, inorder, index + 1, inEnd);
        return root;
    }
}

106.从中序与后序遍历序列构造二叉树

class Solution {
    // 存储 inorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
    }

    /*
       定义：
       中序遍历数组为 inorder[inStart..inEnd]，
       后序遍历数组为 postorder[postStart..postEnd]，
       构造这个二叉树并返回该二叉树的根节点
    */
    TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {

        if (inStart > inEnd) {
            return null;
        }
        // root 节点对应的值就是后序遍历数组的最后一个元素
        int rootVal = postorder[postEnd];
        // rootVal 在中序遍历数组中的索引
        int index = valToIndex.get(rootVal);
        // 左子树的节点个数
        int leftSize = index - inStart;
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(inorder, inStart, index - 1, postorder, postStart, postStart + leftSize - 1);
        root.right = build(inorder, index + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);
        return root;
    }
}

889.根据前序与后序遍历构造二叉树

class Solution {
    // 存储 postorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        for (int i = 0; i < postorder.length; i++) {
            valToIndex.put(postorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1, postorder, 0, postorder.length - 1);
    }

    // 定义：根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
    // 构建二叉树，并返回根节点。
    TreeNode build(int[] preorder, int preStart, int preEnd, int[] postorder, int postStart, int postEnd) {
        if (preStart > preEnd) {
            return null;
        }
        if (preStart == preEnd) {
            return new TreeNode(preorder[preStart]);
        }

        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // root.left 的值是前序遍历第二个元素
        // 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
        // 确定 preorder 和 postorder 中左右子树的元素区间
        int leftRootVal = preorder[preStart + 1];
        // leftRootVal 在后序遍历数组中的索引
        int index = valToIndex.get(leftRootVal);
        // 左子树的元素个数
        int leftSize = index - postStart + 1;

        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        // 根据左子树的根节点索引和元素个数推导左右子树的索引边界
        root.left = build(preorder, preStart + 1, preStart + leftSize, postorder, postStart, index);
        root.right = build(preorder, preStart + leftSize + 1, preEnd, postorder, index + 1, postEnd - 1);

        return root;
    }
}