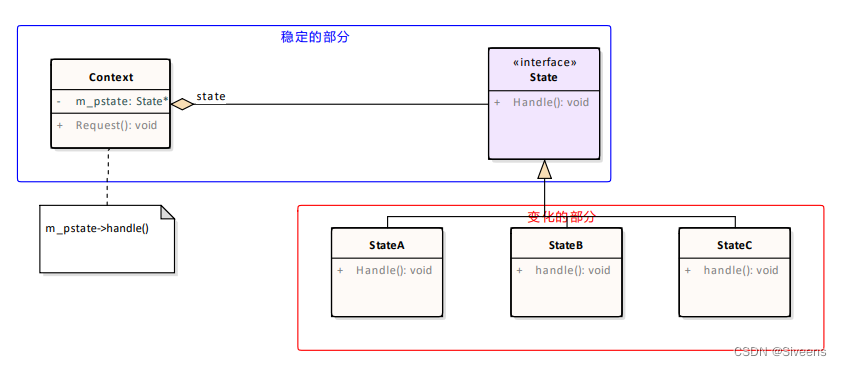
集成学习
集成学习通过构建并结合多个学习器来完成学习任务
集成方法是用多种学习方法的组合来获取比原方法更优的结果
使用于组合的算法是弱学习算法
即分类正确率仅比随机猜测略高的学习算法
但是组合之后的效果仍可能高于强学习算法
即集成之后的算法准确率和效率都很高
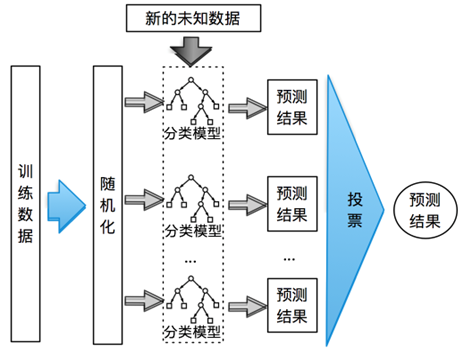
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类:
1)个体学习器间存在强大依赖关系、必须串行生成的序列化方法,代表算法:Boosting;
2)个体学习器间不存在依赖关系、可同时生成的并行化方法,代表算法Bagging和RF

装袋法(Bagging)

装袋法(Bagging)其原理是通过组合多个训练集的分类结果来提升分类效果
装袋法由于多次采样,每个样本被选中的概率相同,因此噪声数据的影响下降,所以装袋法太容易受到过拟合的影响
对于回归树:Bagging的结果就是B个没有经过Prune(剪枝)树的结果平均值。
对于分类树:我们通过Majority Vote,多数投票制,计算大多数模型认为结果应当属于哪一类,Bagging认为多数的结果是最终的分类结果。
Bagging的优缺点
Bagging提高了模型的准确率,降低了模型的Variance。
由于模型在最后用了平均值,因此Bagging结果的可解释性降低了。
提升法(Boosting)
提升法(Boosting)与装袋法相比每次的训练样本均为同一组,并且引入了权重的概念,给每个单独的训练样本都会分配个相同的初始权重。
然后进行T轮训练,每一轮中使用一个分类方法训练出一个分类模型,使用此分类模型对所有样本进行分类并更新所有样本的权重:分类正确的样本权重降低,分类错误的样本权重增加,从而达到更改样本分布的目的。
由此可知,每一轮训练后,都会生成一个分类模型,而每次生成的这个分类模型都会更加注意在之前分类错误的样本,从而提高样本分类的准确率。对于新的样本,将T轮训练出的T个分类模型得出的预测结果加权平均,即可得出最终的预测结果。
AdaBoost VS Bagging:
标准AdaBoost只适用于二分类任务,Bagging适用于多分类、回归等任务。
梯度提升决策树(GBDT)
梯度提升决策树算法是利用梯度下降的思想,使用损失函数的负梯度在当前模型的值,作为提升树中残差的近似值,以此来拟合回归决策树。梯度提升决策树的算法过程如下:
1、初始化决策树,估计一个使损失函数最小化的常数构建一个只有根节点的树;
2、不断提升迭代:
计算当前模型中损失函数的负梯度值,作为残差的估计值;
估计回归树中叶子节点的区域,拟合残差的近似值;
利用线性搜索估计叶子节点区域的值,使损失函数极小化;
更新决策树;
3、经过若干轮的提升法迭代过程之后,输出最终的模型;
随机森林(RF)
随机森林是专为决策树分类器设计的集成方式,是装袋法的一种拓展。
随机森林与装袋法采取相同的样本抽取方式。装袋法中的决策树每次从所有属性中选取一个最优的属性作为其分支属性,而随机森林算法每次从所有属性中随机抽取 t 个属性,然后从这 t 个属性中选取一个最优的属性作为其分支属性,这样就使得整个模型的随机性更强,从而使模型的泛化能力更强。
随机森林是一种有监督学习算法,是以CART决策树为基学习器的集成学习算法。随机森林非常简单,易于实现,计算开销也很小,在分类和回归上表现出非常惊人的性能,因此,随机森林被誉为“代表集成学习技术水平的方法”。

可以很明显地看到,随着随机森林中决策树数量的增多,模型的泛化能力逐渐增强,决策边界越来越趋于平滑(受到噪声点的影响越来越小)。

(1)RF划分时考虑的最大特征数(max_features)
总数的百分比,常见的选择区间是[0.5, 0.9]。
(2)决策树的棵树(n_estimators)
可能会设置为>50的取值,可根据计算资源调整。
(3)决策树最大深度(max_depth)
常见的选择在4-12之间。
(4)内部节点再划分所需最小样本数(min_samples_split)
如果样本量不大,不需要调整这个值。
如果样本量数量级非常大,我们可能会设置这个值为16,32,64等。
(5)叶子节点最少样本数(min_samples_leaf)
为了提高泛化能力,我们可能会设置这个值>1。