所需先验知识(没有先验知识可能会有大碍,了解的话会对D*的理解有帮助):A*算法/ Dijkstra算法
何为D*算法
Dijkstra算法是无启发的寻找图中两节点的最短连接路径的算法,A*算法则是在Dijkstra算法的基础上加入了启发函数h(x),以引导Dijkstra算法搜索过程中的搜索方向,让无必要搜索尽可能的少,从而提升找到最优解速度。这两者都可应用于机器人的离线路径规划问题,即已知环境地图,已知起点终点,要求寻找一条路径使机器人能从起点运动到终点。

但是上述两个算法在实际应用中会出现问题:机器人所拥有的地图不一定是最新的地图,或者说,机器人拥有的地图上明明是可以行走的地方,但是实际运行时却可能不能走,因为有可能出现有人突然在地上放了个东西,或者桌子被挪动了,或者单纯的有一个行人在机人运行时路过或挡在机器人的面前。

碰到这样的问题,比如机器人沿着预定路径走到A点时,发现在预先规划的路径上,下一个应该走的点被障碍物挡住了,这种情况时,最简单的想法就是让机器人停下来,然后重新更新这个障碍物信息,并重新运行一次Dijkstra算法 / A*算法,这样就能重新找到一条路。
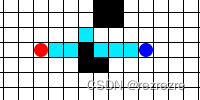
但是这样子做会带来一个问题:重复计算。假如如下图所示新的障碍物仅仅只是挡住了一点点,机器人完全可以小绕一下绕开这个障碍物,然后后面的路径仍然按照之前规划的走。可是重复运行Dijkstra算法 / A*算法时却把后面完全一样的路径重新又计算了一遍
D*算法的存在就是为了解决这个重复计算的问题,在最开始求出目标路径后,把搜索过程的所有信息保存下来,等后面碰到了先验未知的障碍物时就可以利用一开始保存下来的信息快速的规划出新的路径。
顺便一提因为D*算法有上述的特性,所以D*算法可以使用在“无先验地图信息/先验地图信息不多的环境中的导航”的问题,因为只需要在最开始假装整个地图没有任何障碍,起点到终点的路径就是一条直线,然后再在在线运行时不断使用D*算法重新规划即可。
D*算法流程
先说明一下需要用到的类,开始运行前需要对地图中每个节点创建一个state类对象,以便在搜索中使用。
# 伪代码
class state:
# 存储了每个地图格子所需的信息,下面会说到这个类用在哪。以下为类成员变量
x # 横坐标
y # 纵坐标
t = "new" # 记录了当前点是否被搜索过(可为“new”,"open", "close",分别代表这个格子没被搜索过,这个格子在open表里,这个格子在close表里。关于什么是open表什么是close表,建议去看A*算法,能很快理解)。初始化为new
parent = None # 父指针,指向上一个state,沿着某个点的父指针一路搜索就能找到从这个点到目标点end的最短路径
h # 当前代价值(D*算法核心)
k # 历史最小代价值(D*算法核心,意义是所有更新过的h之中最小的h值)
d*算法主代码:
function Dstar(map, start, end):
# map:m*n的地图,记录了障碍物。map[i][j]是一个state类对象
# start:起点,state类对象
# end: 终点,state类对象
open_list = [ ] # 新建一个open list用于引导搜索
insert_to_openlist(end,0, open_list) # 将终点放入open_list中
# 第一次搜索,基于离线先验地图找到从起点到终点的最短路径,注意从终点往起点找
loop until (start.t == “close”):process_state() # D*算法核心函数之一
end loop
# 让机器人一步一步沿着路径走,有可能在走的过程中会发现新障碍物
temp_p = start
while (p != end) do
if ( unknown obstacle found) then # 发现新障碍物, 执行重规划
for new_obstacle in new_obstacles: # 对每个新障碍物调用modify_cost函数
modify_cost( new_obstacle ) #(D*算法核心函数之一)
end for
do
k_min = process_state()
while not ( k_min >= temp_p.h or open_list.isempty() )continue
end if
temp_p = temp_p.parent
end while
上述伪代码中核心函数为2个:modify_cost 和 process_state。我翻阅了csdn几个关于process_state的解释,发现都有挺大的错误,会让整个算法在某些情况下陷入死循环(比如D*规划算法及python实现_mhrobot的博客-CSDN博客)。而且就连原论文的伪代码都有点问题(可能原论文(Optimal and Effificient Path Planning for Partially-Known Environments,
function modify_cost( new_obstacle ):
set_cost(any point to new_obstacle ) = 10000000000 # 让“从任何点到障碍点的代价”和“从障碍点到任何点的代价” 均设置为一个超大的数(考虑8邻接)
if new_obstacle.state == "close" then
insert(new_obstacle, new_obstacle.h ) # 放到open表中,insert也是d*算法中的重要函数之一
end if
下面是 Process_state函数的伪代码,注意标红那条
function process_state( ):
x = get_min_k_state(oepn_list) # 拿出openlist中获取k值最小那个state,这点目的跟A*是一样的,都是利用k值引导搜索顺序,但注意这个k值相当于A*算法中的f值(f=g+h, g为实际代价函数值,h为估计代价启发函数值),而且在D*中,不使用h这个启发函数值, 仅使用实际代价值引导搜索,所以其实硬要说,D*更像dijkstra,都是使用实际代价引导搜索而不用启发函数缩减搜索范围,D*这点对于后面发现新障碍物进行重新规划来说是必要的。
if x == Null then return -1
k_old = get_min_k(oepn_list) # 找到openlist中最小的k值,其实就是上面那个x的k值
open_list.delete(x) # 将x从open list中移除, 放入close表
x.state = "close" # 相当于放入close表,只不过这里不显式地维护一个close表
# 以下为核心代码:
# 第一组判断
if k_old < x.h then # 满足这个条件说明x的h值被修改过,认为x处于raise状态
for each_neighbor Y of X: #考虑8邻接neighbor
if y.h<k_old and x.h> y.h + cost(y,x) then
x.parent = y
x.h = y.h + cost(x,y)
end if
end for
end if
# 第二组判断
if k_old == x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y))
end if
end for
else: # 不满足k_old == x.h 那就是k_old < x.h
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) then
y.parent = x
insert(y, x.h + cost(x,y))
else:
if (y.parent != x and y.h >x.h + cost(x,y)) then
x.k = x.h # 注意这行!没有这行会出现特定情况死循环。在查阅大量资料后,在wikipedia的d*算法页面中找到解决办法就是这行代码。网上大部分资料,包括d*原始论文里都是没这句的,不知道为啥
insert(x, x.h)
else:
if (y.parent!=x and x.h>y.h+cost(y,x) and y.parent = "close" and y.h>k_old then
insert(y,y.h)
end if
end if
end if
end for
end if
return get_min_k(oepn_list)
上面使用到的insert函数:
function insert(state, new_h)
if state.t == "new": # 将未探索过的点加入到open表时,h设置为传进来的 new_h state.k = h_new # 因为未曾被探索过,k又是历史最小的h,所以k就是new_h elif state.t == "open": state.k = min(state.k, h_new) # 保持k为历史最小的h elif state.t == "close": state.k = min(state.k, h_new) # 保持k为历史最小的h state.h = h_new # h意为当前点到终点的代价 state.t = "open" # 插入到open表里所以状态也要维护成open open_list.add(state) # 插入到open表
以上便是完整的d*算法流程。
D*流程详解
现在我们从“d*算法主代码”开始详解d*函数:
第一次搜索
首先可以看到,在最开始我们需要创建一个open list,然后将终点end加入到open list,之后不断调用process_state直到起始点start被加入到close表。open表中的东西要按照k值大小排序,每次调用process_state需要取出k值最小的一个来扩展搜索,注意open list中的东西要按照 k 值大小从小到大排序而不是h值。
第一次搜索时,对应主代码中的:
# 第一次搜索,基于离线先验地图找到从起点到终点的最短路径,注意从终点往起点找
loop until (start.t == “close”):process_state() # D*算法核心函数之一
end loop
这部分。
其实,在首次搜索时,我们可以发现每个点第一次被加入到open表中时都是从new状态加入,即每次调用insert函数时state.t 最开始都是new,所以其h值与k值其实是相等的;在搜索过程中,也即每一步调用process_state时,k_old 也一直等于x.h(k_old相当于x.k),因此每次第一组判断都不会被执行,第二组判断也总是只执行k_old == x.h这部分:
# 第二组判断
if k_old == x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y))
end if
end for
else:
........
而这部分中,对x的8邻接点y的判断只会有两种情况,①y.state == "new" ②y.parent != x and y.h >x.h + cost(x,y)。而第三种情况③y.parent == x and y.h !=x.h + cost(x,y) 在这时是不会出现的,因为h的意思是当前点到终点的代价,parent的意思是最短路径上当前点到终点的路径的上一个点,那么只要某个点的parent是x,那么这个点的h一定是x的h值加上从x到这个点的代价。第三种情况出现必定是因为y.h、x.h或者cost(x,y)被非正常流程中人为修改过。
也就是说,在初次搜索时其实整个process_state代码相当于如下(因为其他部分此时不会被调用):
function process_state****(初次搜索时等价于如下函数)( ):
x = get_min_k_state(oepn_list)
if x == Null then return -1
k_old = get_min_k(oepn_list)
open_list.delete(x)
x.state = "close"
# 第二组判断
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y))
end if
end for
return get_min_k(oepn_list)
可以发现,其实这就是dijkstra算法。
实际上,d*算法在初步规划时,完全退化成了dijkstra算法,也就是说如果沿着规划出来的路径运动过程中不发生障碍物变化的话,其实d*效率是要比a*低的,因为d*并没有启发式地往目标去搜索,搜索空间实际上比a*大很多。
但是d*这么做主要是为了提高在重规划时的效率,因为dijkstra算法其实实现的是“找到某个点到空间内所有点的最短路径”(注意我们是从终点开始往起点搜索的,所以找到的就是全部点到终点的最短路径)(其实也不是全部点,因为找到起点之后就停止搜索了,没搜完的都还留在open表中,也就是最短路程大于从起点到终点距离的点都没被搜。),在运行过程中碰到障碍物需要重规划时,我们就不再需要从当前点重新搜索到终点,而是找出一条路径,让我们绕开障碍物,到达附近没有障碍物的空闲点即可,而到达这个空闲点之后的路径不需要重新搜索,因为根据初次搜索,这个空闲点到目的地的最短路径我们已经有了。
重规划
接下来我们继续看主代码,第一次搜索完之后的部分(该程序默认第一次搜索能找到解,第一次无解的话就没有重规划了所以不考虑奥):
# 让机器人一步一步沿着路径走,有可能在走的过程中会发现新障碍物
temp_p = start
while (p != end) do
if ( unknown obstacle found) then # 发现新障碍物
for new_obstacle in new_obstacles: # 对每个新障碍物调用modify_cost函数
modify_cost( new_obstacle ) #(D*算法核心函数之一)
end for
do
k_min = process_state()
while not ( k_min >= temp_p.h or open_list.isempty() )continue
end if
temp_p = temp_p.parent
end while
这里让temp_p = start然后每一步都让temp_p = temp_p.partent是为了模拟机器人沿着路径一步步走的情形。当走到中途通过传感器发现了新的障碍物时,首先将发现的新障碍物信息加入到已知地图中,即执行:
for new_obstacle in new_obstacles: # 对每个新障碍物调用modify_cost函数
modify_cost( new_obstacle ) #(D*算法核心函数之一)
end for
对每个新发现的障碍物点调用 modify_cost(注意,d*无法处理某个点本来是障碍物,现在发现它不再是障碍物的情况,不考虑它,只考虑新增障碍物)
function modify_cost( new_obstacle ):
set_cost(any point to new_obstacle ) = 10000000000
if new_obstacle.state == "close" then
insert(new_obstacle, new_obstacle.h ) # 放到open表中
end if
return
首先将障碍物到周围所有点的移动代价设为无穷大。然后,如果
- 新发现的障碍物点状态是“new”,那就不用管,因为等一下执行process_state时,new点被第一次加入open表中时,这个无穷大的代价就会体现在其周围的点的h值上。实际上,如果一个点在重规划时还在new中的话,证明这个点第一次搜索并没有利用到它的信息,所以它在这次搜索过程中并不算“新成为障碍物”,因为第一次搜索时根本都不知道它是不是障碍物;
- 如果这个点的状态是“open”,也即这个点在open表中,那么也不用管,因为在open表中等下运行process_state时会被展开,然后其障碍信息会通过cost(x,y)这一项传递给周围的点。(障碍物点本身的h值不是无穷并没有关系,因为虽然这样做的话障碍物点本身能找到通往终点的路径,但是障碍物点本身并不会被机器人占领,所以不用担心。);
- 如果这个点的状态是close,那就将其原封不动(也即不用修改其h值)地移入open表,待等下执行process_state时将其障碍信息通过cost传递给附近的点即可;
在将新变成障碍物的点放入open表中后(new 的点也总归会被加入open表,如果没被加入那证明不需要它),就开始重复执行process_state, 直到找到解或者无解,即这段代码:
do
k_min = process_state()
while not ( k_min >= temp_p.h or open_list.isempty() )
其中,判断结束条件的 open_list.isempty() 如果被满足,即open表为空,意味着无解,这点和A*及dijkstra是一样的。(当然实际操作时一般不用open表为空作为条件,而是用open表中最小的k值大于等于前面设置的超大的值时就退出,或者在搜索过程中对于那些k值超过前面设置的超大值时,直接不将其加入open表。)
判断条件的 k_min >= temp_p.h 如果被满足,则代表找到解(找到从当前点到目标点的新最短路径)了。简单来说, k_min = process_state()这句, process_state()每次都是处理k值最小的点,当open表中最小的k值k_min比当前所在的点的h值还要大的时候,说明当前这个点temp_p已经被搜索过了。
这里需要提一下h跟k究竟具体代表什么。
h值
在重规划时,h表示搜到当前这一步的时候,当前这个点到目标点的最小代价,但是它不一定是最终找到最短路径后的最小代价,因为很可能最短路径上的点还没被搜索到呢,等会搜索到比现在这一步还短的路径时,当前点h的值自然会被修改成沿着那条更短路径到终点的代价。
k值
对于初次搜索路径时,k值的意义很明显就是跟h值是等价的,两者并无区分,具体意义参考dijkstra和A*算法的实际总代价值。
对于重规划时,k值意义较为复杂,为了理解它的作用,我们必须看回代码。因为重规划实际上也是不断调用process_state的过程,所以我们去找process_state中所有有可能修改k值的地方(注意下面代码标红处):
function process_state( ):
x = get_min_k_state(oepn_list)
if x == Null then return -1
k_old = get_min_k(oepn_list)
open_list.delete(x)
x.state = "close"
# 以下为核心代码:
# 第一组判断
if k_old < x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.h<k_old and x.h> y.h + cost(y,x) then
x.parent = y
x.h = y.h + cost(x,y) # 仅仅只会修改h,不修改k
end if
end for
end if
# 第二组判断
if k_old == x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y)) # 调用了insert,可能会涉及k值变化
end if
end for
else: # 不满足k_old == x.h 那就是k_old < x.h
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) then
y.parent = x
insert(y, x.h + cost(x,y)) # 调用了insert,可能会涉及k值变化
else:
if (y.parent != x and y.h >x.h + cost(x,y)) then
x.k = x.h # 直接修改了k!!!!
insert(x, x.h) # 调用了insert,可能会涉及k值变化
else:
if (y.parent!=x and x.h>y.h+cost(y,x) and y.parent = "close" and y.h>k_old then
insert(y,y.h) # 调用了insert,可能会涉及k值变化
end if
end if
end if
end for
end if
return get_min_k(oepn_list)
可以看到稍微涉及到k值变化的也就上面几个标红的地方,其中4个都是insert函数。那么我们再来看insert函数:
function insert(state, new_h)if state.t == "new": # 将未探索过的点加入到open表时,h设置为传进来的 new_h
state.k = h_new # 因为未曾被探索过,k又是历史最小的h,所以k就是new_h
elif state.t == "open":
state.k = min(state.k, h_new) # 保持k为历史最小的h
elif state.t == "close":
state.k = min(state.k, h_new) # 保持k为历史最小的h
state.h = h_new # h意为当前点到终点的代价
state.t = "open" # 插入到open表里所以状态也要维护成open
open_list.add(state) # 插入到open表
在insert函数里,一个state的k值仅仅在传进来的参数new_h比k值更小的时候,k值才会被替换成新h值,这也合理,毕竟原论文中k的意义本身是“历史h值中最小的h值”嘛。
让我们再回到重规划时的process_state这个语境中。想一件事:我有一个地图,并且我一开始已经知道起点到终点的最短路径R(也即第一次搜索得到的结果)。可以肯定的是,对于这个最短路径R上的任何一个点来说,从这个点出发到目的地的最短路径肯定是前面说的这个最短路径R的从这个点开始的剩余部分。(反证:因为如果有更短的路,那最短路径R就不是从起点到终点的最短路径了呀,我完全可以走到这个点之后走那个更短的路径,这样肯定更短,这会出现矛盾)。
现在,我在原来地图的基础上额外增加新的障碍物,很可能①障碍物挡在了我原来的最短路径R上。这种情况下,我可能需要绕一条更长的路才能到达目标,也可能存在一条跟当前路径一样长的路,我可以走那条路,但不论怎么说,新的最短路径长度一定大于等于原本的最短路径R,绝对不可能比最短路径R还短(没理由障碍物多了反而我走的路更短吧)。也可能是②障碍物没挡住我,那我的最短路径一定不变。总结来说,发现新障碍物之后的最短路径一定比原本没有新障碍物时候的最短路径长,或者是一样长。
那么根据上面2段文字,我们知道,加入新障碍物后,某个点到目标点的最短路径长度,也即代价,一定是只能增不能减的。这说明什么?说明在重规划这个时候,执行insert函数时传进来的参数new_h一定不可能比原本的k值小,因为在第一次搜索结束时h跟k是相等的,都是最小代价,加入新障碍物后搜索过程中new_h “新代价”一定要比第一次搜索结束时的h“代价”要大,那也就是肯定比k都大。那也就是说,在重规划时,insert函数中,k值绝对不可能被更新。
说了3大段那么多,就是想说明一个事情:重规划时insert函数并不改变k值。那么返回到上面5处标红代码,我们可以看到,k值会被改变仅仅只有一个情况。那就是第二组判断中的某个条件下,直接修改k值那个地方(下面标红):
function process_state( ):
x = get_min_k_state(oepn_list)
if x == Null then return -1
k_old = get_min_k(oepn_list)
open_list.delete(x)
x.state = "close"
# 以下为核心代码:
# 第一组判断
if k_old < x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.h<k_old and x.h> y.h + cost(y,x) then
x.parent = y
x.h = y.h + cost(x,y) # 仅仅只会修改h,不修改k
end if
end for
end if
# 第二组判断
if k_old == x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y)) # 重规划过程中不修改k
end if
end for
else: # 不满足k_old == x.h 那就是k_old < x.h
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) then
y.parent = x
insert(y, x.h + cost(x,y)) # 重规划过程中不修改k
else:
if (y.parent != x and y.h >x.h + cost(x,y)) then
x.k = x.h # 唯一一个修改k的地方
insert(x, x.h) # 重规划过程中不修改k
else:
if (y.parent!=x and x.h>y.h+cost(y,x) and y.parent = "close" and y.h>k_old then
insert(y,y.h) # 重规划过程中不修改k
end if
end if
end if
end for
end if
return get_min_k(oepn_list)
关于这个标红的地方的k值究竟会怎么修改,结论是:k值一定会被变大,变得比更新前的k值更大。原因在上面也说过了,在重规划过程中,所有点的代价一定比原来的大,也即这里出现的所有h值肯定都比第一次搜索结束后的k值大,那x.k=x.h这句,x.h肯定是比x.k大的。
那么什么时候一个点的k值会被修改呢?先告诉你结论:当我们找到了从这个点到目标点的,考虑了新障碍物之后的,新的最短路径newR后,这个点的k值会标修改成更大,并且这个修改后的k值代表了沿着新的最短路径newR,这个点到目标点的代价 / 实际距离。至于原因我们将在后面详解process_state中各判断条件时讨论。
综上所述,某个点的k值在重规划时的意义是:????
回到前面讨论,k_min >= temp_p什么意思