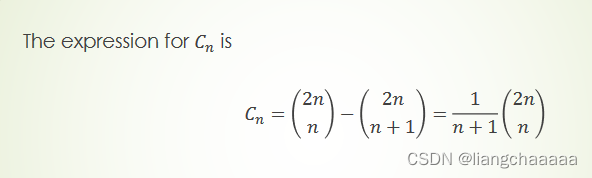Catalan numbers(卡特兰数)
先通过平衡括号引入卡特兰数序列的概念



1,2,5,14,...,这些数构成了卡特兰数序列,分别代表一共有i个括号时,括号排列构成的合法方案数【从左到右如果所有括号都能依次配对即是合法的,如 “())(” 是不合法的】
Monotonic lattice paths(路径记数问题)

规则:在一个n*n的方格图中,从左上角的点走到右下角的点,只能向右走或者向下走,并且只能在正方形对角线右上部分,不能越过对角线走(例如在3*3的图中,下图就越过了对角线)


巧合的是,非降路径方案数和卡特兰数是一样的。
因为非降路径方案数可以映射成一个平衡括号问题,向右走映射成左括号,向下走映射成右括号。n*n的方格图,有n个左括号和n个有括号,可以构成n对括号;由(x,y)在y = -x+n右上侧推出x+y>=n,进而推出x>=n-y(其中x为实际向右走的步数,n-y为实际向下走的步数),这也保证了括号一定匹配的上,不会出现左到右顺序遍历时有右括号而无左括号匹配的问题。
Polygon triangulation(三角剖分)
三角剖分在CG中的作用:
在计算机图形学中,通常使用多边形网格来表示三维物体表面,而三角剖分就是将多边形划分成若干个三角形的过程。三角剖分可以将原始几何体离散化为一系列三角形,并根据需要进行进一步的计算和处理。其中,三角剖分质量的好坏将直接影响到后续基于这些数据进行的渲染、物理模拟或者其他算法的效果质量和速度。
同时,三角剖分也是很多计算机图形学算法的核心部分,例如曲面重建、形态分析、三维扫描等。在这些应用中,三角剖分不仅是将复杂的几何对象进行离散化的手段,还充当了连接各种计算机图形学算法所需的输入数据的媒介。因此,三角剖分在计算机图形学中具有广泛的应用。

求的是对凸多边形通过不相交的对角线切分成三角形的不同切分方案数
巧合的是,划分成n个三角形的方案数和n对平衡括号的方案数也是一样的
具体怎么映射......我也不懂
递归数列

n为多边形的边数,
为卡特兰数通项
具体解释:选定一条边,再选除了选定边的两点外的一点,将多边形分成三块区域,而边和点构成的三角形两边的区域分割方案数也是卡特兰数
例子:
第一幅图中,白色的为七边形,方案数为
第二幅图中,黄色的为三角形,方案数为
,绿色的为六边形,方案数为
,

生成函数求卡特兰数序列的通项公式