✨博主:命运之光
🦄专栏:算法修炼之练气篇
🍓专栏:算法修炼之筑基篇
✨博主的其他文章:点击进入博主的主页
前言:学习了算法修炼之练气篇想必各位蒟蒻们的基础已经非常的扎实了,下来我们进阶到算法修炼之筑基篇的学习。筑基期和练气期难度可谓是天差地别,懂得都懂,题目难度相比起练气期的题目难度提升很多,所以要是各位蒟蒻小伙伴们看不懂筑基期的题目可以在练气期多积累积累,练气期的题目也会不断更新,大家一定要把基础打牢固了再来看筑基期的题目哈,这样子也可以提高大家的学习效率,一举两得,加油(●'◡'●)🎉🎉

目录
✨详解文字版(01背包,完全背包,多重背包)
🍓01背包问题
🍓完全背包问题
🍓多重背包问题
✨01背包问题(经典)
🍓小明的背包1
🍓解法一:二维dp数组
🍓解法二:一维dp数组
✨完全背包问题(经典)
🍓小明的背包2
🍓一维dp数组
🍓一维dp数组关键步骤(记忆)
🍓01背包和完全背包两个对比(重要)
😭总结就一个公式(超级无敌重要)
🍓🍓01背包总结
🍓🍓完全背包总结
✨多重背包问题(经典)
🍓小明的背包3
🍓重要步骤
✨详解文字版(01背包,完全背包,多重背包)
光看文字我感觉,很难理解背包问题,关键还是要看看底下的经典例题,看完差不多就可以了,问题不好理解,大家加油哈(●'◡'●)
背包问题的理解和解法。这三种问题分别是:
- 01背包问题:每种物品只能选择一次,求最大价值。
- 完全背包问题:每种物品可以选择无限次,求最大价值。
- 多重背包问题:每种物品有一个选择上限,求最大价值。
这三种问题都可以用动态规划的思想来解决,关键是找到状态转移方程。下面我就分别介绍一下这三种问题的思路和代码实现。(看不懂的话可以直接跳到例题,看例题我感觉就能直接理解,不用文字这么的啰嗦哈哈啊哈🤭)
🍓01背包问题
01背包问题是所有背包问题的基础,之后的问题都可以在此基础之上变化,所以一定要理解清楚。尤其是对待不同问题,找出状态转移方程是解题的关键。
假设有N件物品和一个容量为V的背包。第i件物品的体积是v[i],价值是w[i]。我们用f[i][j]表示前i件物品恰好放入一个容量为j的背包中的最大价值。那么我们可以得到如下的状态转移方程:
f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i])
这个方程的意思是,对于第i件物品,我们有两种选择:放或者不放。如果不放,那么前i件物品的最大价值就等于前i-1件物品的最大价值;如果放,那么前i件物品的最大价值就等于前i-1件物品在剩余空间j-v[i]中的最大价值加上第i件物品的价值。我们取这两种情况中较大的一个作为f[i][j]的值。
根据这个方程,我们可以用二维数组来存储f[i][j]的值,并从小到大遍历所有可能的状态。最终答案就是f[N][V]。
🍓下面是用C++实现的代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1001; // 物品数量和背包容量的上限
int f[N][N]; // 存储状态转移方程的结果
int v[N]; // 存储每件物品的体积
int w[N]; // 存储每件物品的价值
int main() {
int n, V; // 物品数量和背包容量
cin >> n >> V;
for (int i = 1; i <= n; i++) {
cin >> v[i] >> w[i]; // 输入每件物品的体积和价值
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= V; j++) {
f[i][j] = f[i-1][j]; // 不放第i件物品
if (j >= v[i]) { // 如果能放得下第i件物品
f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]); // 取放和不放中较大的一个
}
}
}
cout << f[n][V] << endl; // 输出最大价值
return 0;
}
🍓完全背包问题
完全背包问题与01背包问题非常相似,只是每种物品可以选择无限次而已。这样一来,我们的状态转移方程就有所变化:
f[i][j] = max(f[i-1][j], f[i][j-v[i]] + w[i])
这个方程的意思是,对于第i件物品,我们有两种选择:放或者不放。如果不放,那么前i件物品的最大价值就等于前i-1件物品的最大价值;如果放,那么前i件物品的最大价值就等于当前物品在剩余空间j-v[i]中的最大价值加上第i件物品的价值。注意这里和01背包问题的区别,因为可以放多次,所以是f[i][j-v[i]]而不是f[i-1][j-v[i]]。
根据这个方程,我们仍然可以用二维数组来存储f[i][j]的值,并从小到大遍历所有可能的状态。最终答案仍然是f[N][V]。
🍓下面是用C++实现的代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1001; // 物品数量和背包容量的上限
int f[N][N]; // 存储状态转移方程的结果
int v[N]; // 存储每件物品的体积
int w[N]; // 存储每件物品的价值
int main() {
int n, V; // 物品数量和背包容量
cin >> n >> V;
for (int i = 1; i <= n; i++) {
cin >> v[i] >> w[i]; // 输入每件物品的体积和价值
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= V; j++) {
f[i][j] = f[i-1][j]; // 不放第i件物品
if (j >= v[i]) { // 如果能放得下第i件物品
f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]); // 取放和不放中较大的一个
}
}
}
cout << f[n][V] << endl; // 输出最大价值
return 0;
}🍓多重背包问题
多重背包问题的描述是这样的:有n种物品和一个容量为m的背包,每种物品有一定的重量w[i]和价值v[i],还有数量限制num[i],即每种物品最多只能放num[i]个。问如何选择放入背包的物品,使得背包内物品的总价值最大,且不超过背包的容量。🤔
这个问题看起来很复杂,但其实我们可以用一些技巧来简化它。首先,我们可以把每种物品看成是若干个01背包问题中的物品,即把第i种物品分成num[i]个单独的物品,每个物品的重量和价值都是w[i]和v[i]。这样我们就把多重背包问题转化成了一个01背包问题。😎
然后,我们可以用一个二维数组dp[i][j]来表示从前i个物品中选择若干个放入容量为j的背包时能获得的最大价值。我们可以用一个循环来遍历所有的物品,对于每个物品,我们又用一个循环来遍历所有可能的背包容量,然后根据放或不放这个物品来更新dp[i][j]的值。具体来说,如果不放这个物品,那么dp[i][j]就等于dp[i-1][j],即前i-1个物品放入容量为j的背包时能获得的最大价值;如果放这个物品,那么dp[i][j]就等于dp[i-1][j-w[i]]+v[i],即前i-1个物品放入容量为j-w[i]的背包时能获得的最大价值加上当前物品的价值。我们要在这两种情况中取较大的那个作为dp[i][j]的值。👍
最后,我们可以输出dp[n][m]作为最终答案,即从n种物品中选择若干个放入容量为m的背包时能获得的最大价值。这就是多重背包问题的解法。🎉
✨01背包问题(经典)
🍓小明的背包1

🍓解法一:二维dp数组
#include<bits/stdc++.h>
using namespace std;
int dp[1005][1005],w[1005],v[1005];
int main()
{
//经典的01背包问题需要记忆
int n,m;
int i,j;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(j<w[i])
{
dp[i][j]=dp[i-1][j];//记忆
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);//记忆
}
}
}
cout<<dp[n][m];
return 0;
}🍓解法二:一维dp数组
#include<bits/stdc++.h>
using namespace std;
int dp[1005],w[1005],v[1005];
int main()
{
//经典的01背包问题需要记忆
int n,m;
int i,j;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(i=1;i<=n;i++)
{
for(j=m;j>=1;j--)//--j和j--不影响,01背包是逆序
{
if(j>w[i])
{
dp[j]=max(dp[j-1],dp[j-w[i]]+v[i]);
}
}
}
cout<<dp[m];
return 0;
}🍓用这个dp[j]=max(dp[j],dp[j-w[i]]+v[i])
#include<bits/stdc++.h>
using namespace std;
int dp[1005],w[1005],v[1005];
int main()
{
//经典的01背包问题需要记忆
int n,m;
int i,j;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(i=1;i<=n;i++)
{
for(j=m;j>=1;j--)//--j和j--不影响,01背包是逆序
{
if(j>=w[i])
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[m];
return 0;
}下面是需要记忆知识点(01背包问题中的推到公式需要记忆)
🍓二维dp数组
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(j<w[i])
{
dp[i][j]=dp[i-1][j];//记忆
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);//记忆
}
}
}🍓一维dp数组(重要)
for(i=1;i<=n;i++)
{
for(j=m;j>=1;j--)//--j和j--不影响,01背包是逆序
{
if(j>=w[i])
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
} 
✨完全背包问题(经典)
🍓小明的背包2

🍓一维dp数组
#include<bits/stdc++.h>
using namespace std;
int dp[1005],w[1005],v[1005];
int main()
{
//经典的完全背包问题需要记忆
int n,m;
int i,j;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[m];
return 0;
}🍓一维dp数组关键步骤(记忆)
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
} 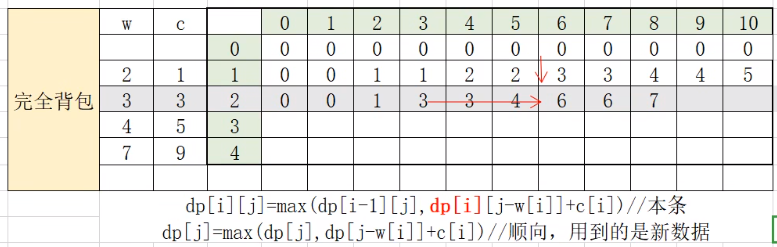
🍓01背包和完全背包两个对比(重要)


😭总结就一个公式(超级无敌重要)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
其中01背包是逆向推到,完全背包是正向推到
🍓🍓01背包总结
for(i=1;i<=n;i++)
{
for(j=m;j>=1;j--)//--j和j--不影响,01背包是逆序
{
if(j>=w[i])
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
} 🍓🍓完全背包总结
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)//重要点,j=w[i];j<=m;j++
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
} ✨多重背包问题(经典)
理解了上面的01背包问题和多重背包问题就很好理解多重背包问题了
🍓小明的背包3

#include<bits/stdc++.h>
using namespace std;
int dp[205],w[205],vi[205],s[205];
int main()
{
//经典的多重背包问题
int n,v;
int i,j;
cin>>n>>v;
for(i=1;i<=n;i++)
{
cin>>w[i]>>vi[i]>>s[i];
}
for(i=1;i<=n;i++)
{
for(j=v;j>=1;j--)
{
for(int k=0;k<=s[i]&&j>=k*w[i];++k)
{
//从01背包的状态转移方程式,去增加i个物品拿k个循环
dp[j]=max(dp[j],dp[j-k*w[i]]+k*vi[i]);
}
}
}
cout<<dp[v];
return 0;
}🍓重要步骤
🍓就是在01背包的基础上加上K循环的约束条件和dp[j]=max(dp[j],dp[j-k*w[i]]+k*vi[i])
for(i=1;i<=n;i++)
{
for(j=v;j>=1;j--)//01背包的基础上他这个也是逆向的
{
for(int k=0;k<=s[i]&&j>=k*w[i];++k)
{
//从01背包的状态转移方程式,去增加i个物品拿k个循环
dp[j]=max(dp[j],dp[j-k*w[i]]+k*vi[i]);
}
}
}